Алгоритм метода искусственного базиса

Вспомогательная задача ЛП.

Симплекс-метод применяется для решения специальных задач ЛП, представленных в виде: 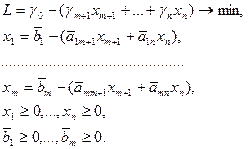(2.6)

Характерная особенность задачи (2.6) - известное базисное допустимое решение

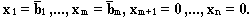
Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо эту задачу привести к виду (2.6), т.е. выделить начальный допустимый базис. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса. Рассмотрим каноническую задачу ЛП, которая не является СЗЛП (в ней нет выделенного базиса)

Приводим задачу ЛП к канонической форме

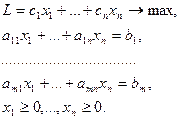(2.7)

причем

(если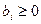, то умножаем i-ю строку ограничений на -1)

Вспомогательной задачей ЛП (ВЗЛП) называется задача вида

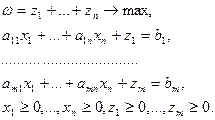(2.8)

Переменные вспомогательной задачи

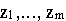образуют базис ВЗЛП и называются искусственными.

Рассмотрим свойства вспомогательной задачи.

Свойство 1.

ВЗЛП легко может быть сведена к допустимой СЗЛП. Действительно, ВЗЛП имеет очевидное базисное допустимое решение

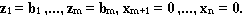
Для того, чтобы сделать вспомогательную задачу специальной, достаточно целевую функцию выразить через свободные переменные

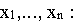
Свойство 2.

ВЗЛП всегда имеет решение причем оптимальное значение целевой функции

Доказательство.

Так как ВЗЛП имеет допустимое решение

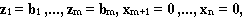
то допустимая область ВЗЛП не пустая.

Так как

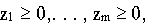
то целевая функция

на любом допустимом решении.

Таким образом, целевая функция 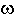ограничена снизу нулем на непустом допустимом множестве, следовательно ВЗЛП разрешима всегда и оптимальное значение целевой функции

Свойство доказано.

Если КЗЛП имеет допустимые решения, то существует эквивалентная ей СЗЛП, которая может быть получена из оптимальной симплексной таблицы ВЗЛП.

Доказательство.

КЗЛП имеет допустимые решения, тогда по критерию существования планов КЗЛП имеем 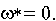Рассмотрим соответствующую оптимальную симплекс-таблицу ВЗЛП.

Возможны два случая.

Случай 1. В базисе оптимальной симплекс-таблице ВЗЛП отсутствуют искусственные переменные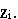

Симплекс-таблица имеет вид

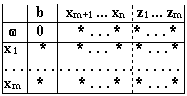
Возьмем ту часть таблицы которая не содержит

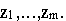
Равенства соответствующие оставшейся части таблицы не нарушатся, поскольку исключили небазисные нулевые искусственные переменные

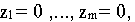
(или фактически вернулись к исходной системе уравнений без искусственных переменных). В результате имеем систему уравнений относительно переменных

с выделенным базисом

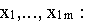
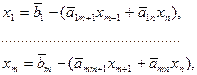(2.9)

Эта система эквивалентна исходной КЗЛП, так как получена из нее с помощью гауссовских преобразований.

Выражая целевую функцию исходной задачи

через небазисные переменные

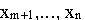получим СЗЛП.

Случай 2. В базисе оптимальной симплекс-таблице находятся искусственные переменные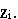

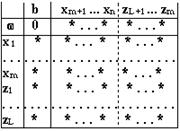
Как и в случае 1 берем ту часть таблицы, которая не содержит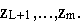

Равенства при этом не нарушаются, как и в случае 1.

Затем вычеркиваем нулевые строки (если такие есть) и с помощью гауссовских преобразований заменяем в базисе переменные 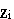, i=1,..., L переменными

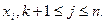
Шаг 1. Приводим задачу ЛП к каноническому виду с неотрицательными правыми частями 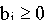, i=1,..., m.

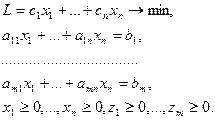
Шаг 2. Строим вспомогательную задачу ЛП

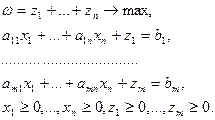
и приводим ее к специальному виду. Для этого целевую функцию выражаем через небазисные переменные.

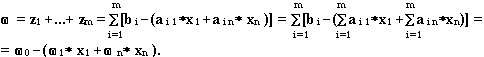
Шаг 3. Решаем ВЗЛП симплекс-методом.

Шаг 4. Если 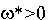, то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается.

Шаг 5. Если 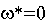, то строим СЗЛП для исходной задачи на основе оптимальной симплек-таблицы ВЗЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.

Тема 4. Транспортная задача.

Дата добавления: 2014-01-15