Постановка задачи. Составление опорного плана

Метод потенциалов.

Составление опорного плана.

Постановка задачи.

Транспортная задача ставится следующим образом: имеется m пунктов отправления_, в которых сосредоточены запасы каких-то грузов. Имеется n пунктов назначения подавшие заявки соответственно на груза. Известны стоимости р _{i j} перевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Все числа р _{i j ,} образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок (откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна. Далее, предполагается, что

(1)

где b_i есть количество продукции, находящееся на складе i, и a_j – потребность потребителя j.

Замечание. Если 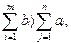то количество продукции, равное 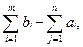остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью 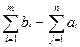и положим транспортные расходы p_{i,n +1} равными 0 для всех i.

Если 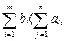то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.

Обозначим через x_ij количество продукции, поставляемое со склада i потребителю j. В предложении (1) нам нужно решить следующую задачу (математическая модель транспортной задачи):

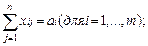(2)

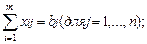
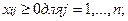
Транспортную задачу мы можем характеризовать транспортной таблицей и таблицей издержек:

	а1	…	аn
b1 bm	.
	.
		.
			.
				.
					.
p11	…	p1n
.		.
.		.
.		.
pm1	…	pmn

Допустимый план перевозок будем представлять в виде транспортной таблицы:

	а1	…	аn
b . . . bm		…
.		.
.		.
.		.
	…

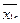
Cумма элементов строки i должна быть равна b_i, а сумма элементов столбца j должна быть равна a_j, и все 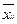должны быть неотрицательными.

+х₂₅+х₃₅=5;

х_ij 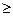0 для i

Пример 1.

Мы получаем следующую задачу:

х₁₁+х₁₂+х₁₃+х₁₄+х₁₅=15,

х₂₁+х₂₂+х₂₃+х₂₄+х₅₅=15,

х₃₁+х₃₂+х₃₃+х₃₄+х₃₅ =20,

х₁₁ +х₂₁+х₃₁=20,

х₁₂+х₂₂+х₃₂=5,

х₁₃+х₂₃+х₃₃=10,

х₁₄ +х₂₄+х₃₄

х₁₅ = 1,2,3; j = 1,2,3,4,5;

К_min=5х₁₁+6х₁₂+3х₁₃+5х₁₄+9х₁₅+6х₂₁+4х₂₂+7х₂₃+3х₂₄+5х₂₅+2х₃₁+5х₃₂+3х₃₃+х₃₄+8х₃₅;

Такие задачи целесообразно решать при помощи особого варианта симплекс-метода – так называемого метода потенциалов.

Все транспортные задачи имеют оптимальное решение. Если все значение a_j и b_i в условиях транспортной задачи целочисленные, то переменные x_ij во всех базисных решениях (а так же и в любом оптимальном базисном решении) имеют целочисленные значения.

Дата добавления: 2014-01-15