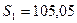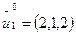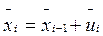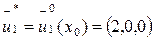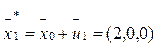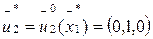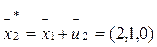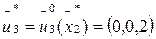КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исходные данные для примера
|
|
|
|
Выбор состава оборудования для технологической линии.
Есть технологическая линия, то есть цепочка, последовательность операций.
На каждую операцию можно назначить оборудование только каго-то одного вида, а оборудования, способного работать на данной операции, - несколько видов.
| i | ||||||||
| j | ||||||||
| ||||||||
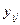
| ||||||||
|
|
Стоимость сырья
Расходы, связанные с использованием единицы оборудования j-го типа на i-ой операции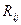 Производительности, соответственно, по выходу и входу
Производительности, соответственно, по выходу и входу 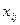 и
и 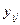 для j-го типа оборудования, претендующего на i-ую операцию.
для j-го типа оборудования, претендующего на i-ую операцию.
Решение:
Для того, чтобы решить данную задачу методом динамического программирования введем следующие обозначения:
N = 3 – число шагов.
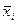 - Технологическая линия.
- Технологическая линия.
|
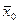 = (0,0,0)
= (0,0,0)
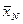 = ()
= ()
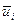 – выбор оборудования для i-ой операции.
– выбор оборудования для i-ой операции.
Ui – область допустимых УВ на i-м шаге.
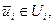 т.е.
т.е.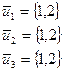
Wi – оценка минимальной себестоимости, полученная в результате реализации i-го шага.
S – функция общего выигрыша т. е. минимальная себестоимость.
| ||||||
|
| |||||
вектор – функция, описывающая переход системы из состояния в состояние 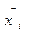 под действием УВ.
под действием УВ.
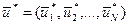 - вектор УВ на i-ом шаге, обеспечивающий переход системы из состояния xi-1 в состояние xi, т.е. оптимальный выбор оборудования за N шагов.
- вектор УВ на i-ом шаге, обеспечивающий переход системы из состояния xi-1 в состояние xi, т.е. оптимальный выбор оборудования за N шагов.
Si+1(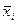 ) – максимальный выигрыш (в нашем случае минимальная себестоимость), получаемый при переходе из любого состояния
) – максимальный выигрыш (в нашем случае минимальная себестоимость), получаемый при переходе из любого состояния 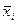
 в конечное состояние
в конечное состояние 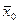 при оптимальной стратегии управления начиная с (k+1)-го шага.
при оптимальной стратегии управления начиная с (k+1)-го шага.
S1(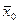 ) – максимальный выигрыш, получаемый за N шагов при переходе системы из начального состояния
) – максимальный выигрыш, получаемый за N шагов при переходе системы из начального состояния 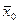 в конечное
в конечное 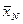 при реализации оптимальной стратегии управления
при реализации оптимальной стратегии управления 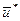 . Очевидно, что S = S1(
. Очевидно, что S = S1(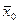 ), если
), если 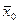 = 0.
= 0.
Запишем вектора допустимых значений
|
Запишем вектора допустимых управляющих воздействий
|
|
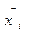 под действием УВ.
под действием УВ.
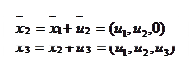 |
|
| |||
| |||
1) Обратный проход
Для i=3
Учитывая то, что этот шаг у нас последний и следующей операции
|
|
возьмем стоимость сырья
| |||
| |||
при 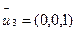 =
=
| |||
| |||
при 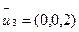 =
=
|
|
т. е.
Для i=2
|
| |||
| |||
при 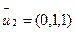 =
=
| |||
|
при 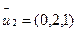 =
=
|
при 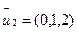 =
=
| ||||
| ||||
| ||||
при 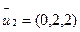 =
=
| |||
| |||
т. е.
Для i=1
| |||||
| |||||
| |||||
при 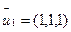 =
=
| |||
| |||
при 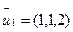 =
=
|
|
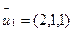 =
=
| |||
| |||
при 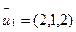 ==
==
| |||
| |||
при 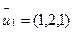 =
=
| |||
| |||
при 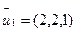 =
=
| |||
| |||
при 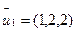 =
=
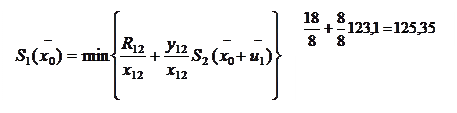 |
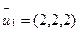
|
|
2)
|
Учитывая то, что и 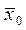 = (0,0,0) имеем
= (0,0,0) имеем
|
|
|
|
|
|
Таким образом оптимальный выбор состава оборудования технологической линии предполагает следующее:
На 1-ую операцию назначим оборудование 2-го вида
На 2-ую операцию назначим оборудование 1-го вида
На 3-ью операцию назначим оборудование 2-го вида
Оценка минимальной себестоимости составит 105,5.
Тема 2. Задача инвестирования.
Предположим, что в начале каждого из следующих n лет необходимо сделать инвестиции P1, P2,…, Pn соответственно. Вы имеете возможность вложить капитал в два банка: первый банк выплачивает годовой сложный процент r1, а второй - r2. Для поощрения депозитов оба банка выплачивают новым инвесторам премии в виде процента от вложенной суммы.
Премиальные меняются от года к году, и для і-ого года равны qi1 и qi2 в первом и втором банках соответственно. Они выплачиваются к концу года, на протяжении которого сделан вклад, и могут быть инвестированы в один из двух банков на следующий год. Это значит, что лишь указанные проценты и новые деньги могут быть инвестированы в один из двух банков. Размещенный в банке вклад должен находится там до конца рассматриваемого периода. Необходимо разработать стратегию инвестиции на следующие n лет.
Элементы модели динамического программирования следующие:
Этап і представляется порядковым номером года і, і=1,2,...n
Вариантами решения на і-м этапе (для і-ого года) являются суммы li и 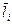 инвестиций в первый и второй банк соответственно.
инвестиций в первый и второй банк соответственно.
Состоянием xi на і-м этапе является сумма денег на начало і-ого года, которые могут быть инвестированы.
Заметим, что по определению =xi-li. Следовательно,
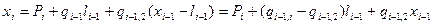
где і=2,3,…n, x1=P1. Сумма денег xi, которые могут быть инвестированы, включает лишь новые деньги и премиальные проценты за инвестиции, сделанные на протяжении (і-1)-го года.
Пусть fi(xi)- оптимальная сумма инвестиций для интервала от і-го до n-го года при условии, что в начале і-го года имеется денежная сумма xi. Далее обозначим через si накопленную сумму к концу n-го года при условии, что li и (xi-li)-объемы инвестиций на протяжении і-го года в первый и второй банк соответственно. Обозначая 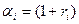 , і=1,2, мы можем сформулировать задачу в следующем виде.
, і=1,2, мы можем сформулировать задачу в следующем виде.
Максимизировать z=s1+s2+…+sn, где
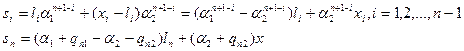
Так как премиальные за n-й год являются частью накопленной денежной суммы от инвестиций, в выражения для sn добавлены qn1 и qn2.
Итак, в данном случае рекуррентное уравнение для обратной прогонки в алгоритме динамического программирования имеет вид
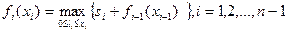
где xi+1 выражается через xi в соответствии с приведенной выше формулой, а fn+1(xn+1)=0.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 456; Нарушение авторских прав?; Мы поможем в написании вашей работы!

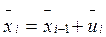
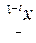
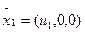
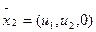

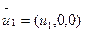
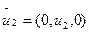
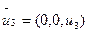
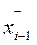
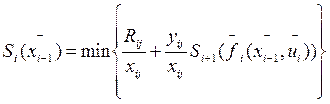
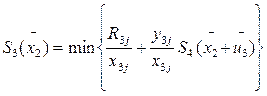
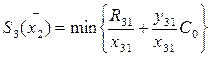
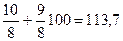
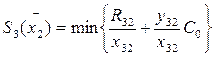
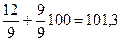
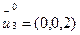
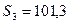
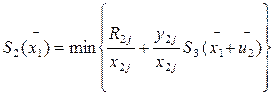
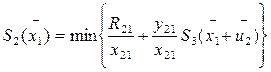
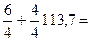 115,2
115,2
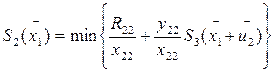
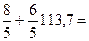 138,04
138,04
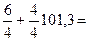 102,8
102,8
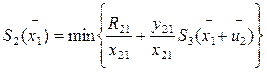

 123,1
123,1
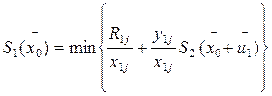
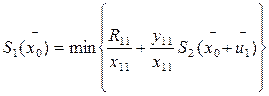
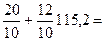 140,2
140,2
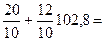 125,3
125,3
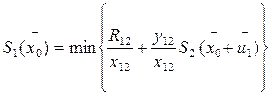
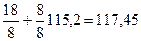 125,3
125,3
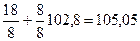 125,3
125,3
 125,3
125,3
 125,3
125,3
 125,3
125,3