Математическое описание разрабатываемой модели

На вход системы из N станций поступает поток заявок с заданными (экспоненциальным или нормальным) законом распределения времени прихода, интенсивностью входного потока l и, при нормальном распределении, коэффициентом вариации nl. Каждая станция рассматривается, как одноканальная СМО с неограниченной очередью. На каждой станции задано среднее время обслуживания 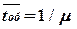и, при нормальном распределении, коэффициент вариации nm. На выходе станций поток заявок может ветвиться, также может происходить отбраковка заявок. Это изменяет интенсивность входного потока на последующих станциях.

При имитационном моделировании поэтапно имитируется (с использованием генератора случайных чисел) весь описанный процесс: моделируются входной поток и потоки обслуживаний, имитируются процессы ветвления и объединения потоков, а также процесс отбраковки заявок.

Расчетно-формульная модель такой системы может рассматриваться только в случае, когда существуют финальные вероятности. Для таких СМО финальные вероятности существуют только тогда, когда станции не перегружены, т. е для всех станций выполняется условие ()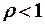

Дата добавления: 2014-01-15