Формулировка задачи

Построить модель СМО и исследовать поведение характеристик её эффективности.

Описание системы:

Имеется двухканальная СМО с отказами, на которую поступает два произвольных потока заявок. Поток I имеет интенсивность l₁. Поток II имеет интенсивность l₂ (будем кратко именовать заявки этих потоков: Заявки I и ЗаявкиII). Заявки I имеют пред Заявками II приоритет, состоящий в том, что если Заявка I приходит в систему, когда все каналы заняты и хотя бы один из них обслуживает Заявку II, то пришедшая Заявка I «вытесняет» (выгоняет) Заявку II, становится на её место, а та покидает систему необслуженной. Если Заявка I приходит в момент, когда оба канала обслуживают Заявки I, то она получает отказ и покидает СМО. Заявка II получает отказ, если она приходит в систему в момент, когда оба канала заняты (безразлично какими заявками).

Данные для варианта: l₁ =3, l₂ =1, m₁ =2, m₂ =1. Теоретическое представление задачи.

На двухканальную СМО поступают заявки двух простейших потоков.

Простейшим потоком называется поток, обладающий следующими свойствами:

1. стационарность;

2. ординарность;

3. отсутствие последействия.

Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной t зависит только от длины участка и не зависит от того, где именно на оси времени расположен этот участок.

Поток событий называется ординарным, если вероятность попадания на элементарный участок Dt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Ординарность означает, что поток прореженный, т.е. между любыми двумя событиями есть временной интервал.

Поток событий называется потоком без последействия, если для любых, не перекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Это означает, что заявки попадают в систему не зависимо друг от друга.

Интенсивность поступления заявок 1-го потока - l1. Интенсивность поступления заявок 2-го потока - l2. Простейшие потоки поступления заявок характеризуются показательным законом распределения. Тогда интервал времени поступления заявок 1-го потока представляет собой случайную величину с одним и тем же распределением вероятностей F (t).

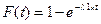, (1) где l1>0 – постоянная.

Плотность распределения показательного закона задается формулой:

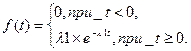
где l1>0, - интенсивность поступления заявок 1-го потока.

Аналогично, интервал времени поступления заявок 2-го потока представляет собой случайную величину с одним и тем же распределением вероятностей F(t).

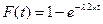, (1) где l2>0 – постоянная.

Плотность распределения показательного закона задается формулой:

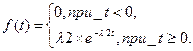
где l2>0, - интенсивность поступления заявок 2-го потока.

Необходимо также учесть, что моделируемая система массового обслуживания является СМО с отказами и с абсолютным приоритетом. Т.е. заявки 1 имеют перед заявками 2 приоритет, состоящий в том, что если заявка 1 приходит в систему, когда все каналы заняты и хотя бы один из них обслуживает заявку 2, то пришедшая заявка 1 вытесняет заявку 2, становится на ее место, а та покидает систему не обслуженной. Если заявка 1 приходит в систему в момент, когда оба канала обслуживают заявку 1, то она покидает СМО. Заявка 2 получает отказ, если она приходит в систему в момент, когда оба канала заняты, безразлично какими заявками.

Длительность обслуживания заявок 1-го и 2-го потока также представляют собой случайные величины, подчиняющиеся показательному закону распределения. Интенсивность обслуживания аявок 1-го потока - m1. Интенсивность обслуживания заявок 2-го потока - m2. Длительность обслуживания заявок 1-го потока представляет собой случайную величину с одним и тем же распределением вероятностей F (t).

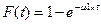, (1) где m1>0 – постоянная.

Плотность распределения показательного закона задается формулой:

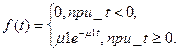
где m1>0, - интенсивность обслуживания заявок 1-го потока.

Аналогично, длительность обслуживания заявок 2-го потока представляет собой случайную величину с одним и тем же распределением вероятностей F(t).

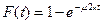, (1) где m2>0 – постоянная.

Плотность распределения показательного закона задается формулой:

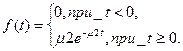
где m2>0, - интенсивность обслуживания заявок 2-го потока.

В рассматриваемой задаче СМО имеет 2 входа, на один из которых поступает случайный поток Заявок I, на другой вход - поток Заявок II.

Дата добавления: 2014-01-15