Максиминный критерий Вальда

Согласно этому критерию игра с природой ведется как игра с разум­ным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оп­тимальной считается стратегия, при которой гаранти­руется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой».

Для каждой операции а_i, i = 1, 2,..., m, находим наихудший исход,

. (3а)

Затем определяется то значение i₀, при котором величина 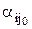максимальна,

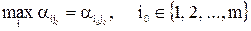. (3в)

Принимаемое решение – выбор наилучшей операции 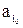из множества исходных (1). Равенства (3а), (3в) можно объединить в одно

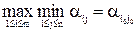. (4)

Рассмотренная операция максимин соответствует лучшему из худших исходов. Если руководствоваться этим критерием, олицетво­ряющим «позицию, крайнего пессимизма», надо, всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Критерий максимина является чисто перестраховочным, поскольку природа не может быть сознательным противником. Очевидно, такой подход - естественный для того, кто очень боится проиграть, - не является единственно возмож­ным, но как крайний случай он заслуживает рас­смотрения. Максиминную операцию использует только крайний пессимист, не желающий идти ни на какой риск. Обычно такие люди довольствуются малым и предпочитают спокойную жизнь. Критерий минимакса сожалений Сэвнджа.

Этот критерий — тоже крайне пессимистический, но при вы­боре оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска (сожаления) в наихудших условиях минимальна. Сожаление (риска) в ТПР – потери в результате упущенных возможностей.

Пусть природа находится в состоянии Q_s найдем максимальный элемент s-го столбца табл. 1,

.

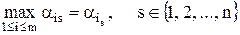Мера сожаления определяется как разность:

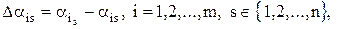
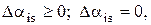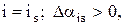где если если 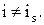Тогда при состоя­нии природы Q_s лучшей операцией является 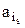: для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожа­ление для каждой операции a_i, i=1,2,…, m, при любом состояния природы Q_s, s=1,2,…, n. Матрица сожалений представлена в табл. 2.

Для принятия решения к табл. 2 применяется критерий минимакса (minmax): для каждой операции a_i, i=1,2,…, m, находится наибольшее со­жаление,

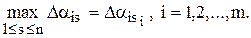
Таблица 2

Qj ai	Q1	Q2	…	Qn
a1	Da11	Da12	…	Da1n
a2	Da21	Da22	…	Da2n
…	…	…	…	…
am	Dam1	Dam2	…	Damn

Затем среди членов последовательности 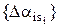, i=1,2,…, m, s = 1,2,…, n, находится минимальный

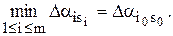
Последние два равенства соединим в одно:

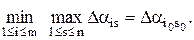
Принимаемое решение – наилучшая операция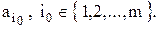

Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь пони­мается по-другому.

2.3. Критерий равновозможных состояний.

По этому критерию выбирается та операция a_i0, для которой сумма полезностей

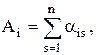
максимальна,

.

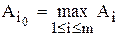Решение конкретной задачи

Рассмотрим на конкретном примере принятие решений по трем описанным критериям. Пусть m=3, n=2, и матрица полезностей представлена в табл. 3.

Таблица 3 Таблица 4

Qs ai	Q1	Q2		Qs ai	Q1	Q2
a1				a1
a2				a2
a3				a3

Например, a_i – i-ый вариант технологического процесса для изготовле­ния некоторых изделий, Q₁ – возникновение дефицита в ближайшие два года на сырье, из которого изготовляются детали, Q₂ – отсутствие такого дефицита.

1. Применяя операцию максимина, получим

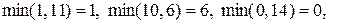
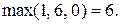
Максиминной операцией является операция а₂, гарантирующая 6 единиц полезности.

2. Для использования критерия минимакса сожалений необходимо для данных табл. 3 найти матрицу сожалений. Сначала находим максимальный элемент каждого столбца этой таблицы:

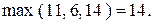
Тогда матрица сожалений примет вид, представленный в табл. 4. Применяя к данным этой таблицы критерий минимакса, получим:

max(9, 3) = 9, max(0, 8) = 8, max(10, 0) = 10, min(9, 8, 10) = 8.

Следовательно, операцией, соответствующей минимаксу сожалений, является операция а₂.

По критерию равновозможных состояний для данных табл. 3 имеем:

А_i = 1+11 = 12, A₂ = 10+6 = 16, A₃ = 0+14 = 14, .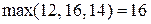

Значит, оптимальной операцией по критерию равновозможных состояний при­роды является операция а₂. В рассмотренном примере все три критерия дали один и тот же ответ: операция а₂ является оптимальной, она гарантирует 6 ед. полезности.

Если выбрать операцию а1, то в случае везения получим 11 ед. полезности, а в случае невезения – всего 1 ед. полезности. Если выбрать опера­цию а3, то в случае везения имеем 14 ед. полезности, а в случае невезения – 0 ед. полезности. Операция а2 гарантирует наибольшую полезность, 6 ед. Конкурирующие операции а1 и а3 гарантируют меньшие полезности: 1 ед. и 0 ед., соответственно.

Принятие решений в условиях риска

Самый простой случай неопределен­ности — т.н. «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности. Тогда естественно выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально.

Ситуация ПР в условиях риска возникает в случаях, когда известны ап­риорные вероятности состояний природы

р(Q₁), р(Q₂), …, р(Q_n),

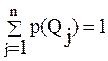. (5)

Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции а_i находят взве­шенные суммы полезностей

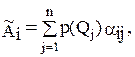i=1,2, …, m, (6)

и выбирают в качестве наилучшей ту операцию 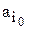, для которой взвешен­ная сумма полезностей в (6) максимальна,

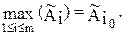
Любопытно отметить, что та же стратегия, кото­рая обращает в максимум средний выигрыш, обраща­ет в минимум в средний риск. Так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно В то же оптимальное решение.

Пусть в рассмотренном выше примере р(Q₁)=0.25, р(Q₂)=0.75.

По данным табл. 3 имеем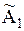= 1×0.25 + 11×0.75 = 8.5,

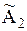= 10×0.25 + 6×0.75 = 7.0,

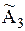= 0×0.25 + 14×0.75 = 10.5,

max (8.5; 7.0; 10.5) = 10.5.

Следовательно, наилучшей операцией является операция а₃, если р(Q₁)=0.25, р(Q₂)=0.75. Но при других значениях априорных вероятностей состояний природы возможен и другой выбор. Используя данные табл.3 и формулу (6) для каждой операции а_i, i = 1,2,3, имеем

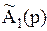= р +11(1 – p) = 11 – 10p,

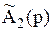= 10p +6(1 – p) = 6 + 4p,

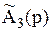= 14(1 – p) = 14 – 14p.

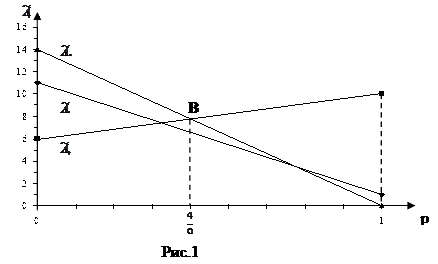На рис.1 даны графики функций 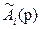, i = 1, 2,

Прямые 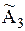, 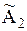пересекаются в точке В, при 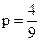, вычисленного из равенства 6 + 4р = 14 – 14р. Из рис. 1 следует, что при 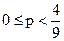лучшей операцией является а₃, а при 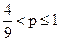лучшей операцией является а₂. При 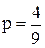безразлично, какую операцию а₂ или а₃ использовать. Операцию а₁ применять невыгодно.

Если р=0 или 1, то имеем ситуацию ПР в условиях достоверности. При р=0 лучшая операция – а₃, при р=1 лучшая операция – а₂.

Дата добавления: 2014-01-15