Принятие решений в условиях неопределенности

Принятие решений при проведении эксперимента.

Допустим, что вероятности р(Q₁), р(Q₂), …, р(Q_n) в принципе существуют, но вам неизвестны. Иногда в этом случае предполагают все состояния природы равновероятными (так называемый «принцип недостаточного основания» Лапласа), но вообще-то это делать не рекомендуется. Все-таки обычно более или менее ясно, какие состояния более, а какие - менее вероятны. Для того чтобы найти ориентировочные значения вероятностей р(Q₁), р(Q₂), …, р(Q_n), можно, например, воспользоваться методом экспертных оценок. Хоть какие-то ориентировочные значения вероятностей состояния природы все же лучше, чем полная неизвестность. Неточные значения вероятностей состояний природы в дальнейшем могут быть «скорректированы» с помощью специально поставленного эксперимента. Эксперимент может быть как «идеальным», полностью выясняющим состояние природы, так и неидеальным, где, вероятности состояний уточняются по косвенным данным

Человек, прежде чем принять решение, пытается получить некоторую информацию о состоянии природы экспериментальным путем. Предполагается, что проведение эксперимента не требует никаких затрат,

Пусть проведен эксперимент, имеющий t исходов – возможных прогнозов состояния природы,

Z=(z₁, z₂,…, z_t), .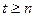

Известна условная вероятность Р(z_β/Q_j) b-го результата эксперимента при состоянии природы Q_j,

P_bj= Р(z_β/Q_j), b=1,2,…,t, j=1,2,…,n. (7)

Множество значений P_bj можно представить в виде матрицы размера t·n, данной в табл. 5.

Для использования информации, полученной в результате эксперимента, введем понятие стратегии.

Таблица 5

Qj Zb	Q1	Q2	…	Qn
z1	P11	P12	…	P1n
z2	P21	P22	…	P2n
…	…	…	…	…
zt	Pt1	Pt2	…	Ptn

Стратегия - это соответствие последовательности t результатов эксперимента последовательности t операций,

(z₁, z₂,…, z_t)→ (a_i, a_j,…, a_k). (8)

Выражение (8) подразумевает, что

z₁→ a_i, ,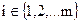

z₂→ a_j, ,

……………………

z_t→ a_k, .

Число возможных стратегий l определяется формулой

l = m^t,

m – число операций, t - число результатов эксперимента. При m=2, t=3 всевозможные стратегии представлены в табл.6.

Таблица 6

Si zb	S1	S2	S3	S4	S5	S6	S7	S8
z1	a1	a1	a1	a1	а2	а2	а2	а2
z2	a1	a1	а2	а2	a1	a1	а2	а2
z3	a1	а2	a1	а2	a1	а2	a1	а2

Задача ПР формулируется так: какую одну из операций a₁,a₂,…, a_m следует выбрать в зависимости от одного из результатов эксперимента z₁, z₂,…, z_t.

Для принятия решения находим усредненные полезности стратегий S_i, i= 1,2, …, l, при состояниях природы Q_j, j=1, 2, …, n,

U(S_i,Q_j)=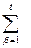α_{i β j} P_{β j}, i= 1,2, …, l, j=1, 2, …, n, (9)

где α_iβj - полезность β-ой компоненты i-ой стратегии при состоянии природы Q_j, P_βj – условная вероятность β-го результата эксперимента при состоянии природы Q_j. Стратегия S_i определена множеством операций, значения α_{i β j} берутся из таблицы полезностей значения P_βj – из табл. 5. Полученные значения усредненных полезностей U(S_i,Q_j) можно записать в виде матрицы размера n·l. Для принятия решения – выбора наилучшей стратегии можно воспользоваться уже рассмотренными критериями: максимина, минимакса сожалений и равновозможных состояний.

Рассмотрим конкретный пример. Предполагается лишь два состояния природы: Q₁ - теплая погода, Q₂ – холодная погода, и только две операции: a₁ – одеться для теплой погоды, a₂ – одеться для холодной погоды. Эта ситуация характерна для туристов. Матрица полезности дана в табл.7.

Таблица 7 Таблица 8

Qj ai

Q1

Q2

Qj zb

Q1

Q2

a1

z1

0.6

0.3

z2

0.2

0.5

a2

z3

0.2

0.2

Критерий максимина гарантирует 4 ед. полезности и рекомендует выбирать операцию а₂. Критерий минимакса дает этот же ответ.

Но есть возможность воспользоваться данными прогноза погоды (в этом и состоит эксперимент), которые могут быть трех видов:

z₁ – ожидается теплая погода,

z₂ – ожидается холодная погода,

z₃ – прогноз неизвестен.

Из прошлого опыта известны условные вероятности этих трех видов прогноза для каждого состояния природы , b=1,2,3, j =1,2, представленные в табл. 8.

Для каждой из 8–ми стратегий и каждого из 2–х состояний природы определим взвешенные суммы полезностей по формуле (9), используя данные таблиц 6 – 8,

U(S₁,Q₁) =10×0.6 + 10×0.2 +10×0.2 =10,

U(S₂,Q₁) =10×0.6 + 10×0.2 +4×0.2 = 8.8,

U(S₃,Q₁) =10×0.6 + 4×0.2 + 10×0.2 = 8.8,

........................................................

U(S₈,Q₁) = 4×0.6 + 4×0.2 + 4×0.2 = 4,

U(S₁,Q₂) = 0×0.3 + 0×0.5 +0×0.2 = 0,

.........................................................

U(S₈,Q₂) = 7×0.3 + 7×0.5 + 7×0.2 = 7.

Все вычисленные значения U(S_i,Q_j), i = 1,2,…8, j = 1, 2, помещены в табл.9.

Таблица 9

Si Qj	S1	_ S2	S3	S4	_ S5	_ S6	S7	S8
Q1		8.8	8.8	7.6	6.4	5.2	5.2
Q2		1.4		4.9	2.1		5.6

Из табл. 9 предварительно следует исключить плохие стратегии –– те стратегии, обе компоненты которых не больше (£) соответствующих компонент какой–либо другой стратегии. Ввиду того, что , , 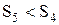S₆ ≤ S₇, то стратегии 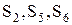исключаются из рассмотрения (в табл. 9 они помечены знаком "–").

К оставшимся, допустимым стратегиям можно применить известные нам критерии. Используя критерий максимина, имеем:

, ,

, , ,

.

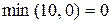Следовательно, наилучшей стратегией является стратегия S₇, гарантирующая 5.2 ед. полезности. Для сравнения максиминная операция гарантирует лишь 4 ед. полезности. Так как S₇ = (a₂, a₂, a₁), то в силу (8) имеем

.

Это значит, что при прогнозе z₁ выбирается операция а₂, при прогнозе z₂ – a₂, при прогнозе z₃ – a₁, т.е. максиминная стратегия S₇ рекомендует одеваться тепло, если прогноз – теплая или холодная погода, и одеваться легко, если прогноз неизвестен. Последнее утверждение весьма непрактично.

Максиминная стратегия S₇ при неблагоприятном стечении обстоятельств может привести и к худшему результату, чем максиминная операция . Например, имеет место холодная погода 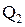. Тогда согласно максиминной операции турист получит 7 ед. полезности (табл. 7). С другой стороны, если результат прогноза будет (прогноз неизвестен) и согласно стратегии S₇ будет выбрана операция (одеться легко), то он получит 0 ед. полезности. Это явление –– типичное для теории игр и теории принятия решений. S₇ гарантирует лишь среднюю полезность в 5.2 ед.

3.2. Использование смешанной стратегии

Стратегия S^* называется смешанной, если она представлена в виде выпуклой комбинации двух других стратегий,

S^* = сS_m1 + (1 - с)S_m2, 0<с<1, m₁, m₂ Î {1, 2, …, t}.

Это определение базируется на понятии выпуклой комбинации точек [14]. Переход к смешанной стратегии осуществляется с целью повышения гарантированной средней полезности.

Стратегии рассмотренного выше примера изобразим точками на плоскости с координатами , , i=1,3,4,7,8 (рис. 2).

По рис. 2 видно, что если взять в определенных пропорциях стратегии S₄ и S₈, то получим смешанную стратегию, лучшую по сравнению со стратегией S₇. Проведем биссектрису I-го координатного угла и найдем точку пересечения ее с отрезком [S₄, S₈] –– точку .

Запишем уравнение прямой, проходящей через точки S₄(7.6; 4.9), S₈ (4;7),

,

которое приводится к виду:

.

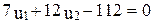Из этого уравнения находим координаты точки , для которой ,

.

Так как 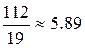, то стратегия лучше стратегии S₇, гарантирующей 5.2 ед. полезности, S^*>S₇. Теперь остается представить стратегию в виде выпуклой комбинации стратегий S₄, S₈,

S^* = cS₄ + (1 – c)S₈, 0 < c <1. (10)

Для определения значения параметра a достаточно записать уравнение (10) для абсцисс входящих в него точек,

из которого получаем 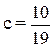. Тогда равенство (10) принимает вид:

. (11)

Так как , , то в силу равенства (11) имеем

.

Практически смешанную стратегию S^* можно реализовать так. Если результат эксперимента есть z₂ или z₃, то используется операция a₂. Если же результат эксперимента есть z₁, то с помощью подходящего случайного механизма с вероятностью 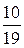используется операция a₁, и с вероятностью 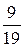–– операция а₂. Основой случайного механизма могут служить 19 одинаковых карточек, на 10–и из которых записан символ а₁, а на 9–и –– символ а₂. Из этого набора 19–и карточек случайно выбирается одна и используется та операция, символ, которой изображен на этой карточке.

3.3. Принятие решений в условиях риска

К условиям, перечисленным в подпараграфе 3.1, добавляется еще одно – значения априорных вероятностей состояний окружающей среды (природы):

p(Q₁), p(Q₂),..., p(Q_n). (12)

Тогда для каждой стратегии определяется усредненная по всем состояниям природы средняя полезность по формуле:

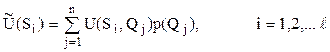(13)

U(S_i,Q_j) – полезность стратегии 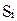при состоянии природы 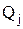, которая находится по формуле (9). Затем из множества , , выделяется максимальный элемент,

, .Стратегия , обладающая максимальной средней полезностью , называется байесовской стратегией,

, .

Пусть в рассмотренном ранее примере р(Q₁) = 0.6, p(Q₂) = 0.4. Используя данные табл. 9. и формулу (13), вычислим среднюю полезность для каждой допустимой стратегии,

= 10×0.6 + 0×0.4 = 6,

= 8.8×0.6 + 5×0.4 = 6.68,

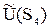= 7.6×0.6 + 4.9×0.4 = 6.52,

= 5.2×0.6 +5.6×0.4 =5.36,

= 4×0.6 + 7×0.4 =5.2.

Затем найдем наибольшее число из полученных пяти чисел,

Следовательно, оптимальной стратегией является стратегия , обладающая максимальной средней полезностью, равной 6.68 ед.

Заметим, что стратегия является байесовской для конкретных значений априорных вероятностей: р(Q₁) = 0.6, p(Q₂) = 0.4. При других значениях р(Q₁), р(Q₂) байесовской может быть и другая стратегия. Так, при р(Q₁) = 0.5, p(Q₂) = 0.5 байесовской является стратегия .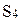

Проведение эксперимента в рассмотренной ситуации выгодно. Действительно, если эксперимент не проводить, то по данным табл.7 имеем:

Байесовской операцией (стратегией) является операция а₁, средняя полезность которой равна 6 ед.

Для дальнейших рассуждений нам понадобиться объединить выражения (13), (9) в одно,

.

Меняя порядок суммирования в правой части последнего равенства, получим

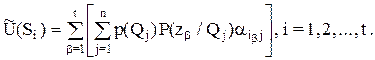(14)

Из этого равенства следует, что при выборе оптимальной стратегии 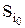максимизация сводится к максимизации выражения в квадратных скобках в правой части (14), т.е. для каждого результата эксперимента z_β максимизация полезности U_β(a_i) сводится к выбору такой операции 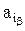, которая максимизирует выражение в квадратных скобках.

ЛИТЕРАТУРА.

1. Венцель Е.С. Исследование операций. Задачи, принципы, методология. - М: Наука, 1980.

2. Дегтярев Ю.П. Исследование операций. - М.: Высшая школа, 1986.

3. Корбут А.А., Финкелыптейн Ю.Ю. Дискретное программирование. -М.:Мир, 1978.

4. Кристофвдес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978.

5. Липский В. Комбинаторика для программистов. - М.: Мир, 1988.

6. Клейнрок Л. Теория массового обслуживания. - М.: Машиностроение, 1979.

7. Ивченко Г.И. и др. Теория массового обслуживания. - М. Высшая школа, 1982.

8. Шенок Р. Имитационное моделирование систем - искусство и наука.-М.: Мир, 1978.

9. Гудман С, Хидегниеми С. Введение в разработку и анализ алгоритмов. - М.: Мир, 1981.

10. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва «Высшая школа» 1998.

Дата добавления: 2014-01-15