
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 2. Графическое изображение рядов распределения
|
|
|
|
Первым этапом анализа рядов распределения является их графическое изображение. В этом случае строят специальные графические объекты: полигон распределения частот, гистограмму, кумуляту и огиву распределения.
1. Полигонраспределения частот обычно используется для изображения дискретных вариационных рядов. Он строится в прямоугольной системе координат. На оси абсцисс через равные интервалы (часто через единичный отрезок) отображаются ранжированные значения варьирующего признака. На оси ординат наносится шкала для выражения численности каждой варианты, т.е. частоты вариант. В результате, соединив прямыми линиями точки, соответствующие данным, отложенным по оси абсцисс и ординат, получают ломаную линию, называемую полигоном распределения частот.
Пример построения полигона распределения компаний по размеру годового дохода приведен на рисунке 3.1. В качестве исходной информации выступают данные таблицы 3.3.
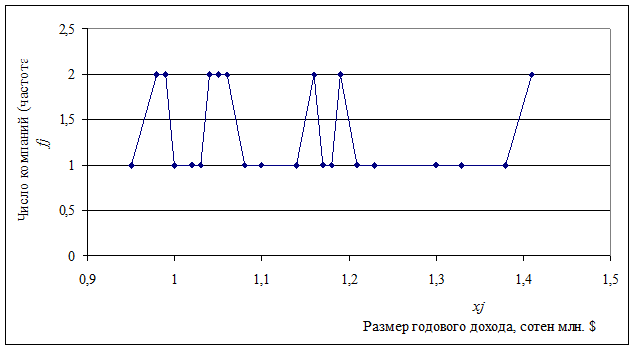
Рис. 3.1. Полигон распределения 30 компаний мира по размеру годового дохода
2. Гистограмма распределения частот применяется для изображения интервальных вариационных рядов. Отображение величин интервалов осуществляется на оси абсцисс, а частоты описываются прямоугольниками, построенными на данных интервалах вдоль оси ординат. Высота каждого прямоугольника равна частоте соответствующего интервала, а ширина столбика – ширине интервала.
Пример построения гистограммы на основе равноинтервальной группировки (табл. 3.4) приведен на рисунке 3.2.

Рис. 3.2. Гистограмма равноинтервального распределения 30 компаний мира
по размеру годового дохода
Гистограмма интервального ряда распределения может быть совмещена с полигоном. Для этого следует отметить точками середины верхних сторон прямоугольников гистограммы и соединить точки прямыми линиями (рис. 3.3).
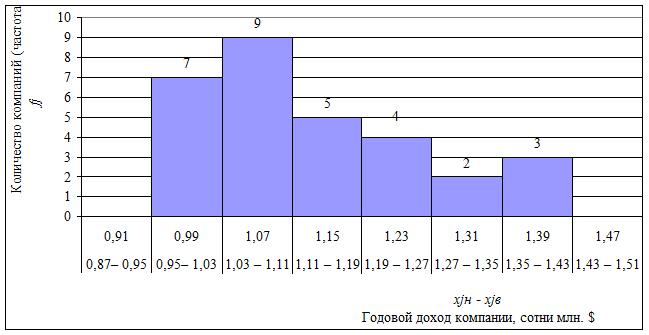
Рис. 3.3. Гистограмма и замкнутый полигон равноинтервального распределения
30 компаний мира по размеру годового дохода
На рисунке 3.3 полигон распределения частот замкнут: справа и слева от гистограммы отложено по одному интервалу (ширина 0,08 сотен млн. $), середины отложенных интервалов отмечены точками и соединены со всеми остальными точками полигона. Замыкание полигона на ось абсцисс обеспечивает равенство площадей гистограммы и области, отсекаемой полигоном.
3. Для графического изображения дискретных и интервальных вариационных рядов также может использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот или частостей. Накопленные частоты (частости) вычисляются суммированием частот (частостей) по изучаемым группам и показывают количество единиц совокупности, имеющих значения признака не больше, чем указанное.
При построении кумуляты интервального вариационного ряда на оси абсцисс отмечают варианты ряда, на оси ординат – накопленные частоты (частости). Эти точки соединяют прямыми и получают кумуляту.
Пример. Построение кумуляты следует предварить расчетом накопленных частот и частостей. Для этого добавим к таблице 3.4 дополнительные столбцы – 6, 7 и 8 – и построим таблицу 3.4¢.
Таблица 3.4¢.
Равноинтервальный ряд распределения 30 компаний мира
по размеру годового дохода
| № гр. | Группы компаний по размеру годового дохода (100 млн. $) | Ширина интервала группировки (100 млн. $) | Число компаний в группе | Накоп-ленные частоты | Накоп-ленные частости, % | Значение признака, стоящее в середине интервала (100 млн. $) | |
| абсолютное (частота) | относи-тельное – в % к итогу (частость) | ||||||
| j | 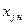 – – 
| 
| fj | dj | 
| 
| 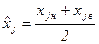
|
| 0,95– 1,03 | 0,08 | 23,3 | 23,3 | 0,99 | |||
| 1,03 – 1,11 | 0,08 | 53,3 | 1,07 | ||||
| 1,11 – 1,19 | 0,08 | 16,7 | 1,15 | ||||
| 1,19 – 1,27 | 0,08 | 13,3 | 83,3 | 1,23 | |||
| 1,27 – 1,35 | 0,08 | 6,7 | 1,31 | ||||
| 1,35 – 1,43 | 0,08 | 1,39 | |||||
| ВСЕГО | – | 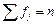 = 30 = 30
| – | – |
Накопленная частота первого интервала равна его обычной частоте:  7 компаний. Накопленная частота второго интервала содержит сумму частот первого и второго интервала:
7 компаний. Накопленная частота второго интервала содержит сумму частот первого и второго интервала: 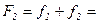 7 + 9 = 16 компаний. Накопленная частота третьего интервала:
7 + 9 = 16 компаний. Накопленная частота третьего интервала:  7 + 9 + 5 =21 компания и т.д. Накопленная частота последнего, шестого, интервала равна общему числу единиц наблюдения:
7 + 9 + 5 =21 компания и т.д. Накопленная частота последнего, шестого, интервала равна общему числу единиц наблюдения:  30 компаний.
30 компаний.
Аналогично рассчитываются и накопленные частости. Накопленная частость последнего интервала равна сумме всех частостей: 
=23,3 + 30 + 16,7 + 13,3 + 6,7 +10 = 100%.
Изобразим кумуляту распределения компаний по размеру годового дохода, выбрав в качестве значений оси ординат накопленные частоты. Координатой, откладываемой по оси абсцисс, изберем значение признака, соответствующее середине каждого интервала. Его расчетное значение получим по формуле (3.2):
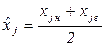 , (3.2)
, (3.2)
где 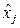 – значение признака в середине j -го интервала (не то же, что среднее значение признака в интервале!), сотни млн. $;
– значение признака в середине j -го интервала (не то же, что среднее значение признака в интервале!), сотни млн. $;
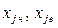 – нижняя и верхняя граница интервала, сотни млн. $.
– нижняя и верхняя граница интервала, сотни млн. $.
Значения признака, стоящие в середине каждого интервала, рассчитаны в столбце 8 таблицы 3.4¢. Полученная кумулята изображена на рисунке 3.4.
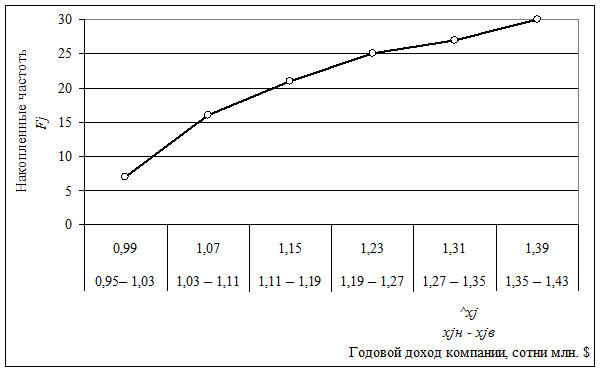
Рис. 3.4. Кумулята равноинтервального распределения 30 компаний мира
по размеру годового дохода (по накопленным частотам)
4. Если оси абсцисс и ординат кумуляты поменять местами, то получается огива.
Наибольшее практическое значение для анализа интервальных рядов распределения имеет гистограмма. По симметричности убывания высот ее столбиков от самого высокого (пикового) выносят предварительное суждение о близости фактического распределения частот нормальному закону распределения. Так, из данных рисунка 3.3 видно, что фактическое распределение компаний по интервалам размера годового дохода (7, 9, 5, 4, 2 и 3 компании) отличается от нормального. В нормальном распределении частоты плавно возрастают, в центральном интервале имеют пик значений, а затем также плавно и симметрично снижаются.
Тема 4. Обобщающие статистические показатели
1. Абсолютные показатели: сущность и единицы измерения
2. Относительные показатели: сущность и значения, формы выражения и виды
Статистический показатель – количественная характеристика изучаемого объекта или его свойства.
Обобщающие статистические показатели – показатели, характеризующие совокупность единиц, объединенных в группы или в целом.
В зависимости от метода расчета обобщающие статистические показатели могут быть:
- абсолютными;
- относительными;
- средними.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 3408; Нарушение авторских прав?; Мы поможем в написании вашей работы!