
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 1. Понятие и виды рядов распределения
|
|
|
|
Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному признаку.
В зависимости от признака, положенного в основу ряда распределения, различают атрибутивные и вариационные ряды распределения.
I. Атрибутивными называют ряды распределения, построенные по качественным признакам.
Пример. Группировка населения РФ по уровню образования (табл. 3.1).
Таблица 3.1.
Атрибутивный ряд распределения населения РФ по уровню образования в 2006 г.*
| Категория населения по уровню образования | Все население в возрасте 15 лет и более, млн. чел. | В % к итогу | ||
| Имеющие образование | профессиональное | послевузовское | 369,1 | 0,3 |
| высшее | 19 009,3 | 15,6 | ||
| неполное высшее | 3 739,7 | 3,1 | ||
| среднее | 32 929,2 | 27,1 | ||
| начальное | 15 366,9 | 12,7 | ||
| Общее | среднее (полное) | 21 276,6 | 17,5 | |
| основное | 16 695,3 | 13,7 | ||
| начальное | 9 349,8 | 7,6 | ||
| Не имеющие начального общего образования | 1 200,0 | 0,8 | ||
| из них неграмотные | 670,5 | 0,5 | ||
| Не указавшие уровень образования | 1 364,4 | 1,1 | ||
| Всего | 121 300,2 | |||
| * Источник: Данные Переписи населения 2002 г. Режим доступа: http://www.perepis2002.ru/ct/doc/TOM_03_01.xls |
II. Вариационными называют ряды распределения, построенные по количественному признаку.
В зависимости от характера вариации выделяется два вида вариационных рядов распределения: дискретные и интервальные. Перед их построением массив исходных данных следует ранжировать.
Массив ранжированных данных (МРД) – это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака. Таким образом, в МРД выделяется только один элемент – варианты признака xi.
Вариантами массива ранжированных данных (xi)называются индивидуальные значения признака.
Пример. В таблице 3.2 представлен массив ранжированных данных 30 компаний, входящих в рейтинг крупнейших компаний мира Global-500, по размеру совокупного дохода в истекшем финансовом году.
Обозначим через i номер индивидуальных вариант в массиве ранжированных данных, тогда i=1, 2, …, п в общем случае и i=1, 2, …, 30 в нашем примере. Тогда изучаемый признак х – годовой доход компании – можно обозначить как xi. Например, совокупный доход четвертой по рангу компании (ОАО «Газпром») составил в истекшем году 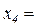 99 млн. $.
99 млн. $.
Таблица 3.2.
Массив ранжированных данных (30 компаний мира)
по увеличению размера годового дохода
| Место (ранг) i | Company Наименование компании | Revenues (100 millions $) Годовой доход компании (100 млн. $) xi |
| Nissan Motor | 0,95 | |
| Valero Energy | 0,98 | |
| Hitachi | 0,98 | |
| Gazprom | 0,99 | |
| International Business Machines | 0,99 | |
| HBOS | 1,00 | |
| McKesson | 1,02 | |
| Societe Generale | 1,03 | |
| Pemex | 1,04 | |
| Hewlett-Packard | 1,04 | |
| Honda Motor | 1,05 | |
| ArcelorMittal | 1,05 | |
| Samsung Electronics | 1,06 | |
| Siemens | 1,06 | |
| Royal Bank of Scotland | 1,08 | |
| American International Group | 1,10 | |
| Assicurazioni Generali | 1,14 | |
| Carrefour | 1,16 | |
| J.P. Morgan Chase & Co. | 1,16 | |
| UBS | 1,17 | |
| Berkshire Hathaway | 1,18 | |
| AT&T | 1,19 | |
| Bank of America Corp. | 1,19 | |
| ENI | 1,21 | |
| Deutsche Bank | 1,23 | |
| China National Petroleum | 1,30 | |
| State Grid | 1,33 | |
| Crйdit Agricole | 1,38 | |
| Allianz | 1,41 | |
| BNP Paribas | 1,41 | |
| Источник: Электронная версия журнала CNN Режим доступа: http://money.cnn.com/magazines/fortune/global500/2008/full_list/401_500.html |
В дискретном и интервальном рядах распределения обязательными являются два элемента – варианты и частоты признака.
Вариантами дискретного или интервального рядов распределения(xj)называются групповые значения признака в ряду.
Частоты (fj) – это численности каждой группы вариант (xj) вариационного ряда, т.е. это числа, показывающие, как часто встречаются (или как часто повторяются) те или иные группы вариант в дискретном или интервальном ряду распределения.
Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями (dj):
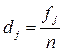 или
или 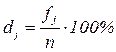 . (3.1)
. (3.1)

| Важно! До момента построения массива ранжированных данных исходная информация называется массивом несгруппированных данных. И массив несгруппированных данных, и массив ранжированных данных представлены совокупностью единиц, обладающих индивидуальными значениями изучаемого признака х. В связи с этим в обозначении вариант признака имеется нижний индекс – i: 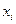 . Например, . Например, 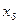 - значение признака восьмой единицы совокупности в массивах исходных (несгруппированных) и ранжированных данных.
Дискретными и интервальными рядами распределения признаются ряды, состоящие из двух элементов: групповых (j -тых) значений признака хj и соответствующих им частот fj, где j – номер группы.
Каждая i -я единица исходной совокупности при группировке попадает в j -ю группу, поэтому в обозначении индивидуальных сгруппированных вариант признака появляются два нижних индекса – i и j: - значение признака восьмой единицы совокупности в массивах исходных (несгруппированных) и ранжированных данных.
Дискретными и интервальными рядами распределения признаются ряды, состоящие из двух элементов: групповых (j -тых) значений признака хj и соответствующих им частот fj, где j – номер группы.
Каждая i -я единица исходной совокупности при группировке попадает в j -ю группу, поэтому в обозначении индивидуальных сгруппированных вариант признака появляются два нижних индекса – i и j: 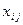 . Например, . Например, 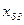 - значение признака восьмой единицы совокупности, попавшей в третью группу. - значение признака восьмой единицы совокупности, попавшей в третью группу.
|
1.Дискретный вариационный ряд (ДВР) характеризует распределение единиц совокупности по дискретному признаку. В случае дискретной вариации в качестве значения признака выступает число (величина абсолютная или относительная, целая или дробная, положительная или отрицательная), а не интервал значений признака от… и до….
Построение дискретного вариационного ряда осуществляется с помощью метода группировок. Номера групп помечают символом j, тогда в общем случае j=1, 2, …, 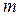 . Варианты признака х в этом случае принимают обозначение хj. Число групп
. Варианты признака х в этом случае принимают обозначение хj. Число групп 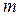 для дискретного признака при небольшом количестве различных значений будет равно этому количеству, при большом количестве различных значений дискретного признака строится интервальный вариационный ряд.
для дискретного признака при небольшом количестве различных значений будет равно этому количеству, при большом количестве различных значений дискретного признака строится интервальный вариационный ряд.
Пример. В таблице 3.2 встречается 22 различных значения годового дохода 30 компаний мира: 0,95; 0,98; 0,99; … 1,41 сотен млн. $. Каждое из них составит отдельную группу дискретного вариационного ряда, представленного в таблице 3.3 (варианты признака xj расположены в столбце 2).
Таблица 3.3.
Дискретный ряд распределения крупнейших компаний мира
по размеру годового дохода
| Номер группы | Группы компаний по размеру годового дохода (сотни млн. $) | Число компаний в группе | |
| абсолютное (частота) | относительное – в % к итогу (частость) | ||
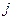
| xj | fj | dj |
| 0,95 | 3,3 | ||
| 0,98 | 6,7 | ||
| 0,99 | 6,7 | ||
| 1,00 | 3,3 | ||
| 1,02 | 3,3 | ||
| 1,03 | 3,3 | ||
| 1,04 | 6,7 | ||
| 1,05 | 6,7 | ||
| 1,06 | 6,7 | ||
| 1,08 | 3,3 | ||
| 1,10 | 3,3 | ||
| 1,14 | 3,3 | ||
| 1,16 | 6,7 | ||
| 1,17 | 3,3 | ||
| 1,18 | 3,3 | ||
| 1,19 | 6,7 | ||
| 1,21 | 3,3 | ||
| 1,23 | 3,3 | ||
| 1,30 | 3,3 | ||
| 1,33 | 3,3 | ||
| 1,38 | 3,3 | ||
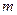 =22 =22
| 1,41 | 6,7 | |
| ВСЕГО | 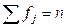 = 30 = 30
|
Столбец 3 таблицы 3.3 заполняется путем непосредственного подсчета числа компаний, имеющих то или иное значение годового дохода. Так, по столбцу 3 таблицы 3.2 видно, что размером годового дохода в 0,95 сотен млн. $ обладает одна компания: в графе 3 таблицы 3.3 появляется запись 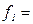 1. Для 0,98 и 0,99 сотен млн. $ (группы 2 и 3) частоты равны двум:
1. Для 0,98 и 0,99 сотен млн. $ (группы 2 и 3) частоты равны двум: 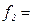 2 и
2 и 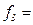 2 компании. Частота четвертой группы (с размером годового дохода 1,00 сотен млн. $) составляет
2 компании. Частота четвертой группы (с размером годового дохода 1,00 сотен млн. $) составляет 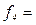 1 компанияи т.д. Сумма всех частот равна числу единиц наблюдения (
1 компанияи т.д. Сумма всех частот равна числу единиц наблюдения (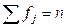 = 30 компаний, итог столбца 3 таблицы 3.3).
= 30 компаний, итог столбца 3 таблицы 3.3).
Столбец 4 таблицы 3.3 заполняется путем расчета частостей по формуле (3.1). Так, частость первой группы равна 3,3%:
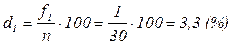 .
.
Аналогично определяем:
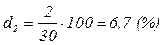 ;
;
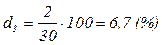 . Это означает, что 6,7% компаний (2 из 30) в истекшем году обладали размером годового дохода 0,99 сотен млн. $. В их число вошел и концерн «Газпром»;
. Это означает, что 6,7% компаний (2 из 30) в истекшем году обладали размером годового дохода 0,99 сотен млн. $. В их число вошел и концерн «Газпром»;
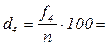
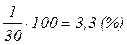 и т.д.
и т.д.
Как видно из таблицы 3.3, дискретный вариационный ряд имеет большое число групп – 22 группы для 30 единиц наблюдения (компаний). Кроме того, в 14 группах из 22 частота fj не превышает единицы. Это говорит о большой вариации признака – размера годового дохода – в пределах совокупности 30 компаний, что затрудняет анализ полученных данных. Для устранения данного недостатка построим интервальный вариационный ряд компаний с помощью метода группировок.
3.Интервальный вариационный ряд (ИВР) строится при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких пределах. В этом случае в качестве вариант значений признака выступает
интервал значений с границами от… и до…
В отличие от обычной группировки данных, в интервальных вариационных рядах распределения принципиальным является вопрос о количестве единиц наблюдения в каждой группе, т.е. изучается характер распределения частот по выделенным группам значений признака. Чтобы выявить характер распределения, число групп принимается оптимальным (по формуле Стерджеса), проводится построение ряда методом группировки данных, а затем фактические частоты сравниваются с теоретическими частотами, отвечающими нормальному закону распределения случайных величин. В случае резкого отличия фактических частот от теоретических число интервалов корректируется в сторону увеличения или уменьшения до тех пор, пока фактическое распределение частот не приблизится к нормальному (теоретическому).
Пример. Построим равноинтервальный вариационный ряд 30 компаний мира по размеру годового дохода.
Количество групп определим по таблице 2.1. Поскольку число единиц наблюдения n=30 компаний, то оптимальное число групп составляет 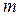 =6 групп.
=6 групп.
Ширину интервала рассчитаем по формуле (2.1):
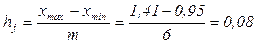 сотен млн. $.,
сотен млн. $.,
где 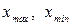 – максимальное и минимальное значение признака в совокупности;
– максимальное и минимальное значение признака в совокупности;
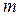 – число групп.
– число групп.
Нижней границей первого интервала принимаем минимальное значение дохода в совокупности компаний – 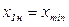 = 0,95 сотен млн. $. Прибавляем к ней ширину интервала группировки –
= 0,95 сотен млн. $. Прибавляем к ней ширину интервала группировки – 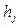 = 0,08 сотен млн. $. – и получаем верхнюю границу первого интервала группировки:
= 0,08 сотен млн. $. – и получаем верхнюю границу первого интервала группировки: 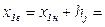 0,95+0,08 = 1,03 сотен млн. $. Полученные значения записываем в первую строку столбца 2 таблицы 3.4.
0,95+0,08 = 1,03 сотен млн. $. Полученные значения записываем в первую строку столбца 2 таблицы 3.4.
Нижней границей второго интервала принимаем верхнюю границу первого интервала: 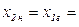 1,03 сотен млн. $. Для получения верхней границы второго интервала вновь к нижней границе прибавляем ширину интервала группировки:
1,03 сотен млн. $. Для получения верхней границы второго интервала вновь к нижней границе прибавляем ширину интервала группировки: 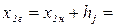 1,03 + 0,08 = 1,11 сотен млн. $. Результат записываем во вторую строку столбца 2 таблицы 3.4.
1,03 + 0,08 = 1,11 сотен млн. $. Результат записываем во вторую строку столбца 2 таблицы 3.4.
и т.д.
Таблица 3.4.
Равноинтервальный ряд распределения 30 крупнейших компаний мира
по размеру годового дохода
| Номер группы | Группы компаний по размеру годового дохода (100 млн. $) | Ширина интервала группировки (100 млн. $) | Число компаний в группе | |
| абсолютное (частота) | относительное – в % к итогу (частость) | |||
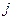
| 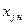 – – 
| 
| fj | dj |
| 0,95– 1,03 | 0,08 | 23,3 | ||
| 1,03 – 1,11 | 0,08 | |||
| 1,11 – 1,19 | 0,08 | 16,7 | ||
| 1,19 – 1,27 | 0,08 | 13,3 | ||
| 1,27 – 1,35 | 0,08 | 6,7 | ||
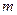 =6 =6
| 1,35 – 1,43 | 0,08 | ||
| ВСЕГО | – | 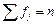 = 30 = 30
|
Столбец 3 таблицы 3.4 подтверждает, что построена равноинтервальная группировка: ширина каждого интервала одинакова и составляет 0,08 сотен млн. $.
Столбец 4 таблицы 3.4 заполняем путем подсчета числа компаний, обладающих тем или иным значением годового дохода. Подсчет можно вести как по массиву ранжированных данных (табл. 3.2, столбец 3), так и по дискретному вариационному ряду (табл. 3.3, столбец 3). Например, в первую группу с годовым доходом от 0,95 до 1,03 сотен млн. $ вошло 7 компаний[1], во вторую группу с доходом от 1,03 до 1,11 сотен млн. $ – 9 компаний и т.д. Сумма всех частот равна числу единиц наблюдения (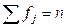 = 30 компаний, итог столбца 4 таблицы 3.4).
= 30 компаний, итог столбца 4 таблицы 3.4).
Частоты всех интервалов отличны от нуля, поэтому повторную группировку проводить не следует.
Вывод: согласно данным интервального вариационного ряда, наибольшее число компаний – 9 из 30 (или 30%) – имеют годовой доход от 1,03 до 1,11 сотен млн. $.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2393; Нарушение авторских прав?; Мы поможем в написании вашей работы!