Средняя арифметическая

1.1. Средняя арифметическая простая – используется в том случае, когда расчет ведется по массиву несгруппированных или ранжированных данных. Получается при подстановке в формулу (5.1) среднестепенной простой коэффициента k=1.

, (5.3)

где 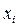– индивидуальные варианты значений признака;

п – число вариант.

Пример. Воспользуемся данными таблицы 3.2 для расчета среднего значения годового дохода 30 крупнейших компаний мира в истекшем году:

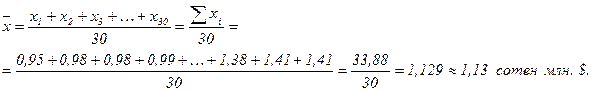
1.2. Средняя арифметическая взвешенная – используется в том случае, когда расчет ведется по дискретному или интервальному ряду распределения.

а). Средняя арифметическая взвешенная в дискретном ряду распределения получается при подстановке в формулу среднестепенной взвешенной (5.2) коэффициента k=1:

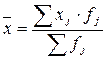, (5.4)

где j – номер группы (j=1, 2, …, т);

х_j – отдельные значения варьирующего признака (варианты);

f_j – частоты j -ой группы.

Если в качестве весов выступают не частоты, а частости, то формула средней арифметической взвешенной имеет один из двух видов:

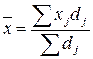
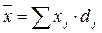
		(5.5)
частости 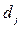выраженны в процентах	частости 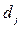выражены в долях единицы (коэффициентах)

Пример. Воспользуемся данными таблицы 3.3 для расчета среднего значения годового дохода 30 компаний мира:

- по формуле (5.4):

- по формуле (5.5), частости выражены в процентах:

б).Средняя арифметическая взвешенная в интервальном ряду распределения такжерассчитывается по формулам (5.4), (5.5), однако в качестве вариант признака выбираются середины интервалов группировки. Полученная средняя величина носит название средней арифметической взвешенной через середины интервалов. Для ее расчета применение формул (5.4), (5.5) разбивается на 2 шага:

1 шаг. Находится середина интервала (), т.е. полусумма верхней и нижней границы каждого внутреннего интервала:

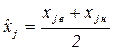. (5.6)

2 шаг. Найденные середины интервалов () принимаются в качестве значений признака при расчете общей средней и подставляются в произведение числителя дробей (5.4) и (5.5):

. (5.7)

		(5.8)
частости 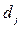выражены в процентах	частости 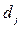выражены в долях единицы (коэффициентах)

Пример. В столбце 6 таблицы 3.4′ середины интервалов уже были рассчитаны. Теперь осталось рассчитать среднее значение стоимости годового дохода 30 компаний:

- по формуле (5.7):

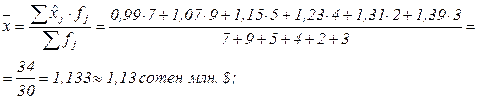
-по формуле (5.8), частости выражены в процентах:

Вывод: среднее значение годового дохода 30 компаний мира в истекшем году составило по данным дискретного вариационного ряда около 1,13 (точно 1,129) сотен млн. $, по данным интервального вариационного ряда – около 1,13 (точно 1,133) сотен млн. $.

2. Средняя гармоническая – вычисляется, когда нужно суммировать не сами варианты, а обратные им величины. Получается при подстановке в формулы среднестепенной простой (5.1) и среднестепенной взвешенной (5.2) коэффициента k=-1.

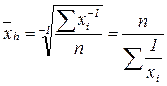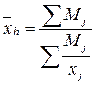, . (5.10)

К средней гармонической взвешенной следует прибегать в тех случаях, когда в качестве весов используются не единицы совокупности, носительницы признака, а произведения этих единиц на значения признака (М_j=x_j × f_j):

3. Средняя геометрическая – используется для анализа динамики явлений и позволяет определить средний коэффициент роста. Получается при подстановке в формулы среднестепенной простой (5.1) и взвешенной (5.2) коэффициента k=0.

. (5.11)

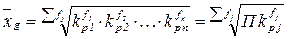. (5.12)

При расчете средней геометрической каждое значение признака ( ) представляет собой относительный показатель динамики – коэффициент роста, построенный в виде цепной величины (отношение каждого уровня динамического ряда к предыдущему).

4. Средняя квадратическая – применяется при изучении вариации признака. Получается при подстановке в формулы среднестепенной (5.1) и (5.2) коэффициента k=2.

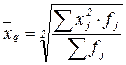, . (5.13)

Важно! Правило мажорантности средних величин: численное значение средних величин возрастает с ростом показателя степени k в формуле среднестепенной функции. Таким образом, .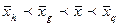

Наиболее часто используемыми видами средних показателей являются средняя арифметическая простая и взвешенная, средняя геометрическая.

Дата добавления: 2014-01-15