Пример. 1 этап. На основании рисунка 10.1 предположим, что связь между стажем работы и уровнем оплаты труда рабочих описывается линейным уравнением регрессии

1 этап. На основании рисунка 10.1 предположим, что связь между стажем работы и уровнем оплаты труда рабочих описывается линейным уравнением регрессии .

2 этап. Для расчета коэффициентов a₀, a₁ построим таблицу вспомогательных расчетов 8.4.

Таблица 8.4.

Таблица вспомогательных расчетов для уравнения регрессии

№ рабочего	№ рабочего п/п i	Стаж работы рабочего, лет xi	Среднемесячный уровень оплаты труда, тыс. руб. yi	Вспомогательные расчеты
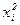
xi ∙ yi		Выровненные значения по уравнению прямой
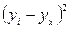
			3,5			3,445	0,0030
			3,7			3,445	0,0649
			3,8			3,445	0,1259
			3,5			3,445	0,0030
			3,7			3,445	0,0649
			3,5	3,5		3,841	0,1161
			3,8	3,8		3,841	0,0017
			3,9	3,9		3,841	0,0035
			4,1	8,2		4,236	0,0186
			4,5			4,236	0,0695
			4,1	8,2		4,236	0,0186
			4,1	8,2		4,236	0,0186
			4,6	13,8		4,632	0,0010
			4,6	13,8		4,632	0,0010
			4,7	14,1		4,632	0,0046
			4,7	14,1		4,632	0,0046
			4,7	14,1		4,632	0,0046
			4,6	13,8		4,632	0,0010
			3,7	11,1		4,632	0,8684
			4,7	14,1		4,632	0,0046
			4,9	19,6		5,027	0,0162
			4,7	18,8		5,027	0,1072
			4,9	19,6		5,027	0,0162
			4,5			5,027	0,2782
			4,5			5,027	0,2782
			5,0			5,423	0,1789
			5,2			5,423	0,0497
			6,0			5,423	0,3329
			6,3	31,5		5,423	0,7692
			6,5	32,5		5,423	1,1600
	Сумма			392,7			4,585
	Среднее	2,67	4,5	13,09	–	4,5	0,164

Составим систему нормальных уравнений:

Решив систему уравнений, получаем значения параметров:

=3,445; =0,396.

Таким образом, уравнение связи принимает вид: . Подставляя в него поочередно все значения стажа работы x_i, получаем теоретические значения оплаты труда (выровненные по уравнению прямой) (графа 3 таблицы 8.4). Правильность произведенных расчетов подтверждает тот факт, что сумма теоретических уровней ряда равна сумме фактических уровней:

135 тыс. руб.

Параметр –коэффициент регрессии – показывает, что при изменении стажа работы на 1 год средний размер оплаты труда увеличивается в среднем на 0,396 тыс. руб. (396 руб.).

Коэффициент эластичности показывает, что при увеличении стажа работы на 1% размер оплаты труда увеличивается в среднем на 0,23%.

Оценим среднюю квадратическую ошибку уравнения регрессии ():

тыс. руб.,

где s – число параметров уравнения регрессии (для уравнения прямой s = 2).

Поскольку < s_у (s_у =тыс. руб.), то использование данного уравнения регрессии является целесообразным.

Отдельно оценим средние квадратические ошибки параметров уравнения регрессии по формулам (10.6):

тыс. руб.; тыс. руб./год,

где (лет);

Нанесем фактические и теоретические значения оплаты труда, а также линию среднего размера оплаты труда на график (рис. 8.2).

Рис. 8.2. Эмпирические линии регрессии фактических и теоретических значений
оплаты труда рабочих в зависимости от стажа работы, постоянная средняя линия

Как видно из рисунка 8.2, переменная средняя сильно отличается от постоянной средней, что говорит о значительном влиянии фактора х (стажа работы) на результативный признак y (уровень оплаты труда). Однако несовпадение линии теоретических и фактических значений уровня оплаты говорит о том, что связь между стажем и уровнем оплаты труда не функциональная (не полная).

Измерим, насколько связь близка к функциональной.

3 этап. Измерение тесноты связи

Рассчитаем все виды дисперсий:

- общая дисперсия, измеряющая общую вариацию результативного признака за счет действия всех факторов:

- факторная (теоретическая) дисперсия, измеряющая вариацию результативного признака у за счет действия факторного признака х:

- остаточная дисперсия, характеризующая вариацию признака у за счет всех факторов, кроме х (т.е. при исключенном х):

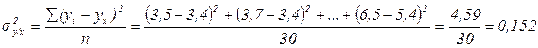
Проверим, выполняется ли правило сложения дисперсий:

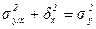0,152 + 0,432 = 0,584 (верно).

Оценим тесноту связи численно с помощью ряда показателей:

1. Коэффициент детерминации:

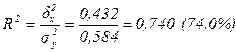- удельный вес вариации результативного признака (уровня отплаты труда), линейно связанной с вариацией факторного признака (стажа работы), составляет 74%.

2. Индекс корреляции (теоретическое корреляционное отношение) составляет:

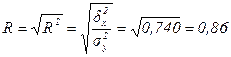- поскольку численное значение индекса корреляции больше 0,7, то линейная связь между стажем работы и уровнем оплаты труда рабочих тесная.

3. Линейный коэффициент корреляции:

,

где ;

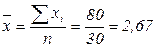(лет); тыс. руб.;

(лет);

тыс. руб.

.

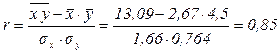Поскольку линейный коэффициент корреляции положителен, то связь между признаками прямая, т.к. он больше 0,7 – связь тесная.

4 этап. Проверка существенности связи с использованием критерия Фишера:

где s – число параметров уравнения регрессии (у прямой два параметра).

В данном примере расчетное значение критерия Фишера F_кр =4,2. Поскольку полученное значение F_расч > F_кр, то существенность линейной связи между стажем работы и размером оплаты труда рабочих подтверждается.

Тема 9. Анализ рядов динамики

1. Ряды динамики и их виды

2. Сопоставимость статистических величин

3. Показатели анализа рядов динамики

4. Приемы анализа и обработки рядов динамики

5. Проверка ряда динамики на наличие тренда

6. Изучение сезонных колебаний в ряду динамики

Дата добавления: 2014-01-15