Последовательность. Предел последовательности

Тема III. ПРЕДЕЛЬНОЕ ИСЧИСЛЕНИЕ

Определение 3.1. Если каждому натуральному числу 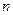поставить в соответствие по некоторому правилу вещественное число 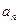, то полученное множество пронумерованных вещественных чисел 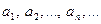называется числовой последовательностью. Числа 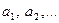называются элементами последовательности, а число 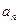- общим (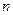- м) членом последовательности.

Пример 3.1. а) - арифметическая прогрессия; б) -1, 1, -1, …, ,… - геометрическая прогрессия; в) 1, 1/2, 1/3, …, ,…; г) -1, 2, -3, …, , ….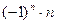

Виды последовательностей

Определение 3.2. Последовательность называется ограниченной сверху (снизу), если 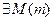такое, что .

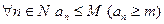Определение 3.3. Последовательность называется ограниченной, если 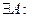(т.е. ограниченна и сверху, и снизу - 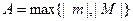). Последовательность называется неограниченной, если .

!Прочитать формулы словами!

Пример 3.2. Последовательность а) является ограниченной снизу (), последовательность б) – снизу и сверху (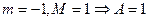), последовательность в) – снизу и сверху (), последовательность г) – неограниченная.

Определение 3.4. Последовательность называется бесконечно большой, если

.

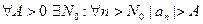Замечание. Любая бесконечно большая последовательность является неограниченной. Обратное, однако, неверно. Так, например, последовательность с общим членом 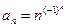неограниченная, но не бесконечно большая.

Определение 3.5. Последовательность называется бесконечно малой, если

.

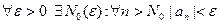Пример 3.3. Последовательности а) и г) являются бесконечно большими, последовательность в) - бесконечно малой.

Свойства бесконечно малых последовательностей

Теорема 3.1. Пусть и - бесконечно малые последовательности, 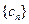- ограниченная последовательность. Тогда последовательност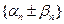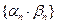и , и 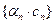также являются бесконечно малыми.

Доказательство. 1) Пусть и - бесконечно малые последовательности, тогда

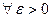
и .

Выберем 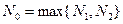, тогда

,

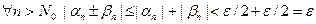то есть последовательность 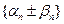является бесконечно малой.

2) Пусть и - бесконечно малые последовательности, тогда

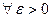
и .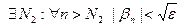

Выберем 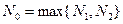, тогда

,

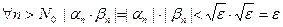то есть последовательность 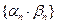является бесконечно малой.

3) Пусть - бесконечно малая последовательность, 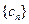- ограниченная. В силу последнего утверждения

.

Поскольку - бесконечно малая, то

.

Тогда

,

то есть последовательность 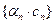является бесконечно малой.

Теорема 3.2 (о связи бесконечно большой и бесконечно малой последовательностей). Если - бесконечно большая последовательность и все её члены отличны от нуля, то последовательность 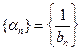является бесконечно малой.

Доказательство. Пусть - бесконечно большая последовательность. По определению . Тогда 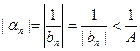. Обозначим и получим, что

,

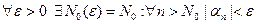то есть последовательность является бесконечно малой.

Сходящиеся последовательности и их свойства

Определение 3.6. Число 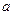называется пределом последовательности , если последовательность является бесконечно малой. Обозначается

.

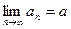Последовательность, у которой есть предел, называется сходящейся.

Из определения предела и свойств бесконечно малых последовательностей вытекают

Теорема 3.3. Сходящаяся последовательность ограничена.

Замечание. Обратное утверждение не верно. Так, например, последовательность б) является ограниченной, но не является сходящейся.

Теорема 3.4. Сходящаяся последовательность имеет только один предел.

Теорема 3.5. Пусть и - сходящиеся последовательности с пределам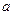и и 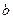соответственно. Тогда последовательности 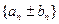, , также являются сходящимися и , , .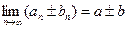

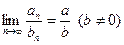Определение 3.7. Последовательность называется возрастающей (убывающей, неубывающей, невозрастающей), если таких, что 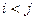, имеет место неравенство (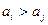, , 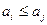). Общее название таких последовательностей – монотонные. Другими словами, последовательность называется монотонной, если последовательность сохраняет знак.

Теорема 3.6. Монотонная ограниченная последовательность является сходящейся.

Дата добавления: 2014-01-15