Алгоритм разработки модели

Модели, применяемые в исследовании экономических систем управления и их классификация.

Современная экономическая теория, как на микро-, так и на макроуровне, включает как естественный, необходимый элемент математические модели и методы. Использование математики в эко­номике позволяет, во-первых, выделить и формально описать на­иболее важные, существенные связи экономических переменных и объектов: изучение столь сложного объекта предполагает высокую степень абстракции. Во-вторых, из четко сформулированных ис­ходных данных и соотношений методами дедукции можно получать выводы, адекватные изучаемому объекту в той же мере, что и сде­ланные предпосылки. В-третьих, методы математики и статистики позволяют индуктивным путем получать новые знания об объекте: оценивать форму и параметры зависимостей его переменных, в наи­большей степени соответствующие имеющимся наблюдениям. На­конец, в-четвертых, использование языка математики позволяет точно и компактно излагать положения экономической теории, формули­ровать ее понятия и выводы.

Математические модели использовались с иллюстративными и исследовательскими целями еще Ф. Кенэ (1758 г., "Экономическая таблица"), А. Смитом (классическая макроэкономическая модель), Д. Рикардо (модель международной торговли). В XIX веке большой вклад в моделирование рыночной экономики внесла математичес­кая школа (Л. Вальрас, О. Курно, В. Парето, Ф. Эджворт и др.). В XX веке математические методы моделирования применялись очень широко, с их использованием связаны практически все работы, удос­тоенные Нобелевской премии по экономике (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон и др.). Развитие микроэкономики, макроэ­кономики, прикладных дисциплин связано с более высоким уровнем их формализации. Основу для этого заложил прогресс в области прикладной математики - теории игр, математического про­граммирования, математической статистики. В России в начале XX века большой вклад в математическое моделирование экономики внесли В.К. Дмитриев и Е.Е. Слуцкий. В 1930-е - 50-е годы в этой области не наблюдалось прогресса вследствие идеологических огра­ничений тоталитарного режима. В 1960-е - 80-е годы экономико-математическое направление возродилось (В.С. Немчинов, В.В. Но­вожилов, Л.В. Канторович), но было связано, в основном, с попытками формально описать "систему оптимального функционирования социалистической экономики" (Н.П. Федоренко, С.С. Ша­талин и др.). Строились многоуровневые системы моделей народно­хозяйственного планирования, оптимизационные модели отраслей и предприятий. Сейчас важной задачей является моделирование про­цессов переходного периода.

Любое экономическое исследование всегда предполагает объеди­нение теории (экономической модели) и практики (статистических данных). Мы используем теоретические модели для описания и объ­яснения наблюдаемых процессов и собираем статистические данные с целью эмпирического построения и обоснования моделей.

Для изучения различных экономических явлений экономисты используют их упрощенные формальные описания, называемые экономическими моделями.

Модель – это копия реального объекта, обладающая его основными характеристиками и способная имитировать его поведение.

Построение модели помогает привести сложные и подчас непреодолимые факторы, связанные с проблемой принятия решения, в логически стройную схему, доступную для детального анализа. Такая модель позволяет выявить альтернативы решения задачи и оценить результаты, к которым они приводят, а также дает возможность определить, какие данные необходимы для оценки имеющихся альтернатив. В итоге это обеспечивает получение обоснованных выводов. Короче говоря, модель является средством формирования четкого представления о действительности.

Примерами экономических моделей являются модели потребительского выбора, модели фирмы, модели экономического роста, модели равновесия на товарных, факторных и финансовых рынках и многие другие. Строя модели, экономисты выявляют существенные факторы, определяющие исследуемое яв­ление и отбрасывают детали, несущественные для решения постав­ленной проблемы. Формализация основных особенностей функцио­нирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

Как обычно строится экономическая модель?

1. Формулируются предмет и цели исследования.

2. В рассматриваемой экономической системе выделяются струк­турные или функциональные элементы, соответствующие дан­ной цели, выявляются наиболее важные качественные характе­ристики этих элементов.

3. Словесно, качественно описываются взаимосвязи между элемен­тами модели.

4. Вводятся символические обозначения для учитываемых характе­ристик экономического объекта и формализуются, насколько возможно, взаимосвязи между ними. Тем самым, формулируется математическая модель.

5. Проводятся расчеты по математической модели и анализ полу­ченного решения.

Следует различать математическую структуру модели и ее содер­жательную интерпретацию. Рассмотрим следующие два простых примера.

Пример 1. Пусть требуется определить, какую сумму следует пол­ожить в банк при заданной ставке процента (20% годовых), чтобы через год получить $12000?

Вводя формальные обозначения для величин, фигурирующих в задаче:

начальная сумма денег – M ₀,

конечная сумма денег – M ₁,

ставка процента - R

и записывая соотношение между ними

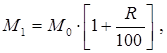
найдем требуемую величину из решения основного уравнения модели

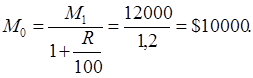
Пример 2. Пусть требуется определить, каков был объем выпус­ка продукции завода, если в результате технического перевооруже­ния средняя производительность труда увеличилась на 20%, и завод стал выпускать 12000 единиц продукции.

Вводя формальные обозначения для величин, фигурирующих в задаче:

начальный выпуск –Q₀,

конечный выпуск – Q₁,

процент прироста производительности - R,

и записывая соотношение между ними (следующее из определе­ния средней производительности труда )

найдем искомую величину из решения основного уравнения мо­дели

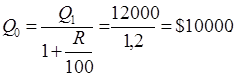
Сравнивая полученные модели и результаты, мы можем заме­тить, что математическая форма модели

и даже числовые значения входящих в нее величин в обоих случаях одинаковы, однако экономическая ситуация, описываемая моделью, экономическая интерпретация модели и результатов рас­чета совершенно различны. Таким образом, одни и те же математи­ческие модели и методы могут быть использованы для решения совершенно различных экономических задач.

Экономические модели позволяют выявить особенности функ­ционирования экономического объекта и на основе этого предска­зывать будущее поведение объекта при изменении каких-либо па­раметров. Предсказание будущих изменений, например, повышение обменного курса, ухудшение экономической конъюнктуры, паде­ние прибыли может опираться лишь на интуицию. Однако при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияю­щие на рассматриваемую ситуацию. В модели все взаимосвязи пе­ременных могут быть оценены количественно, что позволяет полу­чить более качественный и надежный прогноз.

Для любого экономического субъекта возможность прогнозиро­вания ситуации означает, прежде всего, получение лучших резуль­татов или избежание потерь, в том числе и в государственной поли­тике.

По своему определению любая экономическая модель абстракт­на и, следовательно, неполна, поскольку выделяя наиболее сущест­венные факторы, определяющие закономерности функционирова­ния рассматриваемого экономического объекта, она абстрагируется от других факторов, которые, несмотря на свою относительную ма­лость, все же в совокупности могут определять не только отклоне­ния в поведении объекта, но и само его поведение. Так, в простей­шей модели спроса считается, что величина спроса на какой-либо товар определяется его ценой и доходом потребителя. На самом же деле на величину спроса оказывает также влияние ряд других фак­торов: вкусы и ожидания потребителей, цены на другие товары, воздействие рекламы, моды и так далее. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказыва­ют на объект относительно малое результирующее воздействие в интересующем нас аспекте. Состав учтенных в модели факторов и ее структура могут быть уточнены в ходе совершенствования модели.

Математическая модель экономического объекта - это его гомо­морфное отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Гомоморфное отображение объ­единяет группы отношений элементов изучаемого объекта в анало­гичные отношения элементов модели. Иными словами, модель -это условный образ объекта, построенный для упрощения его ис­следования. Предполагается, что изучение модели дает новые зна­ния об объекте, либо позволяет определить наилучшие решения в той или иной ситуации.

Для описания основных видов элементов экономической моде­ли рассмотрим конкретную ситуацию и построим соответствующую ей модель.

Пусть имеется фирма, выпускающая несколько видов продук­ции. В процессе производства используются три вида ресурсов: обо­рудование, рабочая сила и сырье; эти ресурсы однородны, количес­тва их известны и в данном производственном цикле увеличены быть не могут. Задан расход каждого из ресурсов на производство единицы продукции каждого вида. Заданы цены продуктов. Нужно определить объемы производства с целью максимизации стоимости произведенной продукции (или, в предположении, что вся она на­йдет сбыт на рынке - общей выручки от реализации).

Для решения поставленной задачи нужно построить математи­ческую модель, наполнить ее информацией, а затем провести по ней необходимые расчеты. Вначале при построении модели нужно определить индексы, экзогенные и эндогенные переменные и пара­метры. В нашей задаче свой индекс должен иметь каждый вид про­дукции (пусть это индекс i, меняющийся от 1 до n), а также вид ресурсов (если мы обозначаем их одной переменной; пусть в нашей задаче ресурсы обозначены разными переменными). Далее опишем эндогенные переменные - те, которые задаются вне модели, т.е. известны заранее, и параметры - это коэффициенты уравнений мо­дели. Часто экзогенные переменные и параметры в моделях не раз­деляют. В рассматриваемой задаче заданы экзогенные переменные - имеющиеся количества оборудования К, рабочей силы L и сырья R; заданы параметры - коэффициенты их расхода на единицу i-й продук­ции k _i, l _i и r _i соответственно. Цены продуктов p _i также известны.

Далее вводятся обозначения для эндогенных переменных - тех, которые определяются в ходе расчетов по модели и не задаются в ней извне. В нашем случае - это неизвестные объемы производства продукции каждого i-го вида; обозначим их х _i.

Закончив описание переменных и параметров, переходят к фор­мализации условий задачи, к описанию ее допустимого множества и целевой функции (если таковая имеется). В нашей задаче допус­тимое множество - это совокупность всех вариантов производства, обеспеченных имеющимися ресурсами. Оно описывается с помощью системы неравенств:

k ₁ x ₁+ k ₂ x ₂ + … + k _n x _n ≤ K, ∑ k _i x _i ≤ K,

l ₁ x ₁ + l ₂ x ₂ + … + l _n x _n ≤ L, или ∑ l _i x _i ≤ L,

r ₁ x ₁ + r ₂ x ₂ + … + r _n x _n ≤ R, ∑ r _i x _i ≤ R.

К этим ограничениям по ресурсам добавляются требования не­отрицательности переменных x _i ≥ 0. Если бы какой-то ресурс нужно было израсходовать полностью (например, полностью занять всю рабочую силу), соответствующее неравенство превратилось бы в урав­нение. Это сузило бы допустимое множество и, возможно, исклю­чило бы из него первоначально наилучшее решение.

Если модель является оптимизационной (а данная модель тако­ва), то наряду с ограничениями должна быть выписана целевая фун­кция, т.е. максимизируемая или минимизируемая величина, отра­жающая интересы принимающего решение субъекта. Для данной задачи максимизируется величина

p ₁ x ₁ + p ₂ x ₂ + … + p _n x _n , или ∑ p _i x _i max.

Поставленная задача далеко не всегда хорошо описывает ситуа­цию и соответствует задачам лица, принимающего решение (ЛПР). В действительности, по крайней мере:

1) ресурсы до некоторой степени взаимозаменяемы;

2) затраты ресурсов не строго пропорциональны выпуску (есть постоянные затраты, не связанные с объемом выпуска; предельные затраты меняются);

3) объемы ресурсов не строго фиксированы, они могут поку­паться и продаваться, браться или сдаваться в аренду;

4) внутри каждого вида ресурсов можно выделить составляю­щие, функционально или качественно различные, в той или иной мере заменяющие или дополняющие друг друга и по-разному влия­ющие на объем выпуска;

5) цена продукта может зависеть от объема его реализации, то же касается цены ресурса;

6) фирма может использовать одну из конечного набора техно­логий (или сочетание нескольких таких технологий), характеризу­ющихся определенными сочетаниями используемых ресурсов;

7) различные единицы получаемой прибыли могут иметь разную ценность для лица, принимающего решение (что обусловлено, на­пример, особенностями налоговой системы);

8) интересы и предпочтения субъекта не ограничиваются макси­мизацией объема прибыли, поэтому целевая функция должна учи­тывать и другие количественные и качественные показатели;

9) для субъекта реально решаемая задача не ограничивается од­ним моментом или периодом времени, важны динамические взаи­мосвязи;

10) на ситуацию могут воздействовать случайные факторы, ко­торые необходимо принять во внимание.

Многие разделы экономической теории посвящены изучению, описанию и моделированию перечисленных аспектов на различных уровнях хозяйственной деятельности, с той или иной степенью де­тализации и в различных сочетаниях.

Модели, используемые в экономике, можно под­разделять на классы по ряду признаков, относящихся к особеннос­тям моделируемого объекта, цели моделирования и используемого инструментария (рис.1): модели макро- и микроэкономические, теорети­ческие и прикладные, оптимизационные и равновесные, статичес­кие и динамические.

Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финан­совые показатели: потребление, инвестиции, занятость, про­центную ставку, количество денег и другие.

Рис.1. Классификация экономических моделей

Микроэкономические модели описывают взаимодействие структурных и функциональ­ных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде. Вследствие разнообразия типов экономических элементов и форм их взаимодействия на рынке, микроэкономическое моделирование занимает основную часть эко­номико-математической теории. Наиболее серьезные теоретические результаты в микроэкономическом моделировании в последние годы получены в исследовании стратегического поведения фирм в усло­виях олигополии с использованием аппарата теории игр.

Теоретические модели позволяют изучать общие свойства эко­номики и ее характерных элементов дедукцией выводов из формальных предпосылок.

Прикладные модели дают возможность оце­нить параметры функционирования конкретного экономического объекта и сформулировать рекомендации для принятия практичес­ких решений. К прикладным относятся прежде всего эконометрические модели, оперирующие числовыми значениями экономичес­ких переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений.

В моделировании рыночной экономики особое место занимают равновесные модели. Они описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести ее из данно­го состояния, равна нулю. В нерыночной экономике неравновесие по одним параметрам (например, дефицит) компенсируется други­ми факторами (черный рынок, очереди и т.п.). Равновесные модели дескриптивны, описательны.

В нашей стране долгое время преобла­дал нормативный подход в моделировании, основанный наопти­мизации. Оптимизационные модели позволяют определять оптимальные варианты моделируемого процесса из множества альтернативных вариантов, для чего необходимо наличие критерия (системы критериев) оптимизации и эффективной процедуры поиска его экстремального значения. Оптимизация в теории рыночной экономики присутству­ет в основном на микроуровне (максимизация полезности потреби­телем или прибыли фирмой); на макроуровне результатом рацио­нального выбора поведения экономическими субъектами оказыва­ется некоторое состояние равновесия.

В моделях статических описывается состояние экономического объекта в конкретный момент или период времени.В них обычно зафиксированы значения ряда величин, явля­ющихся переменными в динамике, - например, капитальных ресур­сов, цен и т.п.

Динамические модели включают взаимосвязи переменных во времени. Динамическая модель не сводится к простой сумме ряда статических, а описывает силы и взаимодействия в экономике, определяющие ход процессов в ней. Динамические модели обычно используют аппарат дифференциальных и разностных уравнений, вариационного исчисления. В зависимости от того, работает модель в системах реального времени или предназначена для прогнозирования перспектив развития процессов, различают соответственно: модели реального времени и экстраполяционные модели.

Детерминированные модели предполагают жесткие функциональ­ные связи между переменными модели.

Стохастические модели допускают наличие случайных воздействий на исследуемые показа­тели и используют инструментарий теории вероятностей и матема­тической статистики для их описания.

Выбор показателя эффективности

Определение исходных данных

I этап

Построение

Принятие допущений и ограничений

концептуальной

модели

Выбор типа математической модели

Разработка математической модели

II этап

Разработка алгоритмической модели

Разработка

математической

Проверка достоверности модели

модели

Выбор вычислительных средств

Выбор языка программирования

III этап

Разработка

Программирование модели

программной

модели

Планирование эксперимента

Серийный расчет на ЭВМ с фиксацией результатов

IV этап

Анализ результатов

Проведение

машинных

экспериментов

Выработка рекомендаций по дальнейшему совершенствованию модели

с моделью

Использование модели в реальной экономической системе

V этап

Применение

модели

Дата добавления: 2014-01-15