
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
S есть PилиS не есть P
|
|
|
|
В суждении “Некоторые варианты денационализации не представляют собой приватизации” субъектом является понятие “варианты денационализации”, предикатом – понятие “приватизация”, логическая связка выражена словами “не представляют собой”, квантор – словом “некоторые”.
Сложными называются суждения, составными частями которых являются простые суждения или их сочетания (например, “Если инвестирование в данную отрасль будет существенно увеличено, то это потребует сокращения инвестирования в другие отрасли”). Сложное суждение может рассматриваться как образованное из нескольких (не менее двух) исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (и – конъюнкция; или – дизъюнкция; либо, либо – строгая дизъюнкция; если, то – импликация; тогда и только тогда, когда – эквивалентность; не – отрицание). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения.
в) формально-логические законы
Закон мышления - это необходимая, устойчивая, повторяющаяся связь между мыслями. Соблюдение законов логики является необходимым, непременным условием достижения истины в процессе конкретного рассуждения.
Логические законы действуют независимо от воли и желания людей. Они являются отражением действительных связей и отношений вещей. Законы логики являются универсальными и необходимыми. Универсальность основных формально-логических законов вытекает из самого существа мышления.
Наиболее простые и необходимые связи между мыслями выражаются в основных формально-логических законах. Эти законы являются основными потому, что в логике они играют особо важную роль, являются наиболее общими, лежат в основе всех многообразных логических операций с понятиями, высказываниями и используются в ходе выведения и обоснования наших знаний.
Основные законы - это наиболее очевидные из всех утверждении логики, являющиеся чем-то вроде аксиом. Они образуют фундамент логики, на который опирается все ее здание. Сами же они ниоткуда не выводятся, да и не нуждаются ни в какой опоре в силу своей исключительной очевидности.
Кроме основных формально-логических законов, отражающих самые важные свойства всякого правильного мышления, существует много не основных законов, которым также должно подчиняться правильное мышление в процессе оперирования отдельными логическими формами. Все эти законы являются для мышления принципами правильного рассуждения. Все вместе они - законы формирования и развития мысли, определяющие формы и методы познания.
Так как логические законы пригодны и в науке, и в повседневной жизни - вообще в любой области мышления, - то их рассматривают вне зависимости от конкретных высказываний и их связей.
· Закон тождества. Формально закон формулируется как, А = А, а содержательно – объем и содержание мысли о каком – либо предмете должны быть строго определены и оставаться постоянными в процессе рассуждения о нем.
Согласно этому закону необходимая логическая связь между мыслями возможна лишь при условии, если всякий раз, когда в рассуждении появляется мысль о каком-либо предмете, мы будем мыслить именно этот предмет и в том же самом содержании.
Каков бы ни был предмет, закон тождества требует, чтобы: а) рассуждая об известном предмете, мы рассуждали именно о нем, а не о другом предмете, только по ошибке принятом за первый; б) включая мысль о предмете в наши рассуждения, мы мыслили этот предмет по одним и тем же признакам. Закон тождества относится ко всякому предмету мысли, о чем бы мы ни мыслили.
Запрет на отождествление различных мыслей представляется очевидным, хотя в процессе рассуждения он нередко нарушается. Это связано с тем, что любая мысль выражается в языке, причем, одна и та же мысль может быть выражена по-разному (например, "Этот комбинат построен в 1961 году" и "Этот комбинат построен в год первого полета в космос нашего соотечественника"). С другой стороны, привести к ошибочному отождествлению различных мыслей может употребление многозначных слов и слов-синонимов и омонимов.
Значит, нужно употреблять слово только в таких сочетаниях, которые делают его однозначным.
· Закон противоречия (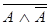 ). Согласно закону противоречия не могут быть сразу истинными два высказывания, из которых одно утверждает нечто о предмете, а другое отрицает то же самое об этом же самом предмете в то же самое время.
). Согласно закону противоречия не могут быть сразу истинными два высказывания, из которых одно утверждает нечто о предмете, а другое отрицает то же самое об этом же самом предмете в то же самое время.
Если мы утверждаем о принадлежности предмету одного признака и в то же время отрицаем принадлежность этому же предмету другого признака, никакого противоречия не будет. Не будет противоречия между высказываниями, если речь идет о разных предметах. Закон противоречия запрещает считать одновременно истинными только такие высказывания, в которых: а) речь идет об одном и том же предмете, б) высказывания относятся к одному и тому же времени, в) утверждения и отрицания рассматривают предмет в одном и том же отношении.
Действие закона противоречия проявляется в стремлении разрешать возникшие противоречия путем уточнения мысли, более строго определяя понятия, отказываясь от некоторых предпосылок. Закон противоречия справедлив относительно всех противоположных друг другу высказываний, независимо от вида самой противоположности.
· Закон исключенного третьего. Формальная запись закона - 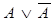 , или содержательно – в процессе рассуждения необходимо доводить дело до определенного утверждения или отрицания, в этом случае истинным оказывается одно из двух отрицающих друг друга суждений.
, или содержательно – в процессе рассуждения необходимо доводить дело до определенного утверждения или отрицания, в этом случае истинным оказывается одно из двух отрицающих друг друга суждений.
Могут ли противоположные друг другу высказывания оказаться оба сразу ложными? Чтобы ответить на этот вопрос, необходимо, в отличие от случая с законом противоречия, уточнить сам характер противоположности, о которой идет речь в конкретном случае.
Если противоположность устанавливается между самыми крайними из всех возможных высказываний относительно одного и того же предмета, то они могут оба оказаться сразу ложными. Если одно утверждает, что все совместные предприятия прибыльные, а другое - что ни одно совместное предприятие прибыльным назвать нельзя, то нельзя представить себе между обоими этими высказываниями противоположность большую, чем та, которую они выражают.
Однако надо помнить: не всегда крайне противоположные высказывания оба одновременно ложные. Они становятся одновременно ложными только тогда, когда между крайними случаями имеются случаи, образующие переход между ними. Для нашего примера таким случаем будет высказывание, что "Некоторые совместные предприятия прибыльные (не прибыльные)". Если это высказывание истинно, то противоположные ему оба ранее названных высказываний одновременно ложные.
Если противоположность между двумя высказываниями не крайняя, то в любом случае такие два высказывания не могут быть оба сразу ложными. Например, в паре высказываний "Все виды доходов облагаются налогом" и "Некоторые виды доходов не облагаются налогом" оба сразу никогда не окажутся ложными, какое бы значение истинности мы ни приписывали любому из них.
Наконец, если оба высказывания относятся к одному и тому же единичному предмету, например: "Эта фирма обанкротилась" и "Эта фирма не обанкротилась", - то относительно них также невозможно предположить одновременную ложность.
В тех случаях, когда одновременная ложность двух противоположных высказываний невозможна, в силу вступает закон исключенного третьего. Согласно этому закону из двух противоречащих друг другу утверждений об одном и том же предмете одно утверждение - и только одно - с необходимостью должно быть признано истинным, так что невозможно никакое третье истинное утверждение об одном и том же предмете.
· Закон достаточного основания. Согласно этому закону для того, чтобы признать высказывание о предмете истинным, должно быть указано достаточное основание.
Этот закон не может указать, каким именно должно быть основание в каждом отдельном случае. Он выражает только мысль, что для всякого истинного утверждения существует и потому должно быть указано такое основание, в силу которого это утверждение является истинным.
Достаточным основанием мыслей может быть личный опыт человека, предшествующий опыт других людей, всего человечества а также любая уже проверенная и признанная истинной мысль из которой с необходимостью вытекает истинность данной мысли. Под достаточным основанием истинности некоторого высказывания вообще понимается совокупность истинных высказываний, таких, что обосновываемое высказывание следует из них по законам и правилам логики.
Только вся совокупность обстоятельств или условий, необходимых и достаточных для возникновения явления, составляет основания этого явления. Поэтому закон достаточного основания подчеркивает необходимость исчерпывающего учета всех необходимых составных частей оснований. Значение закона достаточного основания становится очевидным во всех случаях, когда этот закон нарушается.
г) умозаключение – это форма мышления, в которой из одного или нескольких истинных суждений на основании определенных правил вывода получается новое суждение, которое достоверно или с определенной степенью вероятности следует из них. Суждения, из которых выводится последнее суждение, называются посылками. Суждение, которое выводится из предыдущих суждений, называется заключением.
Умозаключения могут строится по одной из следующих схем:
1. Без В нет С. 2. Все С есть В. 3. Если С, то В.
Без С нет А. Все А есть С. Если А, то С.
 |  | ||||
 | |||||
Без В нет А. Все А есть В. Если А, то В.
где горизонтальная черта означает “следовательно”.
Пример (2). Административные приемы (С) полезны, когда направлены на защиту национальных интересов (В). Лицензирование экспорта (А) относится к административным приемам (С). Следовательно, лицензирование экспорта (А) оказывается полезным, когда направлено на защиту национальных интересов (В).
Пример (3). Если металл нагревается (С), то он расширяется (В).
Если металл подвергается трению (А), то он нагревается (С).
Если металл подвергается трению (А), то он расширяется (В).
Существует следующая классификация умозаключений:
 умозаключения
умозаключения
дедуктивные недедуктивные
индуктивные по аналогии
Дедуктивным называется умозаключение, в котором истинность посылок должна гарантировать истинность заключения. Недедуктивным называется умозаключение, в котором истинность посылок не гарантирует истинности заключения. Индуктивными называются умозаключения, в которых из единичных или частных суждений выводятся общие суждения. Аналогия – это недедуктивное умозаключение, в котором суждение о присущности признака некоторому объекту выводится на основании сходства этого объекта с другим объектом.
Математическая (символическая) логика возникла в результате применения к проблемам формальной логики строгих методов, сходных с теми, которые используются в математике. С помощью специального языка формул достигается адекватное описание логической структуры доказательства и осуществляется построение строгих логических теорий.
Математическая логика базируется на логике высказываний (описание суждений) и ее расширении – логике предикатов (описаниеумозаключений).
Высказывание – предложение, выражающее суждение, которое может быть истинным или ложным.
Высказывания записываются в виде формул, включающих:
1. пропозиционные переменные a, b, …, p, q, … - служащие для обозначения различных понятий;
2. логические знаки:
– или 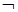 – отрицание;
– отрицание;
 или & - конъюнкция;
или & - конъюнкция;
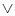 - дизъюнкция;
- дизъюнкция;
→ импликация;
 ↔ эквивалентность;
↔ эквивалентность;


 исключающая (строгая) дизъюнкция.
исключающая (строгая) дизъюнкция.
3. технические знаки: (,) - левая и правая скобки
и строятся по определенным правилам вывода и законам.
Для выяснения истинности или ложности высказываний используют таблицы.
| A | 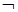 А А
| B | A & B | A 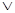 B B
| A ↔ B | A → B |   A B A B
|
| и | л | и | и | и | и | и | л |
| и | л | л | л | и | л | л | и |
| л | и | и | л | и | л | и | и |
| л | и | л | л | л | и | и | л |
где и – истинное значение, а л – ложное.
В логике предикатов дополнительно добавляются:
1. логические знаки
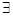 - квантор существования (читается – некоторые, хотя бы один);
- квантор существования (читается – некоторые, хотя бы один);
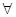 - квантор всеобщности (читается – все, всякие).
- квантор всеобщности (читается – все, всякие).
2. символы предикатов Pi, где i – индекс предиката.
Пример. Пять фирм (A, B, C, D, E) решили упорядочить свое присутствие на товарном рынке и пришли к соглашению:
1. если фирма А присутствует на рынке, то фирма В тоже там присутствует.
2. фирмы С и D могут или одновременно присутствовать на рынке или присутствовать на рынке в отдельности.
3. фирмы В и Е не могут присутствовать на рынке одновременно.
4. фирма Е присутствует на рынке тогда и только тогда, когда на нем присутствует фирма С.
5. если фирма D присутствует на рынке, то фирма А и С также на нем присутствует.
Необходимо определить, какие фирмы в данный момент присутствуют на рынке в соответствии с соглашением.
Введем обозначения:
p – фирма А присутствует на рынке;
q - фирма B присутствует на рынке;
r - фирма E присутствует на рынке;
s - фирма C присутствует на рынке;
t - фирма D присутствует на рынке.
Тогда условия соглашения можно записать:
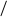
 1. (p → q) 2. (s
1. (p → q) 2. (s 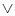 t) 3. (q r) или
t) 3. (q r) или 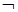 (q ↔ r) 4. (r ↔ s) 5. (t → (p
(q ↔ r) 4. (r ↔ s) 5. (t → (p 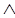 s))
s))
Так как условия соглашения должны выполняться одновременно, можно записать:
(p → q)  (s
(s 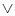 t)
t) 
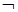 (q ↔ r)
(q ↔ r) 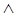 (r ↔ s)
(r ↔ s) 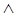 (t → (p
(t → (p 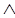 s))
s))
Применяя законы алгебры логики, и заменяя формулы равносильными, можно преобразовать данное выражение к виду:
s 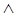 r
r 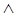
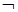 q
q 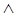
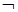 p
p 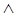
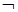 t, то есть на рынке присутствуют только фирмы С и Е.
t, то есть на рынке присутствуют только фирмы С и Е.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 471; Нарушение авторских прав?; Мы поможем в написании вашей работы!