Оптимальное управление

Управление с поиском экстремума.

Объект управления может иметь многоэкстремальную характеристику. V=V1+V2, где V1– быстро, а V2– медленно меняющийся процесс. V1позволяет находит экстремум.

Качество зависит от нескольких факторов: Q=Q(V,y,U), где UЄ u – множество допустимых управлений, V – цель управления, yЄ Y–(множество допустимых выходов).

U*: Q→ extr, при котором UЄ u. Цель управления – нахождение при заданных ограничениях.

6. 6 Адаптивное управление. Сводится к выработке таких управлений, которые наиболее адекватно соответствуют меняющимся условиям и целям управления. Адаптация множество осуществляться как с изменением параметров системы без изменения структуры УУ, так и с изменением структуры и параметров системы. При этом естественно должны быть предусмотрены контуры изменения параметров и структуры. УУ (устройство управления), О (объект) и ВУ (вычислитель параметров) образуют контур изменения структуры и параметров системы.

3. Типовые законы регулирования по отклонению

1.Пропорциональный закон (П – закон).

U=Kp∙E,

где Kp – коэффициент усиления регулятора. Регулятор представляет собой безынерционный усилитель (Еср→ Uср). Данный закон ещё называется также статическим.

Достоинства:

Простота системы. Высокое быстродействие.

Недостатки:

В установившемся режиме имеется не нулевая ошибка (статическая ошибка).

yж→ y0, а для этого U0=const, а значит E0=U0/Kp≠0.

1) Интегральный закон (И – закон).

,

где Ки=1/Tи – коэффициент усиления.

При t>t0 E(t)=0. Это значит что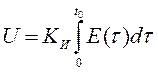

Достоинства:

Отсутствует статическая ошибка E0= 0.

Недостатки:

Медленное быстродействие, большая инерционность.

2) Пропорционально - интегральный закон (ПИ – закон).

,

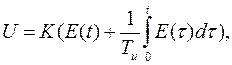где K, Tи, – коэффициент усиления и постоянная времени.

Достоинства:

Позволяет комбинировать астатизм И - закона, и быстродействие П - закона.

Недостатки:

Иногда не может обеспечить необходимое быстродействие.

3) Пропорционально - интегрально - дифференциальный закон (ПИД – закон).

,

где T - постоянная времени дифференцирования. Ки, Кп – коэффициенты усиления от П и И законов.

Достоинства:

Последняя составляющая обеспечивает управление при увеличении скорости возрастания ошибки, позволяя уменьшить её размер.

4) Пропорционально - дифференциальный закон (ПД – закон).

,

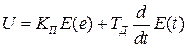где T_д- постоянная времени дифференцирования.

Эти законы являются линейными законами регулирования. Регулятор реализующие эти законы называются аналогично (П - регулятор, И -регулятор и т.д.). Для их реализации на аналоговых элементах требуется ОУ. Учитывая продолжительность работы ориентироваться на ОУ не всегда возможно.

В некоторых случаях целесообразно использовать нелинейные законы. Они позволяют получать свойства системы более предпочтительные по сравнению с линейной зависимостью. Типовые нелинейные законы принято описывать характеристиками нелинейных элементов.

1) Характеристика идеального реле

U=B∙sgn(E), где sgn(E)=E/|E|

2) Реле с зоной нечувствительности

3) Реле с гистерезисом

при ΔU→0

4) Реле общего вида.

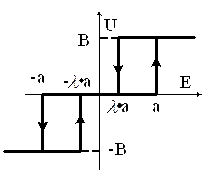
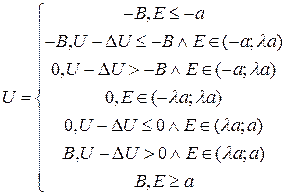при ΔU→0.

Здесь λ – коэффициент возврата. λ Є [-1;1]. Если λ=1 и a=0, то получается идеальное реле.

Подбирая параметры характеристики реле и охватывая её ОС, можно

реализовать любой из выше рассмотренных узлов. Все рассмотренные законы можно считать классическими. В настоящие время применяют и другие законы. Это нeчёткие регуляторы, управление с внутренней моделью.

4. Классификация систем управления

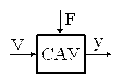
Здесь V– некоторая цель управления. F – возмущения, y – полезная работа.

1) По структуре входного сигнала V.

· V(t)=const – система стабилизации.

· V(t) – известная функция – система программного регулирования.

· V(t) – неизвестная функция, но измеряемая в любой момент времени – следящая система.

2) По характеру сигнала в контуре управления.

· Все сигналы аналоговые – система называется аналоговой, непрерывной или обыкновенной.

· Хотя бы один сигнал дискретный – дискретная система. Под дискретным понимают импульсный и (или) цифровой сигнал. При рассмотрении таких сигналов пренебрегают шагом квантования по амплитуде, принимая цифровой сигнал за импульсный длительностью, равной периоду квантования. Использование дискретной модели сопряжено с несколькими особенностями: все САУ на выходе имеют аналоговый сигнал у(t), обусловленный аналоговыми объектами. Это приводит к тому, что приходится определять дискретную модель аналоговых элементов систем.

3) По свойствам оператора системы.

,

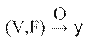где O – оператор.

· Линейный. Систем, описываемыхстрого линейным оператором, не существует. Линейные операторы приближенно описывают динамические свойства системы.

· Нелинейный. Позволяет более полно отразить свойства системы. Для аналоговой системы в качестве нелинейного оператора может служить дифференциальный оператор(в форме дифференциального уравнения). При выборе структуры оператора используются разнообразные упрощения описания системы. Наиболее предпочтительным упрощением является линеаризация оператора – замена нелинейного оператора линейным, эквивалентным в основных параметрах исходному. В результате линеаризации появляется линейная система, а породившую их нелинейную систему называют линеаризуемой. Следует учитывать, что не все системы можно линеаризовать полностью (или даже частично).

В классе линейных систем выделяют:

¾ Непрерывно линейная система – обыкновенная система.

¾ Дискретно линейная система – цифровая или импульсная. Это класс особых систем.

¾ Системы с линейными характеристиками, меняющимися во времени – линейные нестационарные системы. Они описываются дифференциальными уравнениями с переменными коэффициентами.

¾ Системы с распределенными параметрами.

4) По свойствам сигналов F и V.

· Детерминированные функции – детерминированная система.

· Случайные функции – стохастическая система.

· Иногда случайными являются параметры системы – система со случайными параметрами.

5) По способу управления.

Система делят по реализованному в них способу управления. Это: обыкновенная система, реализующая принцип регулирования по отклонению, с поиском экстремума, адаптивная. В каждом из этих классов можно выделить:

· Обыкновенные системы.

· Робастные системы. Предназначены для работы УУ обладающими неполными сведениями о системе (известны лишь границы изменения свойств объекта).

5. Общие сведения о моделях систем.

Модели элементов САР

Основным требованием, предъявляемым к моделям элементов системы, является удобство решения основных задач ТАУ. Прежде чем рассматривать модели элементов целесообразно рассмотреть эти задачи.

Основные задачи ТАУ:

Дата добавления: 2014-01-15