Синтез систем

Анализ систем

Идентификация систем

Построение математической модели поведения системы, отражающей основные свойства системы, в форме, удобной для дальнейшего анализа и синтеза систем. Основная трудность при идентификации системы является определение модели обьекта управления. В общем случае данная задача пока не решена.

Любая математическая модель системы сначала представляет собой набор описаний элементов. Затем общее описание системы получают из описаний элементов

Заключается в исследовании влияния параметров полученной системы на поведение этой системы.

Любая система работает в разнообразных режимах:

a. Установившийся режим. Анализ заключается в исследовании устойчивости установившегося режима (анализ устойчивости).

b. В установившемся режиме возникает задача анализа точности воспроизведения входного сигнала (анализ точности установившегося режима).

c. Переходной режим. Здесь возникает задача оценки качества переходного процессов в системе (анализ качества переходного процесса)

Сводится к разработке системы, удовлетворяющей заранее заданным требованиям качества её поведения.

a. Система должна иметь значения показателей не хуже заданных.

b. Система должна иметь наилучшие свойства среди систем заданного класса.

Идентификация и синтез базируются на результатах анализа системы, но являются более сложными и до конца не решенными задачами.

6. Уравнения элементов САУ

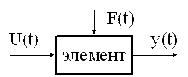Для упрощения составления уравнений всей системы сначала необходимо рассмотреть уравнения элементов, путём решения задачи их идентификации.

Уравнения, описывающие поведение элементов, могут быть получены путём теоретических или экспериментальных исследований, либо их комбинаций. При теоретическом описании законы определяют поведение элементов (законы физики, химии, кинетики). Определяется как структура, так и свойства элементов. Уровень анализа элемента соответствует уровню описания дифференциальными уравнениями с сосредоточенными параметрами (сведёнными в точку). Можно попытаться теоретически описать все законы. Когда теоретически описать не удается, то элементы рассматривают как чёрный ящик.

Уравнение элементов составляются в два этапа.

На первом этапе описываются все особенности элементов, не заботясь о сложности получаемой зависимости. В общем случае это Нелинейные дифференциальные уравнения(ДУ.) Они могут быть представлены как:

а) уравнения вход- выход;

б) уравнения состояний

Урав нение вход- выход имеет вид

y(n)= G(y(n-1),..., y, U(m),...,U, F(n),...F) возмущение m, r≤n.

Рассмотрим вектор 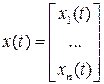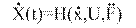– уравнение состояния.

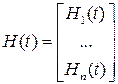Y=R(X,U,F). упрощают

На втором этапе дифференциальные уравнения(ДУ) упрощают. Упрощение состоит в том, что в уравнениях оставляют параметры, отражающие основные особенности поведения данной системы. Так получают упрощенную модель в виде ДУ. Далее полагают, что на её основе можно оценить всевозможные процессы, происходящие в элементе. Наиболее часто нелинейные ДУ упрощают до линейных. Замену нелинейных ДУ линейными называют линеаризацией.

В ТАУ разработано большое число приёмов линеаризации:

– линеаризация на основе гипотезы о малых отклонениях;

– гармоническая линеаризация;

– статистическая линеаризация и.т.д.

7. Линеаризация на основе гипотезы о малых отклонениях

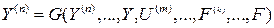–уравнение вход-выход.

В установившимся режиме:

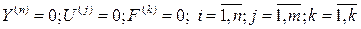
Уравнения статики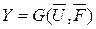

Для линеаризации уравнения динамики представляют виде:

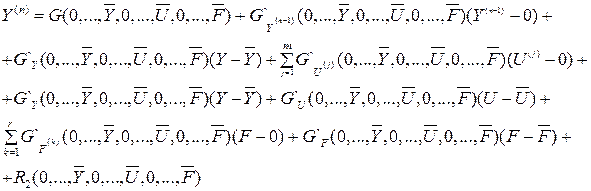
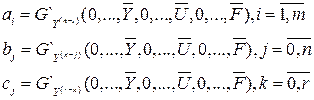
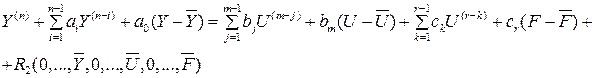
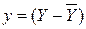– отклонение выхода от установившегося значения.

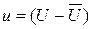– отклонение входа от установившегося значения.

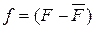– отклонение возмущения о установившегося значения.

При линеаризации ДУ:

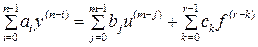
Получили следующие уравнения

при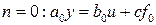

при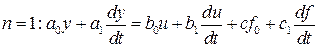

Используем при математическом исследовании ДУ.

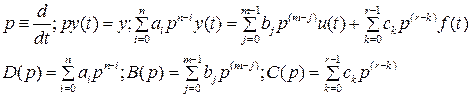
D(p),B(p),C(p) – линейные дифференциальные операторы полиномиального типа.

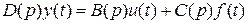
– характеристическое уравнение.

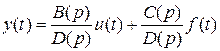
где 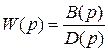– ОПФ по входу 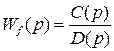– ОПФ по возмущению

Реально при описании ДУ стандартной формы:

1) 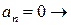все члены ДУ имеют размерность [y]

2) 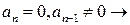все члены ДУ имеют размерность []

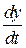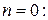
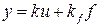где k и kf– коэффициент усиления по входу и по возмущению.

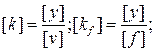
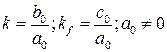
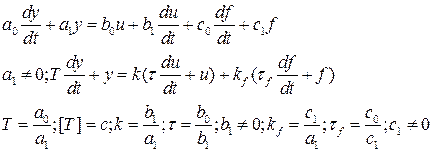
Рассмотрим линеаризацию уравнений состояния

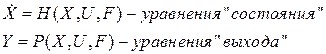
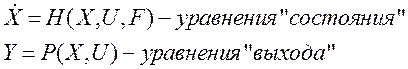
1. Установившийся режим .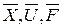

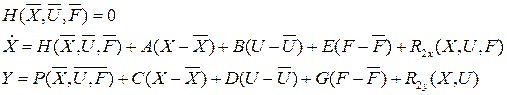
Обозначим отклонения координат от их установившихся значений в виде:

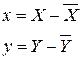
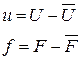
Получим

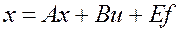
– уравнение состояния

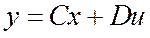
– уравнение выхода.

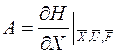– матрица Якоби.

Аналогично

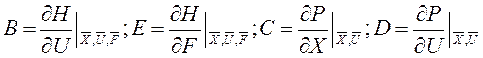
Если каждый из элементов системы описывается ДУ, то это не всегда удобно, т.к нужно искать уравнение входа выход всёей системы. Вместо ДУ рассматривают их алгебраические аналоги, полученные путём алгебраизации ДУ. Обычно алгебраизация осуществляется на основе преобразования Лапласа.

8. Преобразование Лапласа

Преобразование Лапласа определяется для функции оригинала.

f(t) – оригинал, если удовлетворяет условиям:

1)

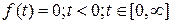
Дата добавления: 2014-01-15