
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Масштабирование
|
|
|
|
Понятие об инвариантности систем.
Система называется инвариантной к внешнему воздействию, если она воспроизводит этот сигнал с нулевой ошибкой, как в переходном, так и в установившемся режиме. Требование равенства нулю ошибки означает, что система должна точно копировать входной сигнал на выходе и иметь нулевую реакцию на возмущение.
Передаточная функция: Ф(S)=1
Передаточная функция по возмущению: Фf(S)=0
 Рассмотрим возможность реализации условия инвариантности в рамках системы с единичной ОС
Рассмотрим возможность реализации условия инвариантности в рамках системы с единичной ОС
Ф(S)=
В некоторых случаях в систему вводят дополнительные связи по управлению для увеличения точности. W(S)= W1(S) W2(S)
Ф(S)=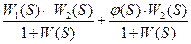
W2(S)(W1(S)+φ(S))=1+ W1(S) W2(S), это возможно, когда:
W2(S) φ(S)=1 или периодическая функция дополнительные связи:
W2 отражает наиболее инерционные элементы системы. Их передаточная функция имеет порядок знаменателя больше порядка числителя.
Нельзя найти физическую реализацию φ(S), которая обеспечит абсолютную инвариантность системы на входное воздействие.
Рассмотрим инвариантность системы при действии возмущения:
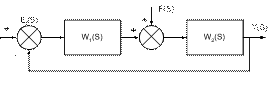
 W2(S)=0
W2(S)=0
Рассмотрим дополнительную связь:  - передаточная функция дополнительной связи
- передаточная функция дополнительной связи
F(S) измеряется с помощью какого-либо датчика
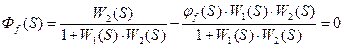
 =
=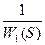 W1(S)=k
W1(S)=k
Если реализовать такую возможность, то получим систему комбинированного регулирования.
В общем случае реализовать комбинированную систему невозможно
Реализуем частичную инвариантность (до Е)
Частичная инвариантность эквивалентна повышению порядка астатизма системы по входу и возмущению. Покажем, что с помощью выбора φ(S) можно статическую систему преобразуют в астатическую II порядка без использования интегральных звеньев.
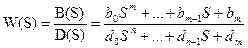 Эта система статическая.
Эта система статическая.
ФЕ(S)=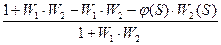
1- φ(S)W2(S)
W2(S)=
(en-Cn1)d0=1
(en-1-Cn1-1)d+(en-Cn)d1=0
W2(S)=C(S)/G(S)
Ф(S)= 
bm=a=n; bm-1=an-1
Такого же эффекта увеличения порядка астатизма можно добиться, если в системе 2 интегральных звена, но при этом система станет неустойчивой, так как изменяется характеристическое уравнение. Введение дополнительных связей не меняет характера уравнения и не влияет на устойчивость.
 2. Повышение порядка астатизма включением интегрального звена.
2. Повышение порядка астатизма включением интегрального звена.

W(S)= T=
T=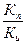

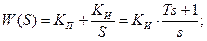

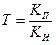
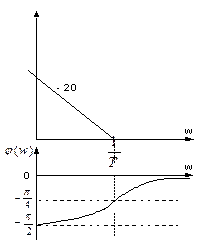
φ(w)=
KП>>KИ Т>>1 w >1/T
ЛЧХ системы не изменяется.
Дальнейшее увеличение точности обеспечивается за счет увеличения коэффициента усиления системы.
А. Масштабирование в прямой цепи
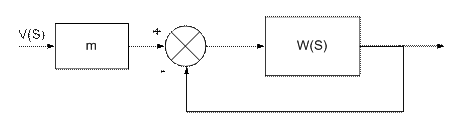
W(S)=KW0(S)
 Ф(S)=
Ф(S)=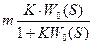 Kз=Ф(0)=
Kз=Ф(0)=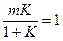 mK=1+K; m=
mK=1+K; m=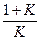
В. Масштабирование в цепи ОС
Ф(0)= 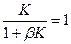
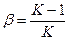
Практически статических систем нет, так как простым масштабированием им даются свойства систем с астатизмом I-го порядка.
48. Анализ качества переходных процессов
1. Понятие о качестве переходных процессов.
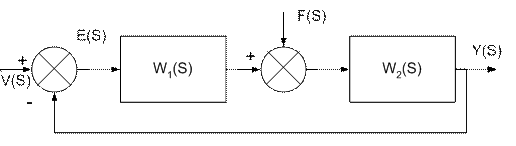
Y(S)=Ф(S)V(S)+ Фf(S)F(S) -изображение вынужденной составляющей.
Если начальные условия не равны 0, то
Y(S)=Ф(S)V(S)+ Фf(S)V(S)+Y(S,Y0),где
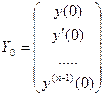
В процессе работы различают ненулевые начальные условия, различные входные сигналы, которых может быть несчетное множество. Качество переходных процессов в системе оценивается по виду её переходной характеристики.
Для анализа качества переходной характеристики рассмотрим входной сигнал.
1)V(t)=1(t)
V(S)=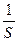
F(t)=0 F(S)=0
Получили изображение переходной характеристики по входу:
Y(S)=H(S)=Ф(S)
h(t)=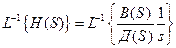
Si –корни характеристического уравнения.
Д(S)=0, i=
h(t)= 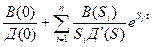
Переходная характеристика является либо типовым, либо неблагоприятным режимом работы системы, в котором проявляются динамические свойства системы
2) V(t)=0
F(t)= 1(t)
Hf(S)=Фf(S)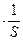 изображение переходной характеристики по возмущению
изображение переходной характеристики по возмущению
hf(t)=L-1{Hf(S)}
49. Показатели качества переходного процесса, определяемые по переходной характеристике.
А) качественные
Б) количественные
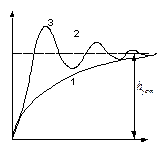 h(t)=hycm при t→∞(t≥tp)
h(t)=hycm при t→∞(t≥tp)
1- монотонная
2- слабоколебательная
3- сильноколебательная
Качественные показатели не позволяют объективно оценивать переходной процесс, особенно на границе между определениями.
Чтобы избежать субъективизм используют количественные показатели.

1. Перерегулирование σ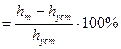
2. Время регулирования tp:(h(t)-hycm) t≥tp
t≥tp
 от hycm
от hycm
Эти два показателя являются основными, они задаются на разработку любой САР
σ≤ σзадан; tp≤ tp задан
3. Время установления ty
4. tm время первого максимума
5. æ -число колебаний за время tp
Чтобы оценивать качество системы разрабатывают многочисленные группы методов анализа качества переходных процессов. Их можно разбить на 2 больших группы:
· Прямые методы
· Косвенные методы.
Прямые методы предполагают определение выделенных показателей качества непосредственно по кривой h(t). К прямым относят методы, позволяющие построить график h(t) или найти для него математическое выражение. Они используются как доказательство, что разрабатываемая система имеет показатели качества не хуже заданных.
Косвенные методы менее трудоёмкие, чем прямые, и позволяют оперативно оценивать выделенные показатели качества. На этапе выбора структуры и параметров системы. Далее рассмотрим эти методы подробнее.
50. Прямые методы.
Прямые методы – методы решения дифференциальных уравнений системы.
W(S)=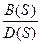
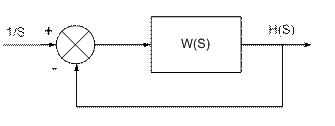
Ф(S)= 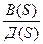
Д(p)h(t)=B(p)1(t)
B(p)=b0p+b1
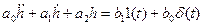
t=0_ h(0)=h`(0_)=0
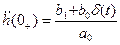
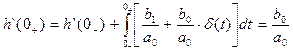
Среди этих методов выделяют:
1) Теорема разложения Хевисайда
Характеристическое уравнение замкнутой системы Д(S)=0
Si=Si(Д); i=
h(t)=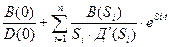 , где
, где 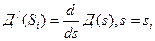 ;
;
2) Классические методы решения дифференциальных уравнений;
3) Использование теоремы разложения;
4) Методы численного решения дифференциальных уравнений (методы моделирования);
5) MATLAB, VISSIM, Mathcad. Используется численное моделирование дифференциальных уравнений
51. Косвенные методы.
Косвенные методы предполагают для оценки показателей качества использование различных характеристических систем, связанных с её переходной характеристикой. Все эти методы можно разбить на две группы:
v Корневые
v Частотные
Корневые предполагают использование корней характеристических уравнений. Они могут выступать в виде нуль-польных портретов системы(комплексная плоскость, на которой отмечены все нули полюсы передаточной функции замкнутой системы) или в виде корневых годографов (траектории, описывающие изменение значения корней характеристического уравнения при изменении одного или нескольких его параметров, например, коэффициента усиления разомкнутой системы.)
Частотные методы используют различные частотные характеристики, например, Р(ω)-вещественная частичная характеристика.
h(t)=
M(ω)-АЧХ замкнутой системы
W(jω)-
W-1(jω)- обратная АФХ разомкнутой системы
L(ω)-ЛЧХ разомкнутой системы
52. Оценка показателей качества по корням.
 Имеется комплексная плоскость с точками, соответствующим корням.
Имеется комплексная плоскость с точками, соответствующим корням.
|-α|=δ=α степень устойчивости
Α позволяет оценить практическое время переходного процесса tp
S1→C1eα t=h1(t)
h(t)=
переходной процесс закончен, если αtp≥3 tp≥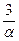
 Если tp≤ tp задан, то
Если tp≤ tp задан, то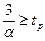 ,
, 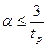
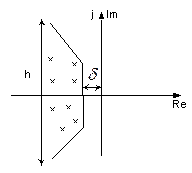 Если S1и S2 мнимые корни, то их величина будет определять δ
Если S1и S2 мнимые корни, то их величина будет определять δ
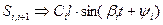 Все составляющие hi(t) будут имеет ограниченную колебательность, если величины βi ограничены в соответствии с αi
Все составляющие hi(t) будут имеет ограниченную колебательность, если величины βi ограничены в соответствии с αi
За какой-то период колебаний hi(t) затухнет.
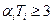 αi2π≥3β βi≤⅔πα
αi2π≥3β βi≤⅔πα
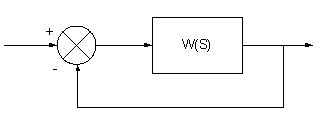 53. Оценка показателей качества по АЧХ замкнутой системы.
53. Оценка показателей качества по АЧХ замкнутой системы.
Ф(jw)= =M(w)ejθ(w)
=M(w)ejθ(w)
M(w) – АЧХ замкнутой системы
Типовое значение АЧХ иллюстрируется следующим графиком:
 wp – резонанасная частота
wp – резонанасная частота
М(wp)=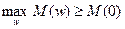
M(0)=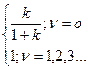 wc – частота среза
wc – частота среза
L(wп) – частота положительности, связанная с wc
wп =(0,6÷0,8)wc
Величина Ммах показывает склонность системы к автоколебанию Ммах→∞
Величина M(w) полностью определяется значениями АФХ разомкнутой системы.
W(jw)=ν (w)+jV(w). Определим линии равных значений М
М(w)=
ν2+V2=M2[(1+ν)2+V2]
ν2(1 -M2)-2 M2 ν+(1 -M2)М2=М2
ν2-2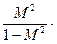 ν+ V2=
ν+ V2=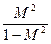
(ν+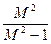 )2+V2=
)2+V2=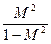 (1
(1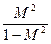 )
)
С=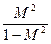 ; R=
; R=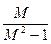
(ν +C)2+V2=R2

Ммах→∞
Ммах≤1.1÷1.5
σ≤60%
Ммах=1; σ=0
54. Оценка показателей качества по ЛАЧХ разомкнутой системы.
Типовая ЛАЧХ, L(w), (L(w),φ(w))
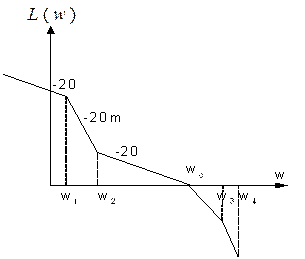 Рассмотрим минимальные фазовые системы, для которой вид одной характеристики определяет другую.
Рассмотрим минимальные фазовые системы, для которой вид одной характеристики определяет другую.
1) СЧ участок (среднечастотный) w<w2,w3c -20дб/дек
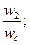
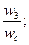
2) НЧ участок w<w1 -20 дб/дек ν=1 – первый порядок астатизма
3) Участок сопряжения НЧ со СЧ участком задается соотношением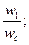 , имеет наклон - 20 mдб/дек, m=1,2,3…
, имеет наклон - 20 mдб/дек, m=1,2,3…
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 435; Нарушение авторских прав?; Мы поможем в написании вашей работы!