
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частотные характеристики замкнутой системы
|
|
|
|

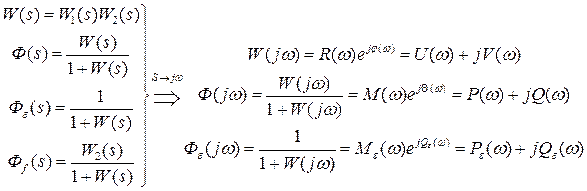
ЧХ позволяют исследовать установившиеся процессы.
Уравнения состояния
В некоторых случаях удобно описывать систему с помощью уравнений состояния. При описании систем и элементов в пространственном состоянийи: рассматриваются векторы: а)  - вектор координат состояния;
- вектор координат состояния;
б) 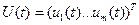 - вектор управлений (входов);
- вектор управлений (входов);
в) 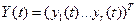 -- вектор выходов.
-- вектор выходов.
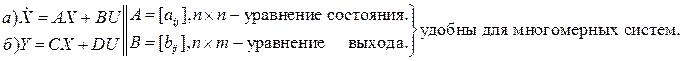
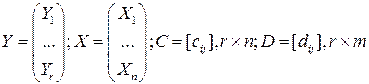
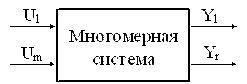 где Ф(S) – матричная передаточная функция.
где Ф(S) – матричная передаточная функция. 
Многомерные системы удобно описывать уравнениями состояния:
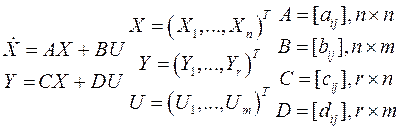
Х – вектор состояния. При использовании нормальной формы Коши записи ДУ  ; U – вектор управления, Y – вектор выхода.
; U – вектор управления, Y – вектор выхода.
A- системная матрица, B – матрица входа, С и D – матрицы выхода. Часто D=0, при этом: 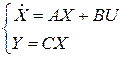 Координаты состояния можно изменять с помощью преобразования подобия матриц:
Координаты состояния можно изменять с помощью преобразования подобия матриц:
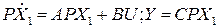
 X
X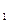 -новые координаты состояния. Уравнения примут вид
-новые координаты состояния. Уравнения примут вид
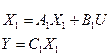

Преобразования подобия не меняют собственные числа матриц.
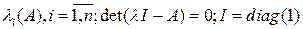
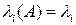 – собственные числа (значения) матрицы А, являющимися корнями характеристического уравнения.
– собственные числа (значения) матрицы А, являющимися корнями характеристического уравнения.
Покажем, что преобразования подобия не меняют собственные числа матрицы


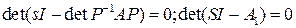 .
.
При исследовании систем используется алгебраизация уравнений состояний с помощью преобразования Лапласа.

X(0) – вектор начальных условий.
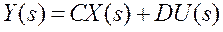
Для определения матричной передаточной функции выразим X(s) из 1-ого уравнения
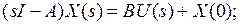


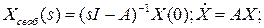
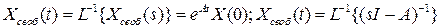
 – матричный экспоненциал- матрица Коши.
– матричный экспоненциал- матрица Коши.
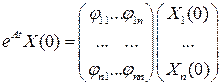
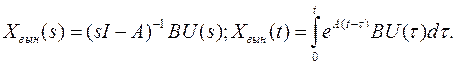
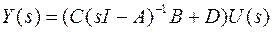
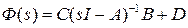 – матричная передаточная функция.
– матричная передаточная функция. 
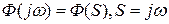 – матричная АФХ системы.
– матричная АФХ системы.
При исследовании системы по уравнениям вход - выход частотные характеристики представлены не только виде АФХ, АЧХ, ФЧХ, но в виде логарифмических характеристик (ЛЧХ). Используют логарифмический масштаб по оси абсцисс и по оси ординат.
20. Логарифмические частотные характеристики
1. Логарифмические масштабы
W(jω)=R(ω)ejφ(ω)
lnW(jω)=lnR(ω)+jφ(ω)
часть завис. завис.
от АЧХ от ФЧХ
В качестве логарифмического масштаба оси частот используется lg ω.

lg2≈0.3 lg3≈0.5 lg5≈0.7
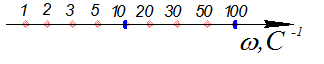
масштаб по осям нелинейный.
L(ω)=20 *lgR(ω)=20 *lg|W(jω)| (дБ)
L(ω)- построенная с использованием логарифмического масштаба частот- называется ЛАЧХ.

Стандартные наклоны используются при построении асимптотических ЛАЧХ.
Фазовая характеристика:
φ(ω), построенная с использованием логарифмического масштаба частот по оси абсцисс и обычного масштаба по оси ординат называется ЛФЧХ-логарифмической фазочастотной характеристикой.
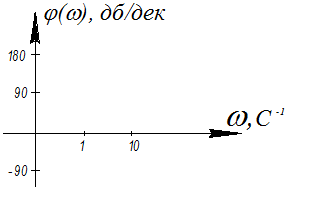
21. Логарифмические характеристики разомкнутой одноконтурной системы.
В этой системе отсутствуют контуры местной ОС.

W5(s)=W2(s)+W3(s)
W(s)=W1(s)∙W5(s) ∙W4(s) W(s)=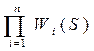 -типовая форма ПФ разомкнутой одноконтурной системы.
-типовая форма ПФ разомкнутой одноконтурной системы.
W(j ω W)=R1(ω)ejφ1(ω)… Rn(ω)ejφn(ω)=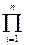 Ri(ω)ejφ(ω)= R(ω)ejφ(ω)
Ri(ω)ejφ(ω)= R(ω)ejφ(ω)
φ(ω)=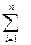 φi(ω); R(ω)=
φi(ω); R(ω)= 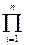 Ri(ω) L(ω)=20lgR(ω)=
Ri(ω) L(ω)=20lgR(ω)= 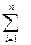 Li(ω)
Li(ω)
Li(ω)=20lgRi(ω); i=1…n φ(ω)==argW(jω)= 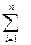 φi(ω
φi(ω
В системе может быть контур с местной ОС:
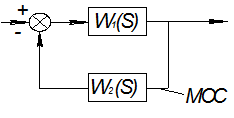
W(jω)=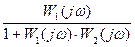 -
-
ПФ соединения с ОС
R(ω)=|W(jω)|= 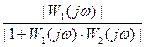
L(ω)=20lgR(ω)=20lg|W1(j ω)|-20lg|1+W1(j ω)W2(j ω)|=L1(ω)-Lk/(ω)
L1(ω)=20lgR1(ω)
Lk/(ω)=20lg|1+Wk(jω)|, где W (j
(j )=W
)=W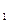 (j ω)W
(j ω)W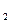 (j ω).
(j ω).
Lk/(ω)=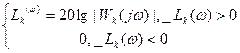
22. ЛЧХ типовых сомножителей
В качестве типовых рассматривают сомножители W1(s)=k/sν; W2(s)=(Ts+1)m,
 = 0;
= 0;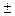 1;
1;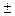 2;…
2;… m=
m=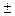 1;
1;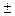 2;…
2;…

W3(s)=(T2s2+2ξTs+1)n, n=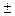 1;
1;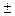 2;…
2;…

АФХ сомножителя первого типа
W1(jω)=k/(jω)ν;
где k- коэффициент усиления, ν- порядок астатизма
k>0; ν=0; ±1; ±2 показатель степени


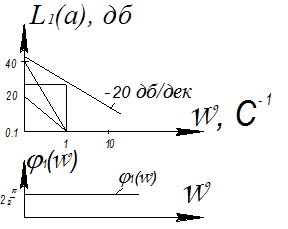 1.W1=30
1.W1=30
L1(l)=20 lg(30)=30 дB

W2(S)=40/s2; 20lg40=32 дВ;  ; ν=2
; ν=2

W3(s)=30 *s; ν=-1
Если изменять K, то все прямые будут подниматься при увеличении K и опускаться при уменьшении K, не изменяя наклона.
б) Cомножитель второго типа имеет ПФ W2(s)=(Тs+1)m
T>0; m=±1; ±2;…
W2(jω)=(1+jωT)m=( )m∙еjm∙arctg(ωT)
)m∙еjm∙arctg(ωT)
j=
L2(ω)=20m∙lg( ). Если задаваться частотой
). Если задаваться частотой
ω € (0, ), то выражение L2(ω) определяет точную ЛАЧХ.
), то выражение L2(ω) определяет точную ЛАЧХ.
Вместо точной удобнее пользоваться асимптотической ЛАЧХ,составленной из отрезков асимптот.
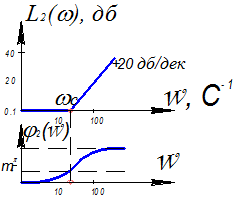
1) Левая асимптота:
ω<1/T, (ωT)2 «1
L2а(ω)= 20m lg =0
=0
2) Правая асимптота:
ω 1/T, (ωT)2 » 1
1/T, (ωT)2 » 1
L2b(ω)= 20m lg =20m lg(ωТ)- прямая с наклоном +20m дB/дек;
=20m lg(ωТ)- прямая с наклоном +20m дB/дек;
φ(ω)= m arctg(ωT).
| ωT | 0.5 | 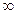
| |||
| aArc tg(ωT) | 23030’ | 450 | 63030| | 900 |
Точная ЛAЧХ L2(ω) будет отличаться от асимптотической, | L2a(ω)-L2( )|
)|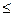 3m дВ
3m дВ
в) W3(sS) = (T2sS2+2ξTsS+1)n; [T]=c; ξ- показатель колебательности, ξ € (0,1). Характеристическое уУравнение
T2sS2+2ξTsS+1=0
иИмеет корни s1,2=-ξ ω0±j ω0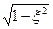 , где ω0=1/T.
, где ω0=1/T.
где ω0=1/T. При ξ>1 характеристический многочлен допускает разложение
T2sS2+2 ξTsS+1=(T1sS+1)(T2sS+1),
Где - 1/T1, -1/ T2 – вещественные корни характеристического уравнения. При ξ=1 => T1=T2. АЧХ
ξ=1 => T1=T2. АЧХ
W3(ω) = 
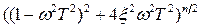

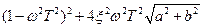



 )n, ФЧХ
)n, ФЧХ
φ3(ω)= n arc tg . ЛАЧХ
. ЛАЧХ
L3(ω)= 20n lg 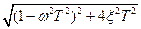


φ3(ω)= n arc tg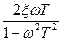
при ω € (0, 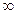 ) определяют точные ЛЧХ.
) определяют точные ЛЧХ.
Асимптоты ЛАЧХ
L3a(ω)= 20m lg 1=0 при ω<1/T; (ωT)2«1
L3б(ω)= 40n lg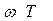 ω>1/T;
ω>1/T; 






 =40 n lg
=40 n lg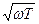
ω>1/T; (

ωT)2»1
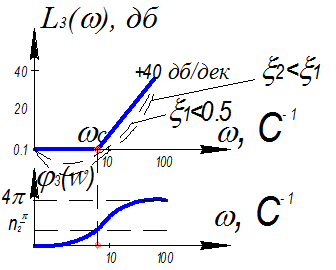 L3(1/T)=20n lg(2ξ)
L3(1/T)=20n lg(2ξ)
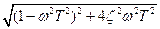
При построении ЛЧХ разомкнутой системы нужно:
1) Построить L(ω)=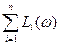
2) φ(ω)=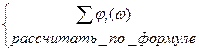 и построить график.
и построить график.
Правило построения асимптотической ЛАЧХ разомкнутой одноконтурной системы:
1. Определяются коэффициент усиления, порядок астатизма и все сомножители 2-го и 3-го типа (к, ν, mk,nk).
2. Для каждого сомножителя определяются сопрягающие чаислтоты:
mMk=>ωk=1/Tk; nk=> ωk=1/Tk - сопрягающие частоты, которые отмечают на оси ω.
ωk1< ωk2< …<ωkN
3) Строится НЧ участок ЛАЧХ ω≤ω1=min ωk1
a) на частоте ω=1 cС-1 откладывается ордината; 20 lgk.
Через полученную точку проводится прямая с наклоном -20 ν д Бб/дек.
Отрезок этой прямой в области НЧ является НЧ участком ЛАЧХ.
4) На каждой из сопрягающих частот наклонной прямой изменяется на 20m дБ/дек, если ωк1 обусловлена сомножителем ->(ТsS+1)m ,
Ллибо на 40n дБ/дек, если=> ωк2 обусловлена сомножителем (Т2 sS2+2ξTsS+1)n
5) При необходимости при малых ξk, в области сопрягающих частот, обусловле-н нных сомножителямиь 3-го типа, в асимптотическую ЛAЧХ вводят поправки..
Примеры:
1) W(s)=10/(2s+1)
W1(s)=10/s0; k=10; ν=0;
ν=0
T=2c; ω=1/2=0,5 c-1

2) W(sS)=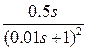
K=0.5; ν=-1; m=-2; T=0.01 c; 20lg0.5=-6 dB.
ω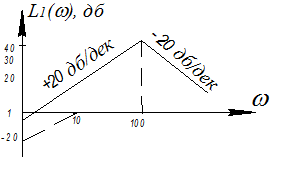 =1/Т=100 c
=1/Т=100 c
φ(ω)=π/2-2arctg(0.01ω)
3) W(sS)=
к=50; 20 lgk=34 дБ;
ν=1; ω1=1/1.4=0.7 c-1; ω2=1/0.5=2 c-1; ω3=1/0.05=20 c-1;.
T=0.05 c; ξ∙0.1=0.07=> ξ=0.7
Звено колебательное.
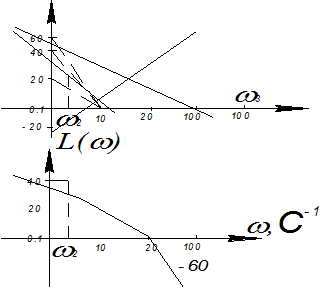 L(ω)≤-30 дб
L(ω)≤-30 дб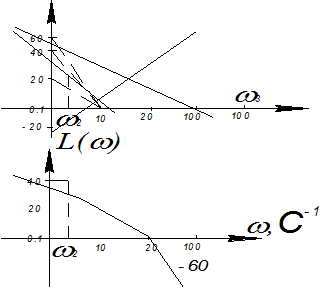
φ(ω)=-π/2-arctg(1.4 ω)+arc tg(0.5ω)- arctg(0.07ω/(1-0.0025 ω2))-arctg(0.001ω).
Звенья САР.
23. Понятие о звене.
Систему рассматривают с физической точки зрения, как соединение элементов. Элементов, входящих в САР, достаточно много. При исследовании системы интересуются неи физическими свойствамиодержанием ее элементов, а прежде всего их ДУ элементов.
Число уравнений, которые описывают элементы, не так уж велико. Некоторые из уравненияй выбраны в качестве типовых. Так возникло понятие «звено»- как часть системы, описанное определенными типовым ДУ.

При делении модели системы на части-звенья может оказаться, что один элемент может описываться как одним звеном, так и или соединением нескольких звеньев. Не исключено, что однимо звеном можно представить и соединением нескольких элементов. Типовым ДУ соответствуют типовые звенья.
Типовые звенья:
Однозначных установок для обьявления звена типовым не существует. Одним из примеров может служить следующий перечень звеньев, взятых в качестве типовых:
1) Усилительное звено..
2) Апериодическое звено 1-го порядка.
3) Апериодическое звено 2-го порядка.
4) Колебательное звено.
5) Консервативное звено.
6) Идеальное дифференциальнорующеее звено.
7) Идеальное интегрирующее звено.
8) Звено запаздывания.
9) Неустойчивое звено 1-го порядка.
Рассмотрим подробно все характеристики этих звеньев.
24. Усилительное звено
.
Уравнение звена y(t)=kv(t), k- коэффициент усиления звена. Передаточная функция W(s)=k, wv(t)=L-1{W(s)}=k∙δ(t) – ИПХ
W(S)=k
ω(t)=L-1{W(S)}=k∙δ(t) – ИПХ
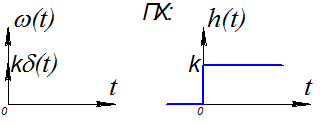 W(s)=k
W(s)=k
h(t)=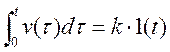
Графики импульсной переходной и переходной характеристик показаны на рис.
АФХ: W(jω)=k; вещественная частотная характеристика U(ω)=k; мнимая частотная характеристика V(ω)=0. Логарифмические частотные характеристики показаны на рис.
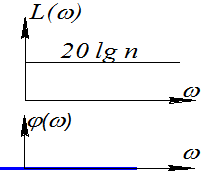
25. Апериодическое звено 1-го порядка
.
Ty/+y(t)=kV(t); k- коэффициент усиления
Т- постоянная времени. (Т>0)
Характеристическое уравнение имеет 1 корень:
TsS+1=0; sS1=-1/T<0
ПФ: W(sS)=
ИПХ: W(t)= L-1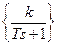 =ke-t/T
=ke-t/T
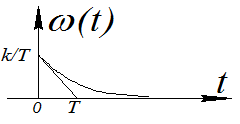
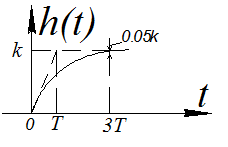
ПХ: h(t)=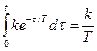 (1-e-t/T)
(1-e-t/T)
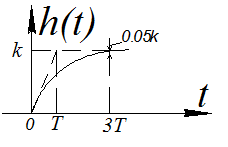
АФХ:
W(jω)=
U(ω) V(ω)
W(jω)=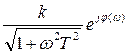
φ(ω)=- arctg(ωT)
На комплексной плоскости АФХ имеет вид, показанный на рис.
 ЛЧХ звена имеют вид
ЛЧХ звена имеют вид
L(ω)=20lgk - 20lg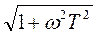
φ(ω)= -arctg(ωT)

26. Апериодическое звено 2-го порядка
Звено соответствует ДУ 2-го порядка.
T2y//+2ξTy/+y(t)=kV(t);
к- коэффициент усиления,.
Т- постоянная времени,.
ξ≥1 ξ- коэффициент колебанийтельности, ξ≥1.
.Характеристический многочлен допускает представление произведением 2-х сомножителей, т.е.
Т2sS2+2 ξTsS+1=(1+T1sS)(1+T2sS)
T1T2=T2; T1+ T2=2ξT; T1>T2 (ξ=1, T1=T2)
ПФ: W(sS)= 
ИПХ: W(t)=L-1 =
=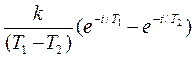
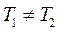
График переходной характеристики показан на рис.
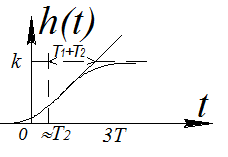
АФХ: W(jω)= 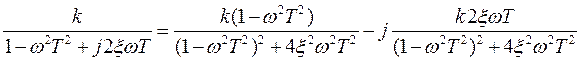
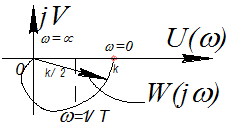
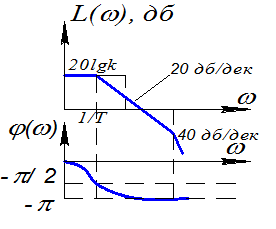
ЛЧХ звена определяются выражениями
L(ω)=20lgk - 20lg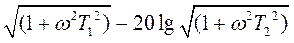 20lg
20lg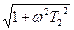
φ(ω φ(ω)= -arctg(ωT1) -arctg(ωT2)
27. Колебательное звено
ДУ звена.
T2y//+2ξTy/+y(t)=kX(t); 0<ξ<1
Характеристическое уравнение
T2sS2+2ξTsS+1=0
Имеет комплексно- сопряженные корни
; sS1,2=ω0(-ξ±j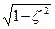 ),
),
где
ω0=1/T- собственная частота колебаний.
W(sS)= 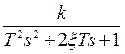 -ПФ звена,
-ПФ звена,
ИПХ: wω(t)=L-1{W(tыS)}= 
ωд=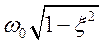 - демпфированная частота демпфированных колебаний, дискретизации.
- демпфированная частота демпфированных колебаний, дискретизации.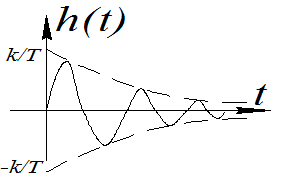
Tд=2π/ωд
-период демпфированных колебаний.
Переходная характеристика
h(t)=L-1{W(sS)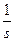 }=k(1-
}=k(1-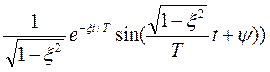
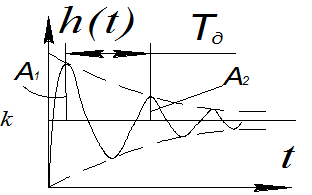
 φ=arctg
φ=arctg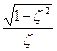 А1/A2=f(ξ) При ξ= 0.707 получается ПХ наилучшего вида, называемым техническим оптимумом.
А1/A2=f(ξ) При ξ= 0.707 получается ПХ наилучшего вида, называемым техническим оптимумом.
W(jω)= 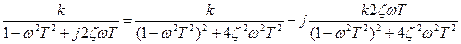
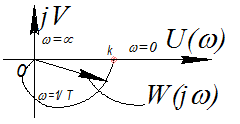
L(ω)=20lgk-20lg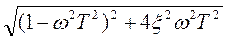

А1/А2=f(ξ)
ξ=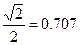
28. Консервативное звено.
 T2y//+y(t)=kV(t) ξ=0
T2y//+y(t)=kV(t) ξ=0
Характеристическое уравнение
ξ=0
T2sS2+1=0
; имеет чисто мнимые корни sS1,2=±j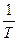
ПФ
W(sS)=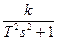
ИПХ
: wω(t)=L-1{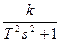 }=
}=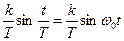
ω0=1/T
T0=2π/ ω0 ω=2 πT- период колебаний.
ПХ: h(t)=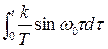 =k(1-cosω0t)
=k(1-cosω0t)

Частотные характеристики:
АФХ: W(jω)=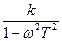
U(ω)= 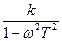 ; V(ω)=0
; V(ω)=0
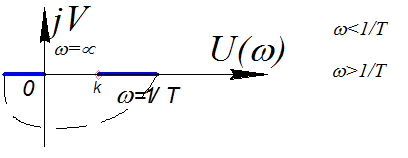
ЛЧХ: L(ω)=20lgk-20lg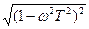
φ(ω)=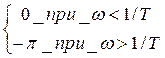
 Uy=
Uy=
T2=LC
29. Идеальное дифференцирующееиальное звено.
T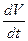 =y(t)
=y(t)
W(sS)=Ts
Звено является физически нереализуемым. Физически реализуют ПФS
W(sS)=
-cчитаемую как реальное дифференциальное звено.
T2<<T1
wω(t)=L-1{TsS}=TL-2{sS∙1}=T;wS//(t)=T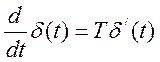
δ (t)=
(t)=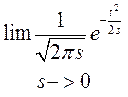 - гГаусовская кривая
- гГаусовская кривая
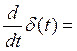
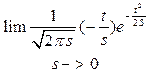
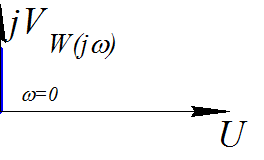 h(t)=T
h(t)=T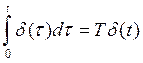
W(jω)=jωT
-совпадает с положительным направлением мнимой оси.
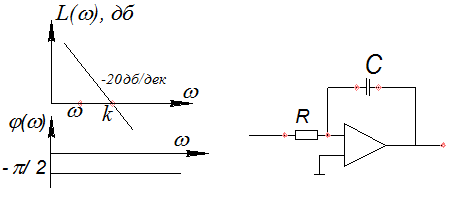
L(ω)=20lg ωT; φ(ω)=π/2
-ЛЧХ звена. Их графики показаны на следующем рис.
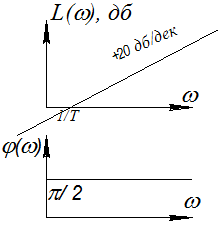
30. Идеальное интегрирующее звено.
Уравнения интегрирующего звена винтегральной
а) y(t)=ku
и б) Ty/=V(t)
- дифференциальной формах. Характеристическое уравнение
TsS=0 имеет корень; sS=0. ПФ
W(sS)=Ku/sS; ku=1/T; [ku]=C-1,
φ(ω)=-π/2
Из уравнений звена следует, что размерности входа и выхода звена одинаковы,т.е.

[V]=[y]; k=ku
wω(t)=kL-1{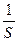 ∙1}=k 1(t)
∙1}=k 1(t)
h(t)=
W(j ω)=k/(j ω)=-jk/ ω
L(ω)=20lgk-20lg ω
φ(ω)=-π/2
31. Звено запаздывания
я.
Уравнение звена
y(t)=V(t-τ0); τ0- время запаздывания
1. vV(t)=δ(t); y(t)=wω(t)= δ(t-τ0)
 2. h(t)=
2. h(t)= 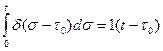
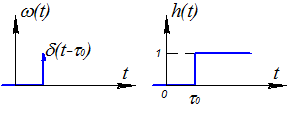
3. W(sS)=L-1{δ(t-τ0)}= 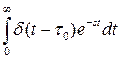 =
= =e-sδτo
=e-sδτo
W(sS)= e-sδτo- трансцендентная ПФ. Для преобразования её к дробно- рациональному виду используют конечные отрезки
Ее Разложение в рядразложений в ряд Паде.
 4. АФХ W(jω)=
4. АФХ W(jω)= 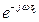 =cosωτ0=cos ωτ0-jsin(ωτ0).
=cosωτ0=cos ωτ0-jsin(ωτ0).
R(ω)=1; φ(ω)=- ωτ0.

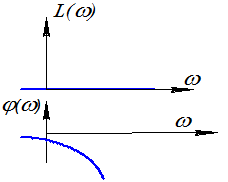
L(ω)=20lgl=0; φ(ω)=- ωτ0

32. Неустойчивое звено 1-го порядка.
Уравнение звена
Ty/(t)--y(t)=kvV(t). (Ty/-y=kV)
Харктеристическое уравнение TsS-1=0 имеет корень; sS1=1/T; T>0. Соответственно
W(sS)=k/(TsS-1)-ПФ и ИПХ
 wω(t)=L-1{ k/(TsS-1)}=
wω(t)=L-1{ k/(TsS-1)}= 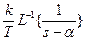 =(k/T)eαt
=(k/T)eαt
α=1/T>0 Это звено неустойчивое.
 Ty/-y=0
Ty/-y=0
Решение этого однородного ДУ
yсв(t)=y0eαt=> ∞; при t-->∞, если y0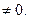
y0≠0 => ∞; t-->∞
hL(t)=k(eαt-1) 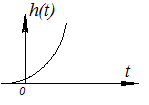
 W(jω)=k/(j ωT-1)=-k/(1+ ω2T2)-j
W(jω)=k/(j ωT-1)=-k/(1+ ω2T2)-j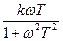
φ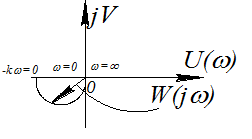 (ω)€[-π;- π/2] –звено является неминимально-фазовым.
(ω)€[-π;- π/2] –звено является неминимально-фазовым.
0< ω<∞
АЧХ звена
R(ω)= 
совпадает с неминимально-е фазовоеовым апериодическим звеном.
Для min фазовых систем все корни, определенные сомножителями ПФ, имеют отрицательные вещественные части. Для min фазовой системы вид одной частотной характеристики определяет вид другой.
U(ω)óV(ω) Они связаны между собой преобразованием Гильберта.
L(ω)óφ(ω)
ЛАЧХ совпадает с ЛАЧХ апериодического звена.
φ(ω)=-π+arctg ωT
Анализ систем.
33. Анализ устойчивости.
В основе анализа устойчивости лежат интуитивные предпосылки устойчивости, которые переложены на математику.
Интуитивно определяют устойчивость положения равновесия определяют:путем анализа свободного движения системы, возникающего после отклонения системы из точки А равновесия в точкуВ. Следующие графики поясняют эти определения.
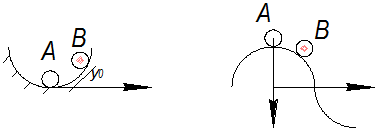

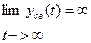
Уст. положение y(t)≡0 Неуст. положение y(t)≡0


y(t)≡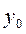 . Положение равновесия 0 уст. нейтральноа.
. Положение равновесия 0 уст. нейтральноа.
В САУ интуитивных определений устойчивости недостаточно. Для этой цели приходится использовать более строгие математические понятия. Рассмотрим их подробнее. Предположим, что система описана ДУ
z/=G(z,U) (1) z= , z€Rn G=
, z€Rn G= ,G€Rn; U€Rm
,G€Rn; U€Rm
m
G= , G€Rn; U€Rm
, G€Rn; U€Rm
U=U(t)- известная векторная функция времени. Поэтому ДУ (1) можно рассматривать в виде
z/=G1(z,t) (2)
Предположим, что уравнение (2) имеет решение r(t), t€[0;∞] устойчивость которого надо исследовать.Его рассматривают как - невозмущенное решение при. r(0)=r0.
Требуется определить устойчивость этого решения или, другими словами, невозмущенного движенияе устойчивости этой системы. Для определения устойчивости невозмущенного решения требуется исследование всех других решений системы (2), которые получаются при начальных условиях z0, не равных начальным условиям, при которых получено невозмущенное решение. То-есть.
z(t), при z0=z(t0)≠r0
Исследование всех решений системы (2) представляет собой концептуальную проблему, т. к. нелинейные ДУ не имеют общих методов решения. Поэтому применяются различные приемы, которые позволяют косвенно оценить эти решения.
1. Второй или прямой метод А. М. Ляпунова.
2. Линеаризованные уравнения- 1-ый метод А. М. Ляпунова.
34. Исследование устойчивости линеаризованных систем
Основные положения прямого метода Ляпунова:
Обозначим общее решение уравнения (2) в виде z(t)=r(t)+x(t).
x(t)- отклонение возмущенного решения z(t) от невозмущенного r(t).
Отклонения x(t) удобно представлять в виде приведенного уравнения.
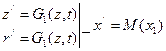 (3)- приведенное уравнение системы.
(3)- приведенное уравнение системы.
M=G(r+x1t)-G1(r1t)
M(0)=0
x(t)≡0- это решение соответствует положению авновесия в начале координатной системы.
Если приведенная система находится в начале координат, то исходная система совершает невозмущенное движение. Если положение равновесия в начале координат будет удовлетворять условиям устойчивости, то будет устойчивым и невозмущенное решение системы (2). Для положения равновесия в начале координат или для тривиального решения системы (3) Ляпуновым даны 3 определения:
1. нормы вектора
||x||
lp=||x||p, p=1,2,3…
||x||p=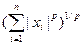
||x||2= - длина вектора.
- длина вектора.
x(t)≡0
Тривиальное решение называется устойчивым, если для любого ε>0 найдется такая величина δ= δ(ε)>0, что ||x0||< δ, ||x(t)||< ε, t€[0,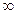 ).
).
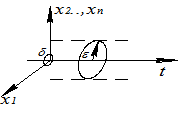
Все решения, начинаясь в δ- области, не выходят за пределы δ-трубки.
2. Если тривиальное решение:
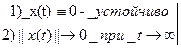 асимптотическая устойчивость
асимптотическая устойчивость
Если при асимптотической устойчивости величина δ не ограничена, то систему называют асимптотически устойчивой в целом.
3. Если для любого ε>0 найдется величина δ и хотя бы одно решение x(t)- для которого существует момент t=t1, при котором ||x(t1)||=ε, то тривиальное решение системы (3) неустойчиво.
x/=H(x) (3)
Пусть H(x) можно представить в виде разложения.
H(x)=Ax+R(x) (4)
A=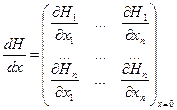 - матрица Якоби
- матрица Якоби
R(x)€Rn- остаточный член разложения.
||R(x)||≤||x||1+α; α>0,
Тто остаточным членом можно пренебречь и вместо уравнения (3) рассмотреть линеаризированное уравнение.
x/=Ax (5) - уравнение первого приближения.
Общее решение уравнения (5): x(t)=eAtx0
Следующие 3 уравнениятеоремы Ляпунова позволяют связать устойчивость тривиального решения исходного (3) и приведенного (5) уравненияй.
det(sδI-A)=0, sSi, i=1…n, I=diag1.
Матричный экспоненциал определяется корнями характеристического уравнения sSi=sSi(A)- собственныео значенияе (числа матрицы А)
1. Теорема (об устойчивости).
Si, i=1…n, Re(Si=Si(A))<0, i=1…n
Тривиальное решение системы (5) асимптотически устойчиво в целом, а тривиальное решение системы (3) будет асимптотически устойчивым при малых отклонениях.
2. Теорема 2 (о неустойчивости)
Если среди корней характеристического уравнения Si найдется хотя бы один Sk такой, что Resk>0, то тривиальное решение системы (3) и cистемы (5) неустойчиво.
3. Теорема 3 (критический случай)
Если у характеристического уравнения все корни левые, за исключением одного нулевого или пары чисто мнимых корней, то тривиальное решение системы (5) устойчиво, не асимптотически, а об устойчивости решения системы (3) в этом случае судить нельзя, т. к. устойчивость зависит от членов, отбрасываемых при линеаризации.
sSi=Ssi(A), Resi<0, i=1:n –условие теоремы 1; Res sk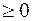 , k
, k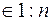 - теорема 2;
- теорема 2;
sSl=0; sSk,k+1=±jβk,-условия теоремы 3.
При исследовании систем, в первую очередь, надо над обеспечениемть условия их ассимптотичнеской устойчивости. Это, т. е. все корни должны являеться необходимым условием работоспособности систем. Неустойчивые системы неуправляемые.
Определение устойчивости по местоположению корней характеристического уравнения
det(sSI-A)=a0sSn+a1sSn-1+…+an=0
на комплексной плоскости, вычисленных численно, Нахождение корней Si, i=1…nможет привести к дает в весьма существенные погрешностями хода.
Корни с нулевой вещественной частью, расположенные на мнимой оси, за счет погрешностей вычислений, могут получить вещественную часть, либо положительную, либо отрицательную, или наоборот..
35. Критерии устойчивости.
Критериями устойчивости называют правила, позволяющие оценивать местоположение корней характеристического уравнения без их непосредственного вычисления. Для оценки местоположения эти критерии используют различные характеристики систем, тесно связанные с ее характеристическими уравненияеми.
Критерии:
1) аАлгебраические;
2) частотные.
Исходя из модели системы эти критерии можно интерпретировать следующим образом:

Пусть W(sS)=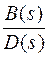
B(sS)=b0sSm+ b1sSm-1+… +bm;
D(sS)=d0sSn+ d1sSn-1+… +dn.
Уравнение D(sS)=0- характеристическое уравнение разомкнутой системы.
Для исследования устойчивости используют корни характеристического уравненияй замкнутой системы. Характеристическое уравнение замкнутой системы:
Д(sS)=D(sS)+B(sS)=0 является знаменателем ПФ
Ф(sS)= 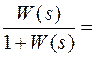
 .
.
Д(sS)=a0sSn+ a1sSn-1+…+an
Алгебраические критерии устойчивости:
1) Критерий Рауса.
2) Критерий Гурвица.
3) Критерий Льюенара-Шипара.
Частотные критерии:
1) Критерий Михайлова
Д(jω)=Д(sS), s=S(jω, 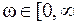 ] –годограф характеристического многочлена.)
] –годограф характеристического многочлена.)
2) Критерий Найквиста
W(jω)=W(sS), sS= jω, 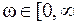 ] –АФХ разомкнутой системы и условия её устойчивости..
] –АФХ разомкнутой системы и условия её устойчивости..
3) Логарифмический критерий устойчивости. Это критерий Найквиста, но вместо АФХ используются ЛЧХ.
1. Критерий Гурвица:

W(sS)= 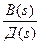
B(sS)=
Д(S)=D(S)+B(S)=a0Sn+ a1Sn-1+…+an
Формирование матрицы Гурвица.
Гr=
1. ai>0, i=1…n
2. Рассмотрим диагональные миноры
Δi, i=1…n Δn=an Δn-2
Δi>0; Δi- определители Гурвица.
Пусть n=3, тогда характеристическое уравнение:
Д(S)=а0S3+ а1S2+ а2S+ а3
Г=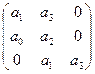
Условие устойчивости:
Δi=a1>0
Δ2=a1a2-a0a3>0
Δ3=a3∙ Δ2
ai>0, i=0…n
При n=4:
Г=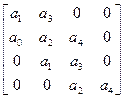
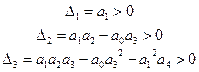
Если изменять параметры системы так, чтобы она из устойчивой превратилась в неустойчивую, то при таком изменении первым обращается в 0 Δn-1:
Δi>0; Δn-1=0; Δn-1<0
Критерий Льенара-Шипара:
n- четное- проверяются все нечетные определители Δ2i-1: i=1…n/2
n- нечетное- проверяются все четные определители Δ2i: i=1…(2n-1)/2
Определение критического коэффициента усиления разомкнутой системы:
Δi>0; i=1…n-2
Δn-1=0 при k=kкр
Все определители до n-2 должны быть положительными, а Δn-1=0.
Все эти определители должны давать 2 типа неравенств:
а) k>kкр, Δn-1<0- система неустойчива
k<kкр, Δn-1>0- система устойчива
б) kкр1 <k<kкр2, Δn-1>0- система устойчива
k (kкр1, kкр2), Δn-1<0- система неустойчива.
(kкр1, kкр2), Δn-1<0- система неустойчива.
Пример:
Пусть разомкнутая система имеет вид:
W(S)= 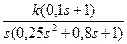
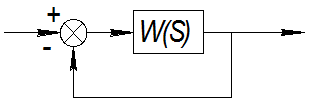
Определим для нее возможные значения kкр, используя исследования устойчивости, вытекающие из критерия Гурвица. Характеристический многочлен замкнутой системы:
Д(S)=0.25S3+0.8S2+(1+0.1k)S+k=0
Г= Δ1=0.8>0
Δ1=0.8>0
Δ2=0.8(1+0.1k)-0.25k=0
kкр=0.8/0.17≈5
k>kкр- неустойчивое; k<kкр- устойчивое.
ПФ разомкнутой системы включает в себя звенья запаздывания. В этом случае характеристическое уравнение будет иметь не конечное, а бесконечное число корней. Чтобы ограничиться конечным числом корней надо использовать разложение eSro в ряд Падэ, либо использовать критерии, которые не критичны к числу корней характеристического уравнения. Одним из таких критериев является критерий Найквиста.
2. Критерий Найквиста.
Он используется для анализа устойчивости систем с единичной ОС, основываясь:
а) на устойчивости разомкнутой системы
б) на виде АФХ W(jω) разомкнутой системы
ПФ замкнутой системы: Ф(S)= 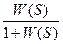
АФХ замкнутой системы: Ф(jω)= 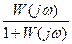
Устойчивость будет определяться нулями функции: 1+W(S)
Пусть W(S)= 
D(S)=d0Sn+d1Sn-1+…+dn=d0(S-S1)…(S-Sn)- характерный многочлен разомкнутой системы.
Характерный многочлен замкнутой системы:
Д(S)=D(S)+B(S)=a0 (S-S1)…(S-Sn)=a0Sn+ a1Sn-1+…+an
Для анализа устойчивости замкнутой системы рассматривают угол поворота вектора или вспомогательной функции f(jω)=1+W(jω) при ω [0;∞)
[0;∞)
Угол поворота можно описать как Δargf(jω), ω [0,∞)
[0,∞)
Так как f(jω) есть отношение векторов, то ее можно представить:
f(jω)= 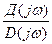
Δargf(jω)= ΔargД(jω)- ΔargD(jω)
ω [0,∞); ω
[0,∞); ω [0,∞) ω
[0,∞) ω [0,∞)
[0,∞)
1 Случай, когда в характеристическом уравнении разомкнута система:
D(S)=d0(S-λ1)…(S- λn)=0
q- корней λi имеет положительные вещественные части Re λi>0.
(n-q) корней λi имеют отрицательные вещественные части Re λi<0, а в характеристическом уравнении замкнутой системы:
Д(S)=a0 (S-S1)…(S-Sn) все n корней части Si, I=1…n имеют отрицательные вещественные части ReSi<0.
Условие устойчивости этой системы в замкнутом состоянии:
Δargf(jω)= n -[(n-q)
-[(n-q) +q(-
+q(- )]=qπ=
)]=qπ=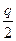 2π
2π
Если q=0, то система устойчива, если Δargf(jω)=0
ω [0;∞)
[0;∞)
Условие будет выполнено, если годограф f(jω) не охватывает начало координат (граф. 1).
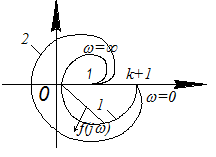
Если годограф охватывает начало координат, то угол оборота не равен 0 и система неустойчива (граф. 2).
От плоскости f(jω) можно перейти к плоскости W(jω), если сместить начало координат на 1. Точка о переходит в точку (-1;j0).
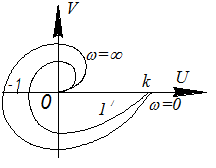
Точка с координатами (-1,j0) называется критической.
Если система устойчива в разомкнутом состоянии q=0 и ее АФХ не охватывает критическую точку, то система в замкнутом состоянии устойчива. Если же охватывает критическую точку, то система в замкнутом состоянии неустойчива. (кривая 2/).
Таким способом можно определить замкнутую систему для статической системы- когда ν=0.
В общем случае ν=0,1,2,3 и для этих случаев АФХ начинается в бесконечность ν=1: “-j∞”; ν=2: “-∞”; ν=3: “j∞”
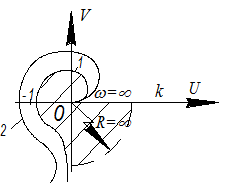
Для анализа устойчивости надо исследовать АФХ при малых изменениях ω [-0;0+]. В этом случае Δarg=-νπ/2
[-0;0+]. В этом случае Δarg=-νπ/2
ω [-0;0+]
[-0;0+]
Система 1 не охватывает 1, j0, она устойчива. Система 2 охватывает критическую точку, она неустойчива.
Для ν=2
 Система 1 устойчива
Система 1 устойчива
Система 2- неустойчива
ν=3
Система 1 в замкнутом состоянии устойчива.
Система 2- неустойчива.
Если разомкнуть систему устройства и ее АФХ огибает критическую точку (-1;j0) снизу, то в замкнутом состоянии система устойчива. Если это условие нарушено- АФХ огибает критическую точку сверху, то в замкнутом состоянии система неустойчива.
2) q>0, система не минимально фазовая. В этом в случае надо использовать любое условие, подтверждающее, что Δargf(jω)=qπ
ω [0;∞)
[0;∞)
Преимуществом критерия Найквиста является то, что в окончательной формулировке фигурирует лишь устойчивость разомкнутой системы и вид АФХ, т. е. устойчивость систем можно определить по экспериментально снятой АФХ разомкнутой системы безо всякой кК аппроксимации. Это позволяет анализировать устойчивость системы, содержащей звенья запаздывания.
Другим достоинством является то, что он позволяет ввести меру устойчивости. Мера устойчивости выступает, в этом случае, как запасы устойчивости.
36. Запасы устойчивости
Запасы устойчивости x-ют степень удаления АФХ от критической точки при огибании ее снизу и выступают в виде:
1) запас по модулю (амплитуде)
2) запас по фазе.
Эти понятия вытекают из условия существования незатухающих колебаний в системе с ОС.
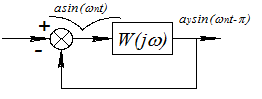 Пусть на входе разомкнутой системы в виде рассогласования возникает сигнал asinωПt. На выходе сигнал aуsin(ωПt-π). По цепи ОС он инвертируется и становится asin(ωПt-2π). Если аy=W(jωП)-а=а, то амплитуда будет оставаться неизменной, получим генератор гармонических колебаний. Условие:
Пусть на входе разомкнутой системы в виде рассогласования возникает сигнал asinωПt. На выходе сигнал aуsin(ωПt-π). По цепи ОС он инвертируется и становится asin(ωПt-2π). Если аy=W(jωП)-а=а, то амплитуда будет оставаться неизменной, получим генератор гармонических колебаний. Условие:

В системе, в которой выполняется баланс амплитуд и фаз, АФХ проходит через критическую точку. В этом случае в характеристическом уравнении имеется пара чисто мнимых корней.
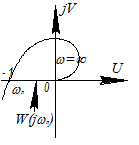
Система, имеющая определенный запас устойчивости должна иметь АФХ следующего вида:
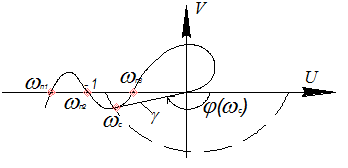
1) Для определения запаса устойчивости по фазе проводится окружность единичного радиуса с центом в начале координат. В точке пересечения этой окружности с АФХ частота равна частоте среза:
ω= ωс R(ωc)=|W(jωc)|=1
φ(ωс) будет определяться углом.
Угол γ=π+φ(ωс)>0 называется запасом устойчивости по фазе.
2) Запас по модулю определяется исходя из точек АФХ с частотами ωπ2 и ωπ3, ближайшие к критическим. Эти точки являются решением уравнения φ(ω)=-π; ωπ1; ωπ2; ωπ3.
W(jwП2)=-H; H>1
W(jwП3)=-h; h<1
Запас устойчивости по модулю (амплитуде) будет определяться min-ой из точек
min(H;1/h)
Чем ближе эти величины к 1, тем меньше запас устойчивости.
Пример:
W(S)=k/S (1) g=900 óp/2
W(S)=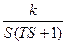 (2)
(2)

37. Анализ влияния коэффициента усиления разомкнутой системы на устойчивость замкнутой системы.
1) W(S)=k·W0(jω)
ν=0
W0(j0)=1
При увеличении коэффициента усиления система может из устойчивой превратиться в неустойчивую. Это произойдет при k>kкр.
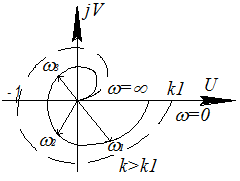
Такая АФХ называется АФХ I рода.
k<kкр R(ωП; kкр)=1
система устойчива φ(ωП)=-π
k>kкр- система неустойчива.
2) АФХ II рода

При увеличении k ωπi+1 →-1, j0
При уменьшении k ωπi→-1, j0
Для такой системы может быть несколько kкр. Условие устойчивости kкрi< k< kкрi+1 - система устойчивая.
3) При любом k охватывают точку системы, которые неустойчивы при любом k>0 называется структурно-неустойчивыми.
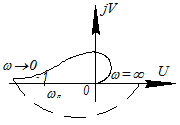
Для этих систем φ(ω)<-π
ω [0;∞)
[0;∞)
Без введения корректирующих устройств обеспечить устойчивость таких систем нельзя. После коррекции структурно неустойчивой система становится обычной системой. В обычных системах увеличение коэффициента усиления приводит к увеличению запаса устойчивости.
38. Логарифмический критерий устойчивости
Является видоизмененным критерием Найквиста, когда вместо АФХ разомкнутой системы используется ЛЧХ этой системы. Условие устойчивости вытекает из аналогии между АФХ и ЛЧХ.
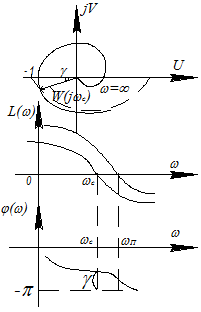
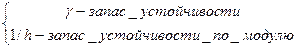
R(ωC)=1 ó L(ωC)=0
Для рассматриваемой характеристики ωC< ωπ; R(ωπ)=h<1 L(ωπ)<0
Запас устойчивости по фазе будет дополнением φ(ωС) до уровня π. Запас устойчивости по амплитуде ΔL=/L(ωπ).
Если изменять коэффициент усиления, то L(ω) будет поступательно подниматься при увеличении k и опускаться при его уменьшении.
k= kкр, когда ωС= ωП- граница устойчивости.
Таким образом, условие устойчивости: ωС< ωП
γ, ΔL- запасы устойчивости.
ωС=ωП- граница устойчивости: γ=0; ΔL=0
ωС>ωП- условие неустойчивости.
Рассматриваемые критерии устойчивости предполагают, что определение характеристик систем не вызовет дополнительных вычислений, что характерно для моделей вх-вых.
Несколько иная ситуация возникает, если для описания системы используется уравнение состояния.
39. Определение устойчивости при описании систем в пространстве состояний.
Предположим, что имеется замкнутая система, которая будет определяться выражением:
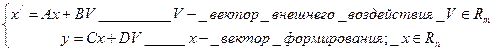
Матрицы А, В, С,D- матрицы соответствующих размеров y Rl. Если использовать критерии Гурвица, то ею непосредственное использование будет связано со следующим вычислением:
Rl. Если использовать критерии Гурвица, то ею непосредственное использование будет связано со следующим вычислением:
1) Нахождение корней характеристического уравнения
det(SI-A)=0 через коэффициент матрицы А.
a0Sn+a1Sn-1+…+an=0
Вычисление определителя сопрягается, значит погрешность, а корни уравнения степени n>10. Чрезвычайно чувствительны к изменению коэффициентов.
2) Условие устойчивости Δi>0, i=1…n-1 не дает однозначного ответа при приближенных вычислениях. Если же анализировать устойчивость по корним характеристического уравнения, то необходимо вычислить det(SI-A)=0 и найти коэффициенты ai