Un называется общим членом ряда

Ряд считается заданным,если известен общий член u_n,выраженный как функция

его номера n: u_n = f(n). Возможно существование ряда,в котором все элементы равны.

Ряд может иметь конечное или бесконечное количество членов.

ПРИМЕРЫ:

Общий элемент a_n:Первые элементы: Десятый элемент:

1). a_n= 1/n 1+1/2+1/3+1/4+… 1/10

2). a_n= 1/2ⁿ ½+1/4+1/8+1/16... 1/1024

3). a_n=(-1)ⁿ 2n -2,4,-6,8... 20

4). a_n=1/n! 1/1!+1/2!+1/3!+1/4!+... 1/10!

5). 2+17-3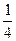+196+… нельзя считать заданным (нет формулы аn)

6). 2+5+8+… общий член ряда задается формулой аn=3n-1(А.П.)

Иногда элементы ряда определяются по формуле,в которой имеется связь

последующего элемента с элементом предыдущим.

ПРИМЕР. Дано u₁=1, u₂=1/2,найти элементы ряда,если общий элемент имеет вид:

u_n=(1/2)u_n-1 + (1/3)u_n-2.

Найдем u₃=(1/2)u₂ + (1/3)u₁=(1/2)(1/2) + (1/3)*1=7/12_.

u₄=(1/2)u₃ + (1/3)u₂=(1/2)(7/12) + (1/3)*(1/2)=11/24...

получим ряд 1+1/2+7/12+11/24+...

Арифметическая прогрессия имеет вид:

a₁+(a₁+r)+(a₁+2r)+(a₁+3r)+...[a₁+(n-1)r] +... или 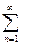∑ [a₁+r(n-1)],

где a₁≠0, a₁ – первый элемент прогрессии арифметической, r - разность.

ПРИМЕР. Общий элемент ряда: a_n=a₁+(n-1)r

2 + 5 + 8 + 11 + 14 +... [ a₁+(n-1)r] +...

Это арифметическая прогрессия с a₁=2 и разностью r=3.

Прогрессия геометрическая или геометрический ряд имеет вид:

u₁ + u₁q + u₁q² + u₁q³…+ u₁q^n-1+… или 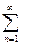u₁q^n-1,

где u₁≠0, u₁ – первый член геометрической прогрессии, q - знаменатель.

ПРИМЕР. Найти ряд с общим элементом (-1)^n-1:

1 – 1 + 1 – 1 + 1 - 1+... (-1)^n-1+... или 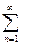(-1)^n-1

Имеем геометрический ряд с a₀=1 и знаменателем q=-1.

Гармоническим рядом называется ряд с u_n = 1/n: 1+1/2+1/3+1/4+...1/n+... или ∑1/n.

Обобщенный гармонический ряд : 1+1/2^α+1/3 ^α+1/4 ^α+...1/n ^α+... или ∑1/n ^α,

где α -заданное число.

Определение. Сумма первых n элементов ряда называется частичной суммой ряда и обозначается S_n: S_n=u₁+u₂+u₃+…+u_n

Рассмотрим частичные суммы:

S₁= u₁

S₂= u₁+u₂

S₃ = u₁+u₂+u₃

.........................

S_n = u₁+u₂+u₃ +…+u_n

Определение. Числовой ряд u₁+u₂+u₃+…+u_n +…= 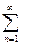u_n называется сходящимся,

если его частичная сумма S_n = u₁+u₂+u₃ +…+u_n uмеет предел при n→∞.

Величина S=S_n называется при этом суммой ряда,а число

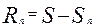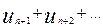= - остатком ряда.

Или: Ряд 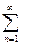u_n называется сходящимся, если существует конечный предел S=S_n последовательности частичных сумм ряда, этот пределназывается суммой ряда и записывается S= 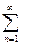u_n .

Определение. Если S_n не существует или S_n =∞, то ряд называется расходящимся и суммы не имеет.

ПРИМЕРЫ. 1). 1+1+1+…, расходится, S_n =n→∞ при n→∞. (u₁=u₂=…=u_n=1);

2). 0+0+0+…, сходится, S_n =0, (u₁=u₂=…=u_n=0);

3). 1-1+1-1+1… расходится,так как последовательность частичных сумм

S₁=1, S₂ =0, S₃=1,_… не имеет предела;

4). 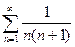сходится,

Действительно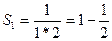

……………………………………………….

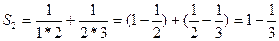
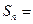
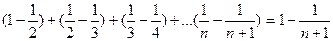
Следовательно, 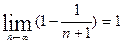, т.е. ряд сходится,его сумма равна 1.

5). Рассмотрим ряд a+aq+aq²+…+aq^n-1+…

Это прогрессия геометрическая с первым элементом 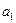= а и знаменателем q (a≠0).

Сумма n первых элементов прогрессии геометрической (если q≠1),равна 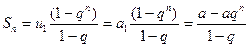или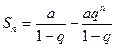

1). Если IqI<1, qⁿ→∞ при n→∞ и поэтому,

_{S n=} ()=

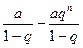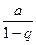
Итак, если q<1 ряд сходится и сумма S= .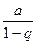

2). Если q>1, IqI→∞,при n→∞ e 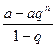→ ±∞, при n→∞

следовательно S_n не существует.

Итак, если q>1 ряд расходится.

3 ). Если q=1, ряд имеет вид: a+a+a+…

Поэтому S_n=na, S_n=∞, ряд расходится.

4). Если q= -1, ряд записывается: a-a+a-a+… и

S_n= ,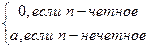

S_n не имеет предела, ряд расходится.

Следовательно, геометрический ряд 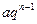(a₁≠0) сходится, если IqI<1,

Дата добавления: 2014-01-15