Метод подстановки

.

И.

Относительно осей Ох,Оу вычисляются по формулам

Моменты инерции плоской фигуры. Моменты инерции плоской фигуры

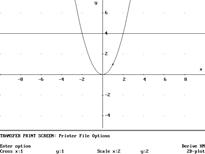
ПРИМЕР . Вычислить обьем тела,ограниченного поверхностями x=0, y=0, x+y+z=1, z=0.

Решение: _z

_y

x=0,y=0, x+y=1 ^x+y+z=1

Dx+y=1 D 1 х

y=0 1 x+y=1

^x=0x

у

Рис.7 Рис.8

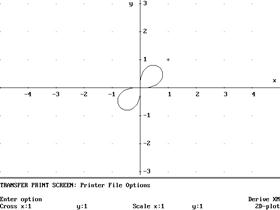
ПРИМЕР. Вычислить площадь фигуры Лемниската (x²+y²)²=2xy.

Используя полярные координаты

x=rcosθ, y=rsenθ, получим:

(r²cos²θ +r²sen²θ)²=2r²senθ cosθ,

Рис.9

r²=sen2θ, 0≤ r ≤ √ sen2θ, 0≤ θ ≤ π/4.

.

§2.Тройной интеграл.

Обобщением опроеделенного интеграла на случай функции трех

переменных является так называемый «тройной интеграл». Теория тройного

интеграла аналогична теории двойного интеграла.

Пусть в замкнутой области V пространства Оxyz задана непрерывная

функция u = f(x,y,z) Разбив область V сеткой поверхностей на n частей

Vi(i=1,..n) и выбрав в каждой из них произвольную точку Мi(х i,уi, zi) составим

интегральную сумму

∑ f (М _i ) ∆v_i (2.1)

для функции f(x,y,z) по области V ( здесь ∆v _i обьем элементарной области v_i.).

Если предел интегральной суммы существует при неограниченном увеличении числа

n таким образом,что каждая элементарная область v _i стягивается в точку(т.е. диаметр области di cтремится к нулю,т.е. di →0)то его называют тройным интегралом от функции u = f(x,y,z) по области V и обозначают

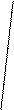
∫∫∫ f(х,у,z)dv или ∫∫∫ f(х,у,z)d xdydz

^VV

Итак,имеем 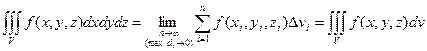, (2.2)

где dv= dxdydz – элемент обьема.

Тройной интеграл обладает теми же свойствами,что и двойной интеграл.

2.1.Вычисление тройного интеграла в декартовых

координатах.

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

Пусть областью интегрирования V является тело,ограниченное снизу поверхностью Z=Z1(x,y), сверху- поверхностью Z=Z2(x,y), при чем Z1(x,y) ≤ Z2(x,y)

и эти функции непрерывны в области D,являющейся проекцией тела на плоскость Оху.

Будем считать область V - правильной в направлении оси О z, любая прямая,

параллельная оси О z, пересекает границу области не более чем в двух точках.

(Рис1-неправильная, Рис.2-правильная).Тогда для любой непрерывной

в области f (x,y,z) имеет место формула

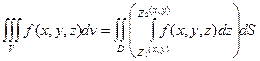
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного.

_{Z Z= Z2 (X,Y)}

^Z

_{Z= Z1 (X,Y)}

_{a Y}

_{X b D}

X

^Y _{у=φ1(X,Y) у=φ2(X,Y)}

Рис.1 Рис.2

Если область D ограничена линиями х=а, х=в(а<в), у= φ₁(x), y= φ₂(x),_,

где φ₁(x), φ₂(x) непрерывны на отрезке [а,в] при чем φ₁(x), _≤ φ₂(x), то переходя от

двойного интеграла к повторному,получаем формулу

,

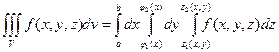по которой вычисляется тройной интеграл в декартовых координатах.

ПРИМЕР. Найти обьем тела,ограниченногоциллиндром y=x² и поверхностями

y+z=4 и z=0.

Решение:

Эта область V - правильная в направлении оси О Z

ограничена поверхностями z=4-y и z=0.

Проекцией на Oху есть область D – парабола

y=x² и прямая y=4.

Рис.3

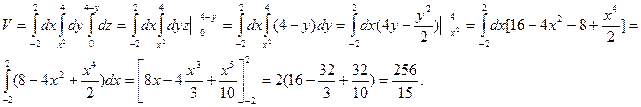
2.2.Замена переменных в тройном интеграле.

Вычисление тройного интеграла в цилиндрических и сферических координатах.

При вычислении тройного интеграла,как и двойного часто применяется

Пусть совершена подстановка x = φ (u,v,w), y = ψ(u,v,w), z=χ(u,v,w). Если

эти функции имеют в некоторой области V* пространства Оиvw непрерывные частные производные и отдичный от нуля определитель(якобиан) ,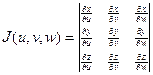

то справедлива формула замены переменных в тройном интеграле:

.

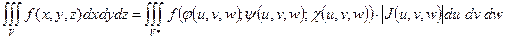Для вычисления тройного интеграла часто используются цилиндрические координаты.

Положение точки М(х,у,z) в пространстве Оxyz можно определить

заданием трех чисел r, θ, z (Рис.4),где

r - длина радиуса-вектора проекции точки М на плоскость О xy,

θ- угол,образованный этим радиусом-вектором с осью Ox,

z –аппликата точки М.

Эти три числа (ρ, θ, z) называются цилиндрическими координатами точки М.

Они связаны с декартовыми координатами следующими соотношениями:

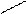x= r cosθ; y= r senθ; z= z, где r ≥0, 0≤θ≤2π; z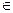R.

_z

М(θ,r,z)

_{z y}

^θ

r

^x

Рис.4

Вычислим якобиан: .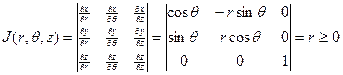

Формула замены переменных имеет вид:

.

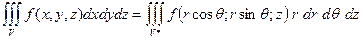Замечание. К цилиндрическим координатам удобно переходить,если область интегрирования образована цилиндрической поверхностью.

ПРИМЕР. Определить интеграл I = ∫∫∫ (y²+ z²) dxdydz,

^V

если областью интегрирования V является прямоугольный цилиндр,высотой 2h

и радиусом 1. Z

Выберем систему координат:

цилиндрическую,

используем формулы

x= r cosθ; y= r senθ; z= z,

поставим в интеграл 2h _y

I = ∫∫∫ (y²+ z²) dxdydz. ^R

^{V х}

В координатах циллиндрических: Рис.5

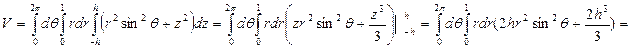
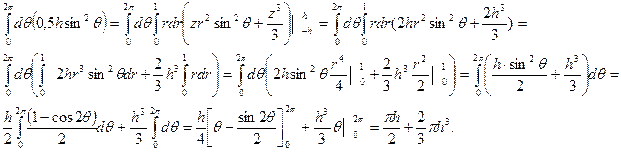
Дата добавления: 2014-01-15