
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Положительное направление- против часовой стрелки(налево)
|
|
|
|
Х
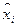
Рис.1.
Эту сумму называют интегральной суммой для функции f(х,у) по кривой АВ.
Определение. Пусть 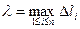 - наибольшая из дуг деления.Если при
- наибольшая из дуг деления.Если при 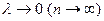 существует конечный предел интегральных сумм,то его называют криволинейным интегралом от функции f(х,у) по длине кривой АВ (или 1-го рода) и обозначают
существует конечный предел интегральных сумм,то его называют криволинейным интегралом от функции f(х,у) по длине кривой АВ (или 1-го рода) и обозначают 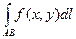 т.е.
т.е. 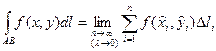 .
.
ТЕОРЕМА. Если функция f(х,у) непрерывнав каждой точке гладкой кривой(в каждой точке 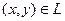 существует касательная к данной кривой и положение ее непрерывно меняется при перемещении точки по кривой),то криволинейный интеграл 1-го рода существует и его величина не зависит ни от способа разбиения кривой на части,ни от выбора точек в них.
существует касательная к данной кривой и положение ее непрерывно меняется при перемещении точки по кривой),то криволинейный интеграл 1-го рода существует и его величина не зависит ни от способа разбиения кривой на части,ни от выбора точек в них.
Основные свойства криволинейного интеграла 1-го рода.
1). 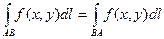 , т.е криволинейный интеграл 1-го рода не зависит от направления интегрирования.
, т.е криволинейный интеграл 1-го рода не зависит от направления интегрирования.
2). 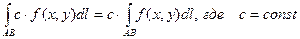 .
.
3). 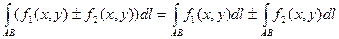 .
.
4). 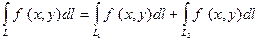 ,если путь интегрирования L разбит на части
,если путь интегрирования L разбит на части  такие,что
такие,что 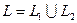 и
и 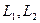 имеют единственную общую точку.
имеют единственную общую точку.
5).Если для точек кривой L выполнено неравенство 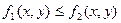 ,то
,то 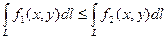 .
.
6). 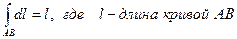 .
.
7). Теорема о среднем. Если функция f(х,у) непрерывна на кривой АВ,то на этой кривой найдется точка 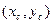 такая,что
такая,что 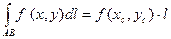 .
.
1.2. Вычисление криволинейного интеграла 1-го рода.
Явное представление кривой интегрирования.
Если кривая АВ задана уравнением 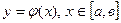 ,где
,где 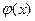 - непрерывно дифференцируемая функция,то
- непрерывно дифференцируемая функция,то 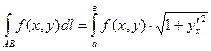 . (1.2)
. (1.2)
Подинтегральное выражение в правой части формулы получается заменой  и
и
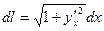 .
.
ПРИМЕР. Вычислить 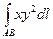 ,где АВ- отрезок прямой между точками О(0,0) и А(4,3).
,где АВ- отрезок прямой между точками О(0,0) и А(4,3).
Уравнение прямой ОА есть: 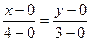 , 3х=4у или
, 3х=4у или 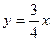 ,
, 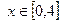 ,тогда
,тогда
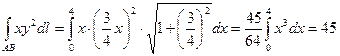 .
.
Параметрическое представление кривой интегрирования.
Если кривая АВ задана уравнениями 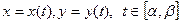 ,где
,где 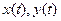 - непрерывно дифференцируемые функции параметра t,причем точке А соответствует
- непрерывно дифференцируемые функции параметра t,причем точке А соответствует 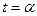 ,точке В- значение
,точке В- значение 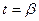 ,то
,то 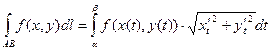 . (1.3)
. (1.3)
Полярное представление кривой интегрирования.
Если плоская кривая АВ задана уравнением 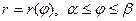 в полярных координатах,то
в полярных координатах,то 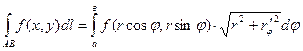 . (1.4)
. (1.4)
Подчеркнем,что нижний предел определенного интеграла в формулах (1.2)-(1.4) должен быть меньше верхнего.
1.3.Некоторые приложения криволинейного интеграла 1-го рода.
1). Длина кривой АВ плоской или пространственной линии вычисляется по формуле
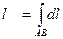 .
.
2 ). Масса материальной кривой AB (провод,цепь,трос,…) определяется по формуле
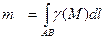 ,
,
где 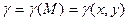 - плотность кривой в точке М.
- плотность кривой в точке М.
3). Статические моменты,центр тяжести.
Статические моменты относительно осей Ох,Оу и координаты центра тяжести материальной
кривой АВ: 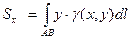 ,
, 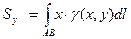 ;
;
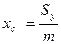 ,
, 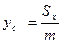 .
.
 4). Моменты инерции в отношении осей координат.
4). Моменты инерции в отношении осей координат.
Для материальной кривой АВ моменты инерции в отношении осей координат Ох,Оу
и начала координат 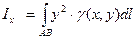 ,
, 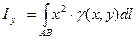 ,
, 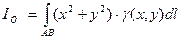
5). Площадь цилиндрической поверхности.
Если направляющей цилиндрической поверхности служит кривая АВ,лежащая в плоскости
Oху,а образующая параллельна оси Оz, то площадь поверхности,задаваемой функцией
z=f(x,y),находится по формуле 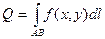 .
.
§2.Криволинейный интеграл 2-го рода.
2.1.Основные понятия.
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдольнекоторой кривой(и других) приводит к понятию криволинейного интеграла 2-го рода,который определяется почти также,как и интеграл 1-го рода.
Пусть на плоскости Оху задана непрерывная кривая АВ (или L) и функция
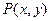 ,определенная в каждой точке кривой. Разобьем кривую АВ точками на п произвольных дуг
,определенная в каждой точке кривой. Разобьем кривую АВ точками на п произвольных дуг  с длинами
с длинами 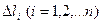 в направлении от точки А к точке В (Рис.1).Выберем на каждой дуге
в направлении от точки А к точке В (Рис.1).Выберем на каждой дуге  произвольную точку
произвольную точку  и составим сумму
и составим сумму
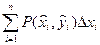 , (2.1)
, (2.1)
где 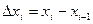 - проекция дуги
- проекция дуги  на ось Ох.
на ось Ох.
 у В=
у В= 
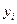
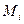
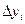
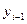

А= 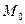
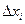
О 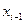
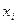 х
х
Рис.1.
Сумму (2.1) называют интегральной суммой для функции Р(х,у) по переменной х.
Определение. Если 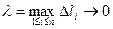 интегральная сумма (2.1) имеет конечный предел,не зависящий ни от способа разбиения кривой АВ, ни от выбора точек
интегральная сумма (2.1) имеет конечный предел,не зависящий ни от способа разбиения кривой АВ, ни от выбора точек 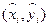 , то его называют криволинейным интегралом по координате х (или 2-го рода) от функции Р(х,у) по кривой АВ и обозначают
, то его называют криволинейным интегралом по координате х (или 2-го рода) от функции Р(х,у) по кривой АВ и обозначают 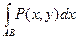 , т.е.
, т.е.
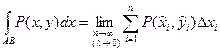 .
.
Аналогично вводится криволинейный интеграл от функции Q(х,у) по координате у:
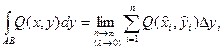 ,
,
где 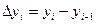 - проекция дуги
- проекция дуги  на ось Оу.
на ось Оу.
Криволинейный интеграл 2-го рода общего вида 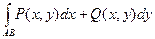
пределяется равенством 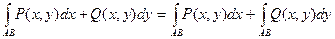 .
.
ТЕОРЕМА. Если кривая АВ гладкая,а функции Р(х,у) и Q(х,у) непрерывны на кривой АВ,то криволинейный интеграл 2-го рода существует.
Основные свойства криволинейного интеграла 2-го рода.
1). При изменении направления пути интегрирования криволинейный интеграл 2-го рода изменяет свой знак на противоположный,т.е. 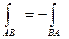 .
.
2). Если кривая АВ точкой С разбита на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям,т.е. 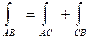 .
.
3).Если кривая АВ лежит в плоскости,перпендикулярной оси Ох, то
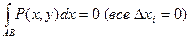 ,
,
Аналогично для кривой,лежащей в плоскости,перпендикулярной оси Оу:
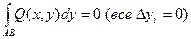 .
.
4).Криволинейный интеграл по замкнутой кривой(обозначается 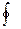 ) не зависит от выбора начальной точки(зависит только от направления обхода кривой).
) не зависит от выбора начальной точки(зависит только от направления обхода кривой).
2.2. Вычисление криволинейного интеграла 2-го рода.
Явное представление кривой интегрирования.
Если кривая АВ задана уравнением 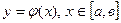 ,где
,где 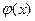 и ее производная
и ее производная 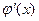 непрерывны на отрезке
непрерывны на отрезке 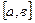 ,то
,то
. 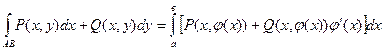 (2.2)
(2.2)
ПРИМЕР. Вычислить 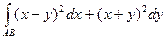 ,где АВ- отрезок прямой между точками О(2,0) и А(4,2).
,где АВ- отрезок прямой между точками О(2,0) и А(4,2).
Уравнение прямой ОА есть: 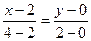 , 2х-4=2у или
, 2х-4=2у или 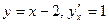 ,
, 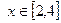 ,тогда
,тогда
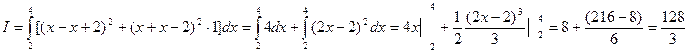 .
.
Параметрическое представление кривой интегрирования.
Если кривая АВ задана уравнениями 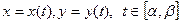 ,где
,где 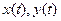 - непрерывны вместе со своими производными,причем точке А соответствует
- непрерывны вместе со своими производными,причем точке А соответствует 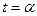 ,точке В- значение
,точке В- значение 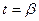 ,то
,то 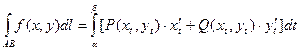 . (2.3)
. (2.3)
2.3. Формула Остроградского-Грина.
Связь между двойным интегралом по области D и криволинейным интегралом по границе L этой области устанавливает формула Остроградского-Грина.
Пусть на плоскости Оху задана область D,ограниченная кривой,пересекающейся с прямыми,параллельными координатным осям не более чем в двух точках,т.е. область D – правильная.
ТЕОРЕМА. Если функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными 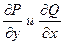 в области D,то имеет место формула
в области D,то имеет место формула
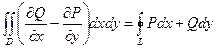 ,
,
где L- граница области D и интегрирование вдоль кривой L производится в положительном направлении(при движении вдоль кривой область D остается слева).
ПРИМЕР. Вычислить с помощью формулы Грина: 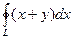 вдоль контура L,который является треугольником с вершинами А(0,0),В(1,0),С(0,1).
вдоль контура L,который является треугольником с вершинами А(0,0),В(1,0),С(0,1).
Найдем 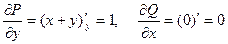 ,уравнения линий АВ:у=0, АС: х=0, ВС:у=1-х, тогда по формуле Грина:
,уравнения линий АВ:у=0, АС: х=0, ВС:у=1-х, тогда по формуле Грина:
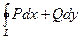 =
=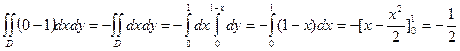 .
.
2.4.Некоторые приложения криволинейного интеграла 2-го рода.
1). Работа переменной силы.
Переменная сила 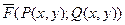 на криволинейном участке АВ производит
на криволинейном участке АВ производит
работу,которая находится по формуле 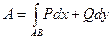 .
.
 у
у  В
В
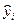
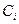
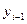

А
О 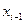
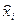
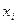 х
х
Рис.2
Замечание. В случае пространственной кривой АВ:
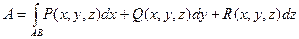 .
.
ПРИМЕР. Найти работу,выполненную силой 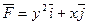 вдоль прямой,которая соединяет точки А(1,2) и В(2,4).
вдоль прямой,которая соединяет точки А(1,2) и В(2,4).
Тогда 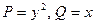 , уравнение прямой АВ:
, уравнение прямой АВ: 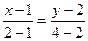 , 2х-2=у-2, у=2х.
, 2х-2=у-2, у=2х.
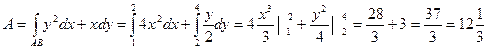 .
.
2). Площадь плоской фигуры.
Площадь плоской фигуры,расположенной в плоскости Оху и ограниченной замкнутой линией L находится по формуле: 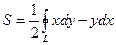 , при этом направление обхода контура выбирается обратным движению часовой стрелки.
, при этом направление обхода контура выбирается обратным движению часовой стрелки.
Глава 15.КОМПЛЕКСНЫЕ ЧИСЛА.
§1.Понятие и представление комплексных чисел.
1.1.Основные понятия.
Определение. Комплексным числом z называется выражение вида 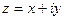 ,
,
где х,у -действительныйе числа, i – мнимая единица (i² = -1).
Если х=0, то число 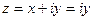 называется чисто мнимым,
называется чисто мнимым,
если у=0,то число 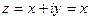 отождествляется с действительным числом,а это означает, что множество всех действительных чисел R является подмножеством множества
отождествляется с действительным числом,а это означает, что множество всех действительных чисел R является подмножеством множества
C всех комплексных чисел (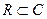 ).
).
Число х – действительная часть комплексного числа z, обозначается  ,
,
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 547; Нарушение авторских прав?; Мы поможем в написании вашей работы!