Поверхностный интеграл 2 рода изменяет знак при перемене стороны поверхности

.

.

.

При делении комплексных чисел их модули,соответственно делятся,а аргументы-вычитаются.

Извлечение корней из комплексных чисел.

Извлечение корня п- ной степени определяется как действие,обратное возведению в натуральную степень.

Определение. Корнем п- й степени из комплексного числа 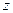называется комплексное число ,удовлетворяющее равенству 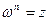, т.е. 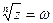,если .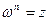

Если положить 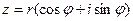,,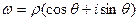то по определению корня и формуле Муавра,получаем:

Отсюда 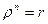,,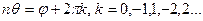 т.е .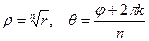

Поэтому равенство 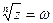принимает вид:

Получим п различных значений корня.При других значениях k,в силу периодичности косинуса и синуса,получатся значения корня,совпадающие с уже найденными.

ПРИМЕР. Найти значения а). 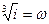, в). .

а). Запишем i в тригонометрической форме: , ,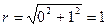

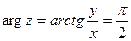тогда ,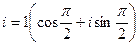

При k=0 имеем: ,

k=1 имеем: ,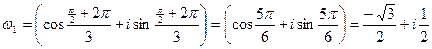

k=2 имеем: .

в). Запишем -1 в тригонометрической форме: , ,

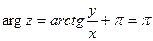тогда ,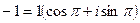

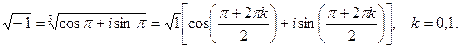
При k=0 имеем: ,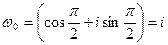

k=1 имеем: ,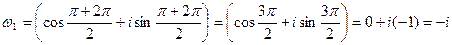

Глава 16.ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.

Обобщением двойного интеграла является так называемый поверхностный.

§1.Поверхностные интегралы I рода.

1.1.Основные понятия.

_z n

P_i∆σ_yz

σ_i

σ ∆σ_{xz ∆σi} ∆σ

_x ∆σ_xy ^y

Рис.1. Рис.2

Пусть в точках некоторой поверхности σ с площадью σ пространства OXYZ определена непрерывная функция f(x,y,z). Разобьем поверхность σ на n частей σ_i,

площади которых обозначим через ∆σ_i, а диаметры - через d_i (i =1,2… n).

В каждой части σ_i возьмем произвольную точку P_i и составим сумму

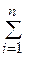f(x_i ,y_i ,z_i ) ∆σ_i

Она называется интегральной для функции f(x,y,z) по поверхности σ.

Определение. Поверхностным интегралом первого рода от функции

f(x,y,z) по поверхности σ называется предел интегральной суммы(если он существует)

f(x,y,z) dσ = 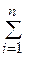f(x_i ,y_i ,z_i ) ∆σ_i

гдe ∆σ_i площадь элемента i-ого поверхности σ,которой принадлежит точка

(x_i ,y_i ,z_i ) при λ=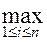 ∆d_i →0( тогда n→∞).

ТЕОРЕМА существования. Если поверхность σ гладкая(в каждой ее точке существует

касательная плоскость,которая непрерывно меняется с перемещением точки по поверхности),

а функция f(x,y,z) непрерывна на этой поверхности,то поверхностный интеграл существует.

Основные свойства поверхностного интеграла 1 рода.

1). 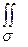kf(x,y,z)dσ = k 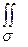f(x,y,z)dσ,где k-число.

2). 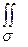[ f₁(x,y,z)± f₂(x,y,z)]dσ =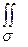f₁(x,y,z)dσ ± 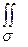f₂(x,y,z)dσ

3). Если поверхность разбита на 2 части σ₁ e σ₂, то:

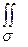f(x,y,z)dσ =f(x,y,z)dσ +f(x,y,z)dσ

4).Если на поверхности выполнено неравенство f₁(x,y,z) ≤ f₂(x,y,z),то

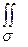f₁(x,y,z) dσ ≤ 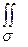f₂(x,y,z) dσ.

5). 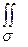dσ = σ,где σ – площадь поверхности σ.

6). |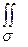f(x,y,z) dσ | ≤ 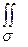|f(x,y,z)|dσ.

7).(Теорема о среднем значении) Если f(x,y,z) непрерывна на поверхности σ,

то на этой поверхности существует точка (x_c,y_c,z_c) такая,что

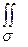f(x,y,z) dσ = f(x_c,y_c,z_c)*σ.

1.2.Вычисление поверхностного интеграла 1 рода.

Вычисление поверхностного интеграла 1 рода сводится к вычислению двойного

интеграла по области D - проекции поверхности σ на плоскость ОХУ.

σ_i 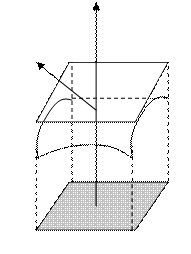OXY

Как и в только что рассмотренном случае разобьем поверхность σ на n частей σ_i,

и возьмем в плоскости ОХУ ( область D) произвольную точку С_i. При

этом область D окажется разбитой на n частей σ_xy i. Из произвольной точки С_i

восстановим перпендикуляр к плоскости ОХУ до пересечения с поверхностью σ –

получим точку М(x_i ,y_i ,z_i) проведем через нее касательную плоскость и рассмотрим

ту ее часть Тi,которая на плоскость ОХУ проектируется в област σ_xy i. Получаем площади элементарных частей σ_i, Тi, σ_xy i,которые обозначим через ∆σ_i, ∆Тi, ∆σ_xy i соответственно.

Будем приближенно считать,что

∆ Тi ≈ ∆ σ_i.

Обозначим через γ i отрый угол между осью OZ и нормалью к поверхности в

точке М_i, получаем: ∆ Тi *cos γi ≈ ∆σ_xy i.

Область ∆σ_xy i есть проекция Тi на плоскость ОХУ.

Если поверхность σ задана уравнением z=z(x,y),то уравнение касательной

плоскости в точке Сi: ,

где - координаты нормального вектора к плоскости.

Острый угол γi есть угол между векторами 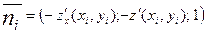и=(0,0,1).

Косинус угла между ними равен:

cos γi = =1/ .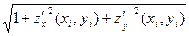

Тогда равенство принимает вид:

∆ Тi ≈ ∆σ_xy i / cos γi = ∆σ_xy i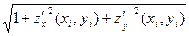

Переходя к пределу при стремлении к нулю наибольшего диаметра σ_i, а

следовательно и его проекции σ_xy I, получаем формулу,выражающую

интеграл по поверхности σ через двойной интеграл по проекции σ на плоскость ОХУ:

∫ ∫ f(x,y,z) dσ = ∫ ∫ f(x,y, z(x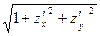,y)) dxdy

^{σ σxy}

Отметим,что если поверхность σ задана уравнением вида у=у(х, z) или

х=х(у, z),то аналогично получим:

∫ ∫ f(x,y,z) dσ = ∫ ∫ f(x, y(х,z), z) dxdz

^{σ σ xz}

∫ ∫ f(x,y,z) dσ = ∫ ∫ f(x(y,z),y, z)) dydz.

^{σ σ yz}

ПРИМЕР. Вычислить ∫ ∫ dσ, гдe σ - часть параболоида

^σ

вращения z=1-x²-y², ограниченного поверхностью z=0 (Рис.3).

_{z y}

^x

^{x 1 Рис.3 y Рис.4}

Решение:

Поверхность σ имеет проекцию на плоскости OXY, которая ограничена кругом x²+y²=1(z=0) с радиусом R=1 (Рис.4).

Найдем производные : z’_x(x,y)= -2x; z’_y(x,y)= -2y. ( при z = φ(x,y)):

По формуле:

∫ ∫ f(x,y, φ(x,y)) dxdy =

D

∫ ∫ dxdy = ∫ ∫ (1+4x²+4y²)dxdy.

D D

Используя полярные координаты: x=rcosφ, y=rsenφ, находим

_{2π 1 2π 1}

∫ ∫ (1+4x²+4y²)dxdy= ∫ dφ ∫ (1+4r²)rdr = ∫ dφ [r²/2+r⁴] =

^{S 0 0 0 0}

_2π

1,5 ∫dφ = 1,5( 2π-0) = 3π.

⁰

ПРИМЕР: Вычислить ∫ ∫ x(y+z) dσ, гдe σ - часть цилиндрической поверхности

^σ

х=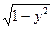,отсеченной плоскостями z=0,z=2 (Рис.5). z

_{z 2 y}

^{x 1 Рис.5 y Рис.6}

Решение:

Почему имеем только 0,5 циллиндра? Из уравнения х=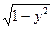, следует,что это часть круга,где х принимает только положительные значения.

Поверхность σ имеет проекцию на плане OZY в области D-прямоугольник, который ограничен линиями z=0,z=2 и кругом x²+y²=1(z=0). D (Рис.6).

Найдем производные : (x’_y)=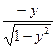; (x’_z)=0

По формуле:

∫ ∫ f(x,y,z) dσ = ∫ ∫ f(x,y,z) dσ = ∫ ∫ f(x(y,z),y, z)) dydz =

^{σ σ yz}

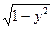= ∫ ∫(у+ z)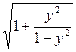dydz = ∫ ∫ (у+ z) dydz = 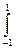dy(у+z)dz =

^{σ yz σ yz}

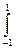⁼ (у z +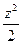)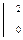dy=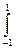(2у+2) dy=(у²+2у) =1+2-1+2=4.

§2.Поверхностные интегралы II рода.

2.1.Основные понятия.

Поверхностный интеграл II рода строится по образцу криволинейного интеграла

II рода, где направленную кривую разлагали на элементы и проектировали их на

координатные оси; знак брали в зависимости от того, совпадало ли ее направление с

направлением оси или нет.

Пусть задана двусторонняя поверхность ( таковой является плоскость, эллипсоид,

любая поверхность,задаваемая уравнением z=f(x,y),где сама функция и ее производные непрерывны в некоторой области D плоскости ОХУ).

После обхода такой поверхности,не пересекая ее границы, направление

нормали к ней не меняется. Примером односторонней поверхности является так называемый

лист Мебиуса,получающийся при склеивании сторон АВ и СД прямоугольника АВСД так,

что точка А совмещается с точкой С,а В - с Д.

В С

А Д

Пусть в точках рассматриваемой двусторонней поверхности σ в пространстве

ОХУZ определена непрерывная функция f(x,y z). Выбранную сторону поверхности

(в таком случае говорят,что поверхность ориентирована) разбиваем на части σ i,

где ( i =1,2… n) и проектируемих на координатные плоскости.

При этом площадь проекции ∆ σ i берем со знаком:

- плюс,если выбрана верхняя сторона поверхности,или,что то же

самое, если нормаль 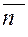к выбранной сторонеповерхности составляет

с осью ОZ острый угол, т.е. (cosγ >0) и

- минус,если выбрана нижняя сторона поверхности (cosγ <0).

В этом случае интегральная сумма имеет вид:

,где ∆ σ хуi –площадь проекции σ на плоскость ХОУ.

Определение. Предел интегральной суммы,если он существует и не зависит

от способа разбиения поверхности σ на части σ i и от выбора точек C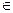i σi

называется поверхностным интегралом II рода (по координатам) от

функции f(x,y z) по переменным х и у по выбранной стороне поверхности и

обозначается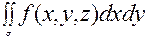

Тогда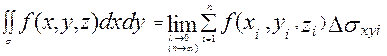

Аналогично определяются поверхностные интегралы 2 рода по переменным

y, z и z,x: ,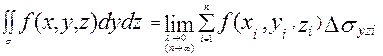

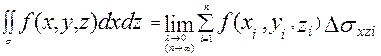
Общим видом поверхностного интеграла 2 рода служит интеграл(связь между

поверхностными интегралами I и II рода):

∫ ∫ P(х,у,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy= ∫ ∫[Pcos α + Qcosβ + Rcosγ] dσ (1)

^{σ + σ}

Отметим,что если σ – замкнутая поверхность,то поверхностный интеграл по внешней стороне ее обозначается ,по внутренней- .

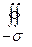Из определения поверхностного интеграла II рода вытекают следующие свойства:

2).Постоянный множитель можно выносить за знак поверхностного интеграла.

3).Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.

4) Поверхностный интеграл II рода по всей поверхности σ= σ1+σ2 равен сумме интегралов по ее частям σ1 и σ 2,если σ1 и σ 2 пересекаются только по границе,их разделяющей.

5).Если σ1, σ2,σ3 - цилиндрические поверхности с образующими, параллельными соответственно осям OX,OY,OZ,то

∫ ∫R(x,y,z)dxdy= ∫ ∫ P(x,y,z)dydz= ∫ ∫Q(x,y,z)dzdx=0.

σ1 σ2σ3

2.2.Вычисление поверхностного интеграла II рода.

Вычисление поверхностного интеграла 2 рода сводится к вычислению двойного интеграла.

Пусть функция R(x,y,z) непрерывна во всех точках поверхности σ заданной уравнением z= z (x,y), где z (x,y)- непрерывная функция в замкнутой области D ( или Dху) – проекция поверхности σ на ОХУ.

Выберем сторону поверхности σ,где нормаль к ней образует с осью Оz острый угол, тогда получим результат со знаком (+),

если выбрать вторую сторону поверхности,т.е. нижнюю,(тупой угол) то

полученный интеграл будет со знаком (-).

∫ ∫R(x,y,z)dxdy = ± ∫ ∫ R(x,y,z(x,y)) dxdy (2)

^{σ + Dху}

Аналогично: если поверхность задана уравнением у=у(х,z)

∫ ∫Q(x,y,z)dzdx = ± ∫ ∫Q(x,y(x,z),z)dzdx (3)

^{σ + Dxz}

и если поверхность задана уравнением х=х(у,z)

∫ ∫ P(x,y,z)dydz = ±∫ ∫P(x(y,z),y,z)dydz. (4)

^{σ + Dyz}

Для вычисления общего поверхностного интеграла II рода используются выше рассмотренные формулы,проектируя поверхность на все три координатные плоскости:

∫ ∫ P(х,у,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy=

^{σ +}

= ±∫ ∫P(x(y,z),y,z)dydz ± ∫ ∫Q(x,y(x,z),z)dzdx ± ∫ ∫ R(x,y,z(x,y)) dxdy.

^{Dyz Dxz Dху}

Если поверхность σ дана в форме F(x,y,z)=0,то косинусы

нормального вектора этой поверхности определяются по формулам:

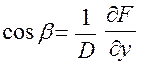; ; ,где

D = ± ,

И выбирается знак перед радикалом в зависимости от поверхности внутренней или внешней.

Справедливо равенство:

cosα* dσ = dydz; cosβ* dσ = dzdx; cosγ * dσ = dxdy.

где dσ – элемент площади поверхности σ; cosα, cosβ, cosγ - направляющие косинусы нормали 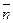к выбранной стороне поверхности σ.

Если вычисление какого-либо из 3 интегралов уравнения поверхности

нельзя записать в форме адекватной, необходимо разделить поверхность на части и

считать как сумму интегралов.

По свойствам, если в интеграле между частями цилиндрической поверхности

образующие параллельны, например оси OZ, интеграл

∫ ∫ RcosγdS равен нулю, поскольку нормаль перпендикулярна образующей и

γ=π/2; cosγ=0.Также равна нулю и левая часть формулы (1),

потому что проекция на плоскость OXY - линия, не область.

Можно сделать аналогичное заключение и для других осей,если в интеграле

образующие части цилиндрической поверхности параллельны каким-либо другим осям.

ПРИМЕР: Вычислите ∫ ∫ xdydz+dzdx+xz²dxdy, если S

^S

верхняя часть сферы x²+y²+z²=1 в I октанте.

Решение:

Проекции на плоскости z

соответственно

D₁,D₂,D₃ , они являются ¼ части D₂ D₁

кругов с радиусом 1.

x D₃ y

I₁ = 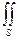xdydz = ,

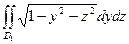I₂ = 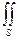dxdz = 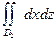, I₃ = 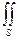xz²dxdy = /

Используем полярные координаты: y=rcosφ,z=rsenφ, 0≤θ≤π/2

I₁ = .

I₂ = .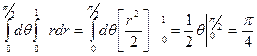

В полярных координатах: х=rcosφ,у=rsenφ, 0≤θ≤π/2

I₃ = .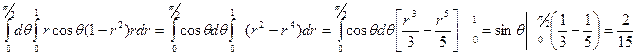

I = I₁+I₂+I₃ = π/6 + π/4+2/15 = 5π/12 + 2/15.

ПРИМЕР: Вычислите ∫ ∫ -xdydz+zdzdx+5dxdy по верхней стороне части плоскости

^S

2х-3у+z=6, лежащей в IVоктанте. z

_y

_x

Знаем,что если поверхность σ дана в форме F(x,y,z)=0,то косинусы

нормального вектора этой поверхности определяются по формулам:

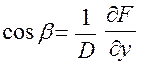; ; ,где

D = ± ,

И выбирается знак перед радикалом в зависимости от поверхности -внутренней или внешней.

Тогда , ,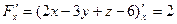

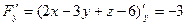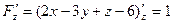
и нормальный вектор плоскости равен .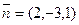

Вычислим направляющие косинусы: ,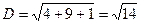

, , ,

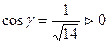Поэтому перед двойным интегралом в формулах (2),(4) следует брать знак «+»,а в формуле (3) – знак «-».

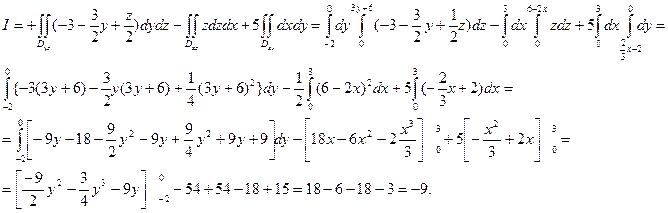
2.3.Формула Остроградского-Гаусса.

Связь между поверхностным интегралом II рода по замкнутой поверхности

и тройным интегралом по обьему,ограниченному этой поверхностью

устанавливает следующая Теорема.

Если функции P, Q, R непрерывны вместе со своими частными производными

первого порядка в пространственной области V, то имеет место формула (1):

.

гдe =( cosα,cosβ,cosγ)-вектор нормали к поверхности S и S -граница области V

и интегрирование по S производится по ее внешней стороне.

Формула (1) называется ФОРМУЛОЙ ОСТРОГРАДСКОГО-ГАУССА (является

аналогом формулы Остроградского-Грина).

Замечание. 1).Формула (1) справедлива для любой области V,которую можно разбить на конечное число областей рассмотренного вида.

2).Формулу Остоградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.

ПРИМЕР: Если поверхность S ограничивает область кубическую T, используя

формулу Остроградского-Гаусса (1), получим:

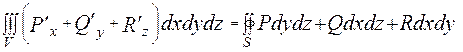
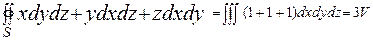, гдe V - обьем тела.

Глава 17. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ.

§1.Основные понятия.

Теория поля – крупный раздел физики,механики,математики,в котором изучаются скалярные,векторные,тензорные поля.

К рассмотрению скалярных и векторных полей приводят многие задачи физики,электротехники, математики, механики и др.технических дисциплин.

Изучение одних физических полей способствует изучению других.Так например,силы всемирного тяготения,магнитные,электрические силы- все они изменяются обратно пропорционально квадрату расстояния от своего источника,вид силовых линий напоминает картину обтекания препятствий жидкостью и т.д.

Математическим ядром теории полдя являются такие понятия,как градиент,поток,потенциал,дивиргенция,ротор,циркуляция и др.Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.

Определение. Полем называется область V пространства,в каждой точке которой определено значение некоторой величины. Если каждой точке Р этой области соответствует определенное число u=f(P) = f(x,y,z),гдe P(x,y,z) говорят,что в области определено или задано скалярное поле(или функция точки).Иначе говоря,скалярное поле- это скалярная функция u=f(P) вместе с ее областью определения.

Если же каждой точке Р области пространства соответствует некоторый вектор а=а(Р),то говорят,что задано векторное поле(или векторная функция точки).

ПРИМЕРЫ СКАЛЯРНЫХ ПОЛЕЙ:

температуры(воздуха,тела…),

атмосферного давления,плотности(массы,воздуха…) и т.д.

ПРИМЕРЫ ВЕКТОРНЫХ ПОЛЕЙ:

поле силы тяжести,

поле скоростей частиц текущей жидкости(ветра)

магнитное поле, и т.д.

§2.Скалярное поле.

Определение. Стационарным (установившимся) называется

скалярное(векторное) поле,если функция u=f(P) не зависит от времени.

Определение. Нестационарным (неустановившимся) называется

скалярное(векторное) поле,которое меняется с течением времени.

Далее рассматриваем только стационарные поля.

Запись поля возможно производить как в форме u=f(P) = f(x,y,z), так и

U=U(r), где r- радиус-вектор точки Р.

Определение. Плоским называется скалярное поле U(х,у),т.е. когда скалярная функция зависит только от 2 переменных х,у.

Аналогично: вектор 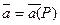,определяющий векторное поле,можно рассматривать как векторную функцию трех скалярных аргументов x,y,z: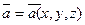

или .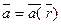

Вектор можно представить в ви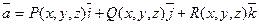де:

, где

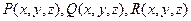- проекции вектора а на оси координат.

Если одна из проекций вектора равна нулю, а две другие зависят только от 2 переменных, то векторное поле называется плоским,например, .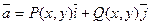

Определение. Векторное поле называется однородным,если 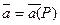- постоянный вектор.т.е. P,Q,R - постоянные величины.Пример: поле тяжести – P=0,Q=0,R=-mg,

где g –ускорение силы тяжести, m -масса точки.

В дальнейшем считаем,что скалярные функции 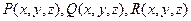непрерывны вместе со своими частными производными.

ПРИМЕРЫ:

1).Функция u= определяет скалярное поле в точках пространства, ограниченного сферой с центром в начале координат и радиусом r=1.

2). скалярное поле u=определено во всем пространстве, за исключением точек оси OZ(на ней х²+у²= 0).

Рассмотрим скалярное поле задаваемое функцией u= u(x,y,z).

Для наглядного представления скалярного поля используем поверхности и линии уровня.

Определение. Поверхностью уровня скалярного поля называется геометрическое место

точек,в которых функция принимает постоянное значение, т.е. f(x,y,z)=C, (1)

гдe C=constante.

Придавая в уравнении (1) величине С различные значения,получаем различные поверхности уровня,которые в совокупности как бы расслаивают поле.Через каждую точку поля проходит только одна поверхность уровня.Ее уравнение находят путем подстановки координат точки в уравнение (1).

Для скалярного поля,образованного функцией и = ,поверхностями

уровня является множество концентрических сфер с центрами в начале координат:

=С. При С=1 сфера представляет собой точку.

В случае плоского поля равенство f(x,y) = C представляет собой собой

уравнение линии уровня поля,т.е. линия на плоскости ОХУ,в точках которой функция

f(x,y) = C сохраняет постоянное значение.

В метеорологии,например,сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.

Линии уровня используются в математике при исследовании поверхностей методом сечений.

На рисунках представлены примеры,

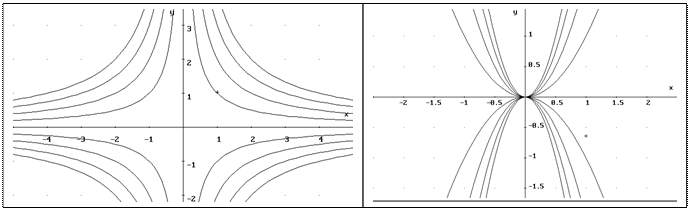
U=xy U=y/x²

(1=xy,-1=xy,2=xy,-2=xy,…) (1=y/x², -1= y/x², 2=y/x²,…)

U=r² U=1/r

(x²+y²=1, x²+y²=2, x²+y²=3,…) (x²+y²=1,x²+y²=1/2, x²+y²=1/3,…)

§3.Векторное поле.

Рассмотрим векторное поле,задаваемое вектором 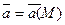.Простейшей геометрической характеристикой поля являются векторные линии.

Определение. Векторной линией поля (линии силы,..) называется линия,касательная

к которой в каждой ее точке М имеет направление соответствующего ей вектора

Дата добавления: 2014-01-15