Линейность

Y

М).

Это понятие для конкретных полей имеет ясный физический смысл. Например,

в поле скоростей текущей жидкости векторными линиями

будут линии,по которым движутся частицы жидкости(линии тока);

-для магнитного поля векторными(силовыми) линиями будут линии,выходящие

из северного полюса и оканчивающиеся в южном.

Совокупность всех векторных линий поля,проходящих через некоторую замкнутую кривую,называется векторной трубкой.

С изучения векторных линий начинают изучение векторного поля. Векторные линии

поля 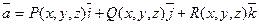описываются системой дифференциальных

уравнений вида . (2)

ПРИМЕР. Найти векторные линии поля линейных скоростей тела,вращающегося с постоянной угловой скоростью ω вокруг оси Оz, т.е.поле определено вектором

V=-ωy i + ωx j.

Согласно формуле (2) имеем: .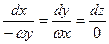

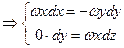Проинтегрируем: 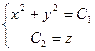,т.е векторные линии поля – окружности с центрами на оси Оz, лежащие в плоскостях, перпендикулярных к этой оси.

3.1.Поток поля.

Пусть векторное поле образовано вектором .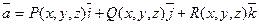

Для наглядности считаем,что вектор 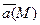- вектор скорости некоторого потока жидкости, движущейся стационарно.Представим,что некоторая поверхность S находится в этом потоке и пропускает жидкость.

Определение. Потоком вектора через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали n (cosα,cosβ,cosγ) к поверхности,т.е.

,

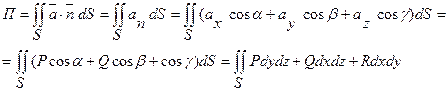учитывая,что .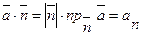

Замечание. Поток П вектора 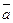есть скалярная величина,равная объему жидкости, которая протекает через поверхность S за единицу времени.В этом состоит физический смысл потока(независимо от физического смысла поля).

Особый интерес представляет случай,когда поверхность S замкнута и ограничивает некоторый обьем V, тогда поток вектора записывается в виде

Π=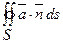

В этом случае за направление вектора 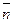обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S (см рис.1).

Рис.1,2

Если векторное поле есть поле скоростей текущей жидкости,то величина потока Π через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области V (обьема V) и втекающей в нее за единицу времени(в точках поверхности S,где векторные линии выходят из обьема V,внешняя нормаль образует с вектором 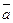острый угол и 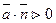,а в точках,где векторные линии входят- ).

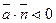При этом если Π>0, то из области V вытекает больше жидкости, чем в нее втекает.Это означает,что внутри области имеются дополнительные источники.

Если Π <0, то внутри области имеются стоки, поглощающие избыток жидкости.

Можно сказать, что источники- точки, откуда векторные линии начинаются, а стоки- точки,где векторные линии кончаются.Так,в электростатическом поле источником является положительный заряд, стоком - отрицательный заряд магнита (Рис.2).

Если Π=0, то из области V вытекает столько же жидкости,сколько в нее втекает в единицу времени;внутри области либо нет ни источников,ни стоков,либо они такие,что их действие взаимно компенсируется.

ПРИМЕР. Найти поток вектора 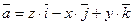через верхнюю сторону треугольника, полученного при пересечении плоскости 3х+6у-2z-6=0 с координатными плоскостями.

Решение:

z

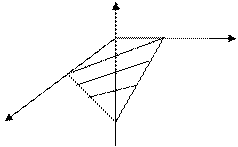
x -3

Воспользуемся формулой 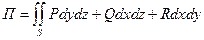, тогда Р=z,Q=-х,R=y.

,поток найдем методом проектирования на три координатные

плоскости.

Знаем,что если поверхность σ дана в форме F(x,y,z)=0,то косинусы

нормального вектора этой поверхности определяются по формулам:

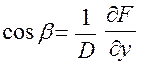; ; ,где

D = ± ,

И выбирается знак перед радикалом в зависимости от поверхности -внутренней или внешней.

Тогда , ,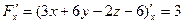

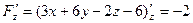
и нормальный вектор плоскости равен .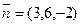

Вычислим направляющие косинусы: ,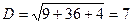

, , .

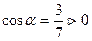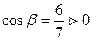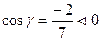Нормаль к верхней стороне треугольника образует с осью Ох и Оу тупые углы,а с осью Оz – острый угол.(Единичный вектор данной плоскости есть 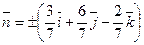; на верхней стороне 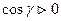,поэтому надо выбирать знак

«-»,получим , , ).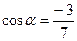

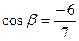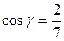Тогда :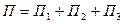

,

,

.

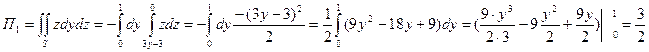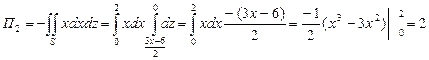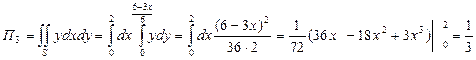Итак, .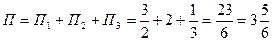

3.2.Циркуляция поля.

Определение. Циркуляцией векторного поля ,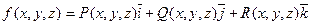

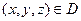вдоль замкнутой дуги L c с указанным дополнительным направлением называют криволинейный интеграл .

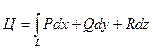Если Ц=0,когда 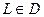,то поле 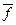является потенциальным.

Физический смысл циркуляции: если дуга L расположена в силовом поле, то циркуляция -это работа силы поля при перемещении материальной точки вдоль

дуги L.

Возможны различные формы записи циркуляции:

,

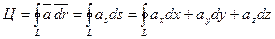где a_S есть проекции вектора a на касательную к L.

▪ Если кривая замкнутая С ограничивает поверхность (внешняюю и внутреннюю) S, то справедлива формула СТОКСА, в векторной форме:

Ц =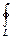 a dr = 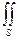n rot a dS=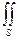(rot a)_n dS= 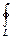Pdx+Qdy+Rdz, гдe

n - векторнормали к поверхности S.

ПРИМЕР. Вычислить циркуляцию векторного поля 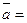(x-2z)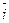+(x+3y+z)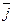+(5x+y)

вдоль периметра треугольника с вершинами А(1,0,0), В(0,1,0), С(0,0,1).

z C

х A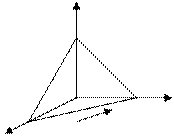B у

Решение:

Согласно формуле Ц =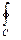 a dr = 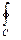Pdx+Qdy+Rdz=

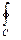(x-2z)dx +(x+3y+z)dy +(5x+y)dz= + +

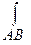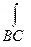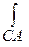
На отрезке АВ: х+у=1, z=0, следовательно, y=1-x, dy=-dx, dz=0

= (х-0)dx+(x+3-3x+0)*(-dx)+0 =xdx+2xdx-3dx=3xdx-3dx =

[3x²/2 - 3x] = 0-3/2-0+3= 3/2 =1,5

На отрезке BC: х=0, у + z=1, следовательно, z=1-y, dy=-dx, dx=0

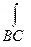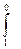=(0-2+2y)*0 +(0+3y+1-y)dy+(0 +y)(-dy)= 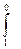2ydy+dy -ydy=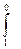ydy+dy=

[ y²/2+y ] = 0-½ +0-1 = -3/2=-1,5

На отрезке CA: y=0, x + z=1, следовательно, z=1-x, dy=0, dz=-dx

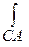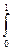=(x-2+2x)dx +0 +1(5x+0)(-dx)= 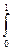3xdx-2dx-5xdx =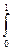(-2)xdx – 2dx=

[(-2)x²/2 -2x ] 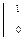= -1-0 -2+0 = -3

Ц = 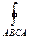= 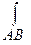+ + 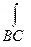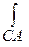==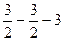 -3.

3.3.Ротор поля.Формула Стокса.

Определение. Ротором (или вихрем) векторного поля

a = Р(x,y,z) i + Q(x,y,z) j + R(x,y,z) k

называется вектор,обозначаемый rot a (М) и определяемый формулой

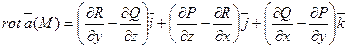
Эту формулу можно записать с помощью символического определителя в виде,удобном для запоминания:

.

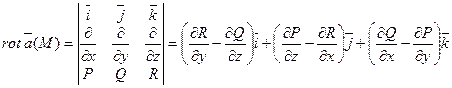ПРИМЕР. Найти ротор векторного поля

f = x ²i + y ²j - z ²k. P= x ²; Q=y ²; R = -z ²;

P ´_x = 2x ; Q ´_y =2y ; R ´_z = - 2z;

rot f =( R ´_y- Q ´_z)i+( P´ _z - R´ _x)j + ( Q´ _x - P ´_y)k =0.

Свойства ротора.

1). Если a – постоянный вектор,то rot a =0.

2). rot(С· a )=С· rot a,где С=постоянная.

3). rot (a+в) = rot a + rot в.

Используя понятие ротора и циркуляции векторного поля,запишем

Формулу Стокса (англ.математик,физик)

.

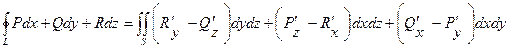Левая часть формулы представляет собой циркуляцию вектора a по контуру L, интеграл

в правой части формулы –поток вектора rot a через поверхность S,ограниченную

контуром L. Данная формула устанавливает связь между поверхностными и

криволинейными интегралами II рода.

ПРИМЕР: Вычислить 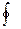x²y³dx+dy+zdz, гдe L ограничена окружностью

^L

x²+y²=1,z=0 и поверхность S -верхняя часть полусферы x²+y²+y²=1 (z>0) с контуром L (с позитивным направлением).

Решение:

Используя формулу Стокса:

Pdx+Qdy+Rdz = 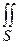(Q´_x- P´_y)dxdy+(R´_y-Q´_z)dydz +(P´_z-R´_x) dzdx

P= x²y³, Q=1, R=z

(Q’_x- P’_y)= -3x²y² ; (R’_y-Q’_z)=0; (P’_z-R’_x)=0

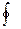Pdx+Qdy+Rdz= 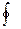x²y³ dx+dy+zdz = - 3 ∫∫ x²y² dx

^{K K S}

Используя полярные координаты: x=rcosφ, y=rsenφ, найдем

_{2π 1 2π 1}

-3 ∫ dφ ∫ r²cos²φ r²sen²φ rdr =-3 ∫cos²φ sen²φ dφ [r⁶/6] =

^{0 0 0 0}

_{2π 2π}

(-1/2) ∫(1/4)sen²2φdφ=(-1/8)0,25[2φ-senφcosφ] = (-1/32)[4π – sen2 πcos 2 π-0+0]= -π/8.

^{0 0}

[ Используем формулу из Таблицы: sen2φ=2senφcosφ;

∫ sen²ахdx= (1/2)x- (1/4а)senxcosx ].

Производная по направлению и градиент скалярной функции.

Определение. Производной по направлению l единичного вектора 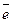скалярной функции 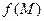в точке 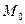называют число .

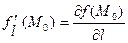Если функция 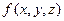дифференцирована в точке 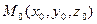и 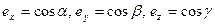- направляющие косинусы единичного вектора 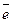, то

существует производная по направлению 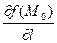,при чем

.

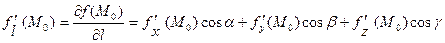При этом вектор 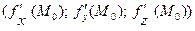называют градиентом функции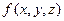

в точке 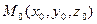и обозначают 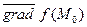, т.е.

.

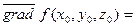
Дивергенция векторного поля.

Соленоидальное и потенциальное поле.

Определение. Дивергенцией векторного поля f (M) = Р(x,y,z) i + Q(x,y,z) j + R(x,y,z) k в

точке М называют число 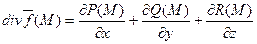,которое является скалярным

произведением вектора набла .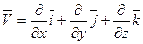

Определение. Если 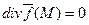во всех точках векторного поля 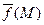,то векторное

поле называется соленоидальным. Это означает,что такое поле не имеет ни

стоков,ни источников(или есть стоки и источники,но они уравновешиваются).

Пример:магнитное поле,создаваемое прямолинейным проводником,вдоль которого

течет электрический ток.

Определение. Если rot f =0 во всех точках поля,то векторное поле называется

потенциальным (или безвихревым или градиентным). Пример:электрическое поле

напряженности точечного заряда.

Потенциал векторного поля находится по формуле:

,

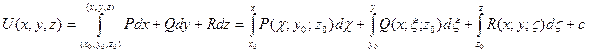где 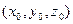- координаты фиксированной точки, (х,у,z)- координаты произвольной точки.Потенциал определяется с точностью до произвольного постоянного слагаемого.

ПРИМЕР.. Плоское векторное поле f (M) = (x+y) i + (x-y) j, (x,y) Є IR является

потенциальным.

Функции P(x,y) e Q(x,y) – дважды дифференцированы в односвязной области D=R²,

P _y ´ =(x+y) _y´ =1=Q _x ´ =(x-y) _x´ для x и y ,поэтому rot f (x,y)=0:

rot f (M) =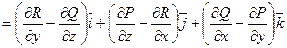

= (0-0) i + (0-0) j +(1-1) k = 0.

Дивергенция поля равна: div f (x,y)= P _x´ +Q _y´ = 1 – 1 = 0.

Итак,данное поле является и потенциальным,и соленоидальным,поэтому оно является

и гармоничным.

Глава 18. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ.

Операционное исчисление играет важную роль при решении прикладных задач,особенно в современной автоматике и телемеханике.

Операционное исчисление - один из методов математического анализа,позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений,содержащих эти операторы, к рассмотрению более простых алгебраических задач.

Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи:

1.От искомых функций переходят к некоторым другим функциям–их изображениям.

2.Над изображениями производят операции,соответствующие заданным операциям над самими функциями.

3.Получив некоторый результат при действиях над изображениями,возвращаются к самим функциям.

Преобразования, которые позволяют перейти от функции к их изображениям,

называют преобразованиями Лапласа.

§1.Преобразования Лапласа.

1.1.Оригиналы и их изображения.

Рассмотрим понятия функции-оригинала и функции-изображения.

Пусть 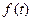- действительная функция действительного переменного 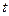(под 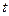понимаем время или координату).

Определение. Функция 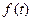называется оригиналом, если она удовлетворяет следующим

условиям:

1. .

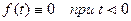2. 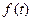- кусочно-непрерывная при 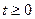,т.е. она непрерывна или имеет точки разрыва

I рода, причем на каждом конечном промежутке оси 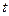таких точек лишь конечное число.

3.Существуют такие числа ,что для всех 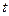выполняется неравенство 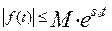,т.е. при возрастании 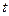функция 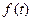может возрастать не быстрее некоторой показательной показательной функции. Число 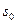называется показателем роста .

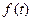Данные условия выполняются для большинства функций,описывающих различные физические процессы.

Первое условие означает,что процесс начинается с некоторого момента времени;

удобнее считать,что в момент 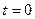.Третьему условию удовлетворяют ограниченные функции

(для них можно положить 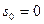,степенные и другие (для функций вида

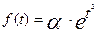условие 3 не выполняется).Не является оригиналом,напрмер, функция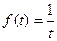

(не удовлетворяет второму условию).

Замечание. Функция 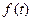может быть и комплексной функцией действительного переменного

,т.е. иметь вид 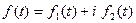; она считается оригиналом,если действительные функции

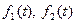являются оригиналами.

Определение. Изображением оригинала 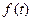называется функция 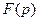комплексного переменного ,определяемая интегралом

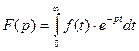(1.1)

Операцию перехода называют преобразованием Лапласа. Соответствие между оригиналом 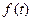и изображением 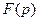записывается в виде 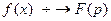или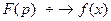

(оригиналы изображаются малыми буквами,а их изображения-соответствующими большими).

TEOРEMA . (существование изображения). Для всякого оригинала 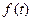изображение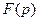

существует(определено) в полуплоскости 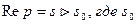- показатель роста функции ,

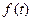при чем функция 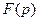является аналитической в этой полуплоскости ().

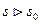σ

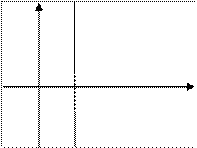
Re p>s0

O s0 s

Рис.1

Докажем первую часть теоремы.Пусть 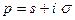произвольная точка

полуплоскости 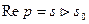.Учитывая,что 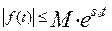, находим:

,

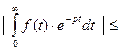
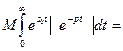
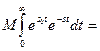
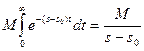т.к.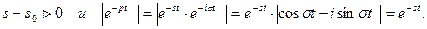

Тогда .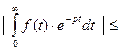

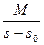Отсюда вытекает абсолютная сходимость интеграла(1.1),т.е. изображение 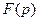существует

и однозначно в полуплоскости .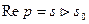

Следствие. (необходимый признак существования изображения). Если функция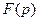

является изображением функции 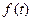,то

.

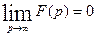TEOРEMA . (о единственности оригинала). Если функция 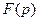служит изображением двух оригиналов 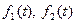,то эти оригиналы совпадают друг с другом во всех точках,в которых

они непрерывны.

ПРИМЕР. Найти изображение единичной функции Хевисайда .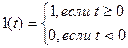

1(t)

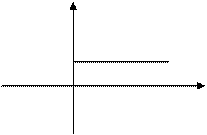
 1  t

Рис.2

формуле 1.1 имеем: 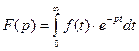=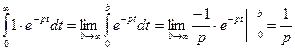. (1.2)

Замечание. В дальнейшем функцию-оригинал будем кратко записывать в виде 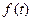,подразумевая,что .

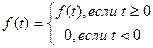ПРИМЕР. Найти изображение функции 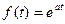,где а- любое число.

Данная функция является оригиналом. По формуле 1.1: =,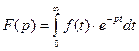

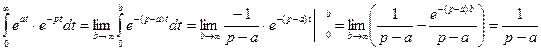если 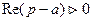,тогда 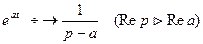. (1.3)

ПРИМЕР. Найти изображение функции .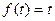

=,

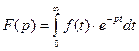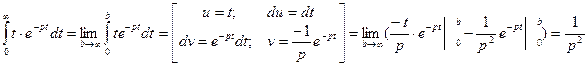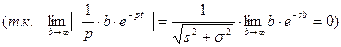т.е. 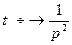. (1.4)

Замечание. Функция 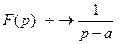является аналитической не только в полуплоскости

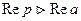,где интеграл (1.1) сходится,а на всей комплексной плоскости р,кроме точки р=а.

Такая особенность наблюдается и для многих других изображений.Далее для нас будет более важным,как правило,само изображение функции,а не область,в котором оно выражается интегралом (1.1).

1.2.Свойства преобразования Лапласа.

Находить изображения, пользуясь только определением изображения не всегда

просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу

нахождения изображений для большого числа разнообразных функций,а также задачу

отыскания оригиналов по их изображениям.

Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений,т.е. если ,,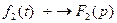 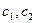- постоянные числа,то

.

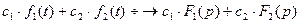ПРИМЕР. Найти изображения функций .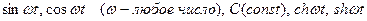

Пользуясь свойством линейности, формулой (1.3) 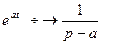находим:

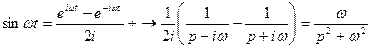
Т.е. 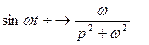(1.5)

Аналогично получаем формулу: 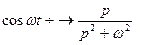. (1.6)

Найдем 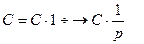,т.е. 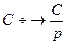. (1.7)

Дале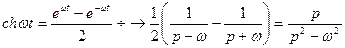е ,т.е.

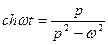. (1.8)

Аналогично . (1.9)

Дата добавления: 2014-01-15