Математическое описание обратной связи

Математическое описание тахогенератора

Дифференциальное уравнение тахогенератора:

U₃ = k₄×W, (5.14)

где k₄= k_тг.

U₂ =U – U₃ (5.15)

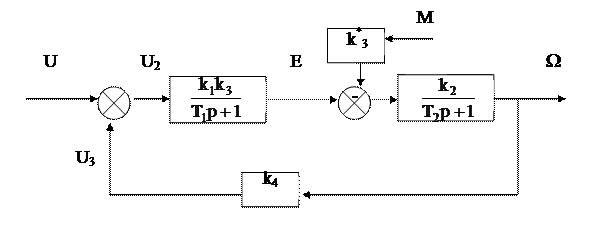Используя вторые формы записи динамических звеньев, получим структурную схему САР в целом (рис.5.4).

Рис.5.4

М U (-) U₂ Е W   U₃ k₄  

В частности, возмущающее воздействие М можно привести ко входу системы (рис.4.31):

Рис.5.5

Приводя структурную схему к единичной обратной связи, получим еще один вид (рис.5.6):

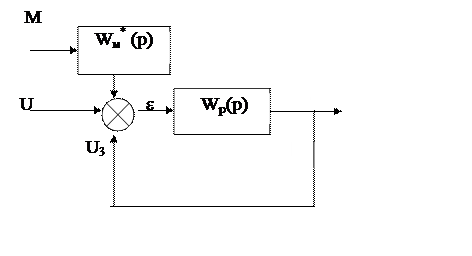
Рис.5.6

Здесь

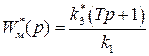- передаточная функция по возмущающему воздействию;

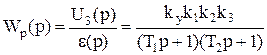- передаточная функция разомкнутой системы.

В соответствии с рис.5.6 соотношение сигналов в изображении по Лапласу имеет вид:

(5.16)

Получим 3 основных вида передаточных функций замкнутой САР:

1. главная передаточная функция замкнутой САР (при М(t)=0)

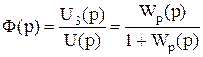; (5.17)

2. передаточная функция замкнутой САР по ошибке (при М(t)=0)

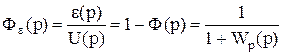; (5.18)

3. передаточная функция замкнутой САР по возмущающему воздействию.

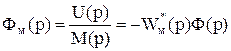. (5.19)

5.2. Частотные характеристики замкнутых САР

В соответствии с выражением (5.17) можно записать частотную передаточную функцию замкнутой системы в виде:

. (5.20)

Тогда АФЧХ можно представить в виде:

, (5.21)

.

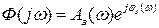Согласно (5.21) запишем:

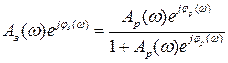. (5.22)

Выражение (5.22) может быть преобразовано к виду:

. (5.23)

Подставив в (5.23)

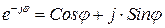(5.24)

и приравняв отдельно вещественные и мнимые части, имеем два равенства:

(5.25)

Сложив квадраты выражений (5.25) и поделив одно на другое, получим выражения для АФЧХ замкнутой системы:

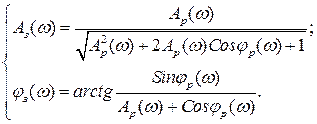(5.26)

На практике для упрощения определения А_з(ω) и φ_з(ω) используют номограммы замыкания, отвечающие зависимостям (5.26).

Таким образом, по точкам строятся частотные характеристики замкнутых САР. Существует и другое представление частотных характеристик замкнутой САР:

(5.27)

где Р(ω), Q(ω) – вещественная и мнимая частотные характеристики замкнутой системы.

Представив АФЧХ разомкнутой САР в виде зависимости:

(5.28)

И подставив (5.28) в (5.20), получим зависимости, определяющие вещественную и мнимую частотные характеристики:

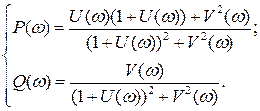(5.29)

Вещественная и мнимая частотные характеристики строятся с помощью специальных круговых диаграмм, построенных на плоскости W(jω) c координатами U и V. Вещественная характеристика является четной функцией о частоты, мнимая – нечетной функцией от частоты.

Кроме того, вещественную и мнимую частотные характеристики можно определить и по заданным АЧХ разомкнутой системы. Для этого подставим:

в (5.20) и получим:

(5.30)

откуда вещественная и мнимая частотные характеристики:

(5.31)

Аналогичным путем строятся частотные характеристики замкнутой САР по возмущающему воздействию, для чего используются соответствующие передаточные функции замкнутой системы.

Дата добавления: 2014-01-15