
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математический аппарат исследования дискретных систем
|
|
|
|
Структура и классификация импульсных систем
Характерная особенность импульсных систем заключается в том, что по крайней мере одна из координат (переменных) в них подвергается квантованию (прерыванию) по времени [18]. Эти квантованные по времени величины при помощи импульсной модуляции преобразуются в последовательность импульсов, которые воздействуют на непрерывную часть системы. Процесс квантования и импульсной модуляции осуществляется импульсным элементом.
Таким образом, импульсная система состоит из импульсного элемента (ИЭ) и непрерывной части (НЧ), составленной из типовых динамических звеньев (рис. 1.1).

Рис. 1.1. Функциональная схема импульсной системы:
ИЭ - импульсный элемент; НЧ - непрерывная часть
В импульсной системе импульсный элемент преобразует непрерывно изменяющуюся величину в последовательность модулированных импульсов (рис. 1.2).

Рис. 1.2.Временные диаграммы изменения сигналов на входе x и
выходе x* импульсного элемента
Процесс импульсной модуляции состоит в изменении по определенному временному закону какого-либо параметра периодически повторяющихся импульсов. Основными параметрами импульсной последовательности (рис. 1.2) являются:
1) высота или амплитуда импульса А;
2) длительность или ширина импульса Тимп ;
3) период повторения (дискретности) или период квантования импульсов Т.
Расстояние между импульсами определяется их временным положением, т.е. частотой повторения (дискретности) или частотой квантования w0 = 2p/Т. Величина, определяющая закон модуляции, называется модулирующей величиной.
В зависимости от того, какой из параметров последовательности импульсов изменяется по закону изменения модулирующей величины, различают следующие виды импульсной модуляции:
1) амплитудно-импульсную модуляцию - АИМ (амплитуда импульса пропорциональна входному сигналу: A = f(x) при T = const, Тимп = const);
2) широтно-импульсную модуляцию - ШИМ (длительность импульса пропорциональна входному сигналу: Тимп = f(x) при A = const, T = const);
3) временную импульсную модуляцию - ВИМ, включающую в себя:
а) фазо-импульсную модуляцию - ФИМ (фаза, т.е. временной сдвиг импульса относительно начала периода дискретности T, пропорциональна входному сигналу: j = f(x) при A = const, T = const, Тимп = const);
б) частотно-импульсную модуляцию - ЧИМ (частота дискретности пропорциональна входному сигналу: w0 = f(x) при A = const, Тимп = const).
Кроме того, различают два рода импульсной модуляции.
Если параметры последовательности импульсов изменяются в зависимости от значений модулирующей величины в фиксированные равноотстоящие друг от друга моменты времени, то такой вид модуляции называется импульсной модуляцией первого рода - ИМ I.
Если же параметры последовательности импульсов изменяются в соответствии с текущим значением модулирующей величины, то такой вид модуляции называется импульсной модуляцией второго рода - ИМ II.
Импульсный элемент производит периодическое замыкание системы на время длительности импульса Тимп; в оставшуюся часть периода дискретности импульсная система остается разомкнутой.
Основными параметрами импульсного элемента являются коэффициент передачи kи, период повторения Т (или частота повторения w0 = 2p/Т), длительность Тимп = gТ (или скважность g, 0 £ g £ 1) и форма выходных импульсов w(t). В зависимости от вида и рода импульсной модуляции импульсные элементы подразделяются на амплитудные, широтные и временные импульсные элементы первого и второго рода.
В зависимости от вида и рода импульсного элемента импульсные системы подразделяются на три типа:
1) амплитудные импульсные системы - АИС,
2) широтные импульсные системы - ШИС,
3) временные импульсные системы - ВИС
первого и второго рода.
В зависимости от того, соблюдается или не соблюдается принцип суперпозиции, т.е. равна или не равна реакция импульсной системы на сумму воздействий сумме реакций на каждое из воздействий порознь, импульсные системы подразделяются на линейные и нелинейные.
В линейных импульсных системах параметры импульсного элемента и непрерывной части системы не зависят от внешних воздействий и величин, характеризующих состояние системы. К линейным импульсным системам относятся АИС с линейной непрерывной частью и линейной характеристикой импульсного элемента, равной коэффициенту передачи
 , (1.1)
, (1.1)
где x - значение входной величины в дискретные моменты времени;
A - соответствующая амплитуда импульса.
В нелинейных импульсных системах параметры импульсного элемента или непрерывной части системы зависят от внешнего воздействия или величин, характеризующих состояние системы. К нелинейным импульсным системам относятся ШИС и ВИС, а также АИС с нелинейной характеристикой импульсного элемента или с нелинейной непрерывной частью.
Если в импульсной системе параметры импульсного элемента или непрерывной части изменяются во времени, то такие системы относятся к импульсным системам с переменными параметрами. Последние могут быть как линейными, так и нелинейными.
В дальнейшем будут рассматриваться линейные амплитудные импульсные системы. Для расчета широтных импульсных систем и временных импульсных систем при определенных ограничениях можно использовать методы линейных АИС.
Величины, описывающие поведение автоматических систем, представляют собой функции времени. Математическое исследование дискретных систем существенно упрощается в том случае, когда все величины рассматриваются в дискретные равноотстоящие моменты времени.
Решетчатые функции и разностные уравнения. Решетчатая функция времени x[nT], или в сокращенной записи x[n] - это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени t = nT, где n - целое положительное число 0, 1, 2..., а Т - период дискретности. То есть решетчатая функция представляет собой числовую последовательность:
x[0], x[1T], x[2T], x[3T],..., x[kT],....
Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Операция замены непрерывной функции решетчатой
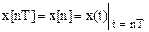 (1.2)
(1.2)
показана на рис. 1.3.
Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками t = nT, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.
Возникает вопрос, при каких условиях возможно точное восстановление квантованной функции. Ответ на него дает теорема Котельникова-Шеннона [5]: непрерывный сигнал x(t), частотный спектр которого ограничен полосой 0 < f < fп, полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию
Т < 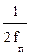 или Т <
или Т < 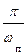 , (1.3)
, (1.3)
где fп[Гц], wп [с-1] - частота пропускания.
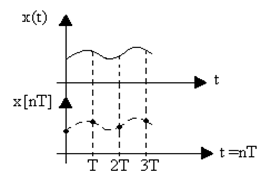
Рис. 1.3.Временные диаграммы изменения непрерывной функции x(t)
и решетчатой функции x[nT]
Смещенная решетчатая функция времени представляет собой числовую последовательность:
x[sT], x[1T+sT], x[2T+sT], x[3T+sT],..., x[kT+sT],...,
образованную в результате выборки значений функции x(t) в точках t = nT+sT оси времени
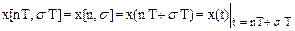 , (1.4)
, (1.4)
где s - постоянное число из интервала 0 £ s < 1.
Параметр s рассматривается в качестве относительного (безразмерного) времени, отсчитываемого от начала очередного (n-го) интервала повторения. Его иногда называют локальным (местным) временем.
Смещенная решетчатая функция x[n,s] для всех возможных значений s позволяет однозначно восстановить “породившую” ее непрерывную функцию x(t).
Своего рода “дискретными аналогами” производных и интегралов непрерывных функций для решетчатых функций являются конечные разности и суммы.
Конечные разности решетчатых функций бывают двух видов: прямые (упреждающие) и обратные (отстающие).
Первая прямая разность
Dx[n,s]=x[n+1,s]-x[n,s] (1.5)
и первая обратная разность
Ñx[n,s]=x[n,s]-x[n-1,s]. (1.6)
Разности произвольного порядка k определяются при помощи рекуррентных соотношений:
Dk x[n,s] = D{Dk-1 x[n,s]}= Dk-1 x[n+1,s] - Dk-1 x[n,s], (1.7)
Ñk x[n,s] = Ñ{Ñk-1 x[n,s]}= Ñk-1 x[n,s] - Ñk-1 x[n-1,s] (1.8)
или формул общего вида
 , (1.9)
, (1.9)
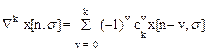 , (1.10)
, (1.10)
где биноминальные коэффициенты (число сочетаний)
 . (1.11)
. (1.11)
Прямая и обратная разности связаны соотношением
Ñk x[n,s] = Dk x[n-k,s]. (1.12)
Соотношения (1.9) и (1.10) показывают, что для вычисления разности k-го порядка в некоторой точке [n,s] требуется знать значение функции x[n,s] в (k+1)-й точке. Для прямой разности этими значениями являются текущее x[n,s] и последующие x[n+1,s], x[n+2,s],..., x[n+k,s] значения; вычисление обратной разности требует знания предыдущих x[n-1,s], x[n-2,s],..., x[n-k,s] значений последовательности x[n,s].
Обратные разности обладают важной особенностью. Если решетчатая функция определена только для положительных значений аргумента, т.е. x[n,s] º 0 при n < 0, то, как следует из (1.10), в точке n = 0 k-я разность
Ñk x[0,s] = x[0,s] (1.13)
для любого целого положительного k.
Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой являются неполная сумма
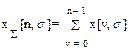 (1.14)
(1.14)
и полная сумма
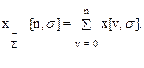 (1.15)
(1.15)
Отличие (1.15) от (1.14) заключается в том, что значение x[n,s] в момент времени t = nT + sT также участвует в формировании результата.
Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности. При использовании прямых разностей неоднородные линейные разностные уравнения m-го порядка имеют вид [2]
b0Dmy[n,s] + b1Dm-1y[n,s] +... + bm-1Dy[n,s] +bmy[n,s] = f[n,s], (1.16)
где f[n,s] - заданная, а y[n,s] - искомая решетчатые функции. При f[n,s] º 0 уравнение (1.16) становится однородным разностным уравнением, решением которого будет y[n,s].
При использовании (1.9) разностное уравнение (1.16) можно записать в другом виде:
a0y[n+m,s] + a1y[n+m-1,s] +... + amy[n,s] = f[n,s]. (1.17)
Коэффициенты этого уравнения определяются
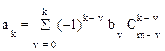 , (1.18)
, (1.18)
где биноминальные коэффициенты (число сочетаний)
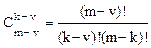 . (1.19)
. (1.19)
При использовании обратных разностей неоднородные линейные разностные уравнения m-го порядка будут
b0Ñmy[n,s] + b1Ñm-1y[n,s] +... + bm-1Ñy[n,s] +bmy[n,s] = f[n,s]. (1.20)
С учетом (1.10) последнее выражение приобретает вид
a0y[n,s] + a1y[n-1,s] +... + amy[n-m,s] = f[n,s]. (1.21)
Коэффициенты этого уравнения определяются
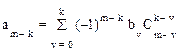 , (1.22)
, (1.22)
где биноминальные коэффициенты (число сочетаний)
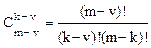 . (1.23)
. (1.23)
Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения y[n+m,s] при n = 0, 1, 2,... для уравнения (1.17) и заданных начальных значений y[0,s], y[1,s],..., y[m-1,s] или значения y[n,s] при n = 0, 1, 2,... для уравнения (1.21) и заданных начальных значений y[n-m,s], y[n-m+1,s],..., y[n-1,s].
Решение уравнения (1.21) при s = 0 представляет собой рекуррентную формулу:
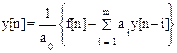 , для n=0, 1, 2,... (1.24)
, для n=0, 1, 2,... (1.24)
при нулевых начальных условиях y[n] º 0 при n < 0. Структурная схема решения приведена на рис. 1.4.
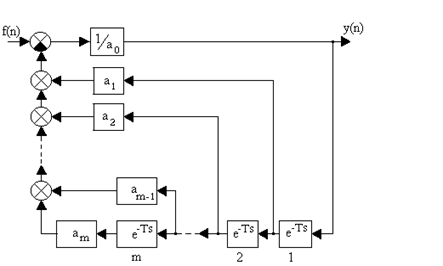 Рис. 1.4.Структурная схема решения разностного уравнения
Рис. 1.4.Структурная схема решения разностного уравнения
Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:
y[n,s] =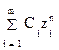 , (1.25)
, (1.25)
где zi - корни характеристического уравнения
a0 zm + a1zm-1 +... + am = 0, (1.26)
Ci - постоянные коэффициенты.
Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w -преобразование, а также частотные методы.
Z - преобразование. Подобно тому, как применение преобразования Лапласа к линейным дифференциальным уравнениям дало возможность получить удобную методику анализа непрерывных систем, для дискретных систем также был разработан ряд специальных преобразований. Из них наибольшее распространение получили дискретное пребразование Лапласа, введенное в 1949 г. Я.З.Цыпкиным [18], и z-преобразование, предложенное в конце 40-х годов Штибицем и Шенноном.
Z-пребразованием решетчатой функции x[nT] называется функция комплексного аргумента z, определяемая выражением
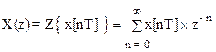 (1.27)
(1.27)
при çzô>R=1/r, где r - радиус сходимости ряда.
Функция x[nT] называется оригиналом, а функция X(z) - изображением или z-пребразованием функции x[nT].
Преобразование, в котором z = esT, было введено Я.З.Цыпкиным под названием “дискретное преобразование Лапласа”.
Z-пребразование (1.27) дает возможность получить из X(z) значение ординат решетчатой функции x[nT] в моменты квантования. Но в системах управления с непрерывными динамическими частями процесс непрерывен и между моментами n = 0, 1, 2... Для нахождения этих ординат необходимо рассмотреть последовательности для других дискретных моментов с тем же интервалом повторения, но смещенных на значение sT: t = (n+s)T при 0 £ s £ 1. Это можно делать с помощью модифицированного z-преобразования.
Модифицированное z-преобразование решетчатой функции x[nT+sT]:
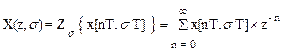 . (1.28)
. (1.28)
Функция X(z,s), определяемая выражением (1.28), называется z-преобразованием непрерывной функции времени x(t) и обозначается как
X(z,s) = Zs {x(t)}; (1.29)
z-преобразование функции x(t) можно также представить следующим образом:
X(z,s) = Zs {X(s)}, (1.30)
где X(s) - преобразование Лапласа от x(t). В этом случае подразумевается, что преобразованию подвергается функция времени и запись (1.30) носит чисто формальный характер.
Т а б л и ц а 1. 1
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 963; Нарушение авторских прав?; Мы поможем в написании вашей работы!