
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Z - преобразования функций времени
|
|
|
|
| x(t) | X(s) | x[nT] | X(z) | X(z,s) |
| d(t) | d[nT] | - | ||
| 1(t) | 1/s | 1[nT] | z/(z-1) | z/(z-1) |
| t | 1/s2 | nT | Tz/(z-1)2 | Tz/(z-1)2+ + +Tsz/(z-1) |
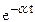
| 1/(s+a) | 
| z/(z-d)
(d=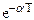 ) )
| ... |
| t2/2! | 1/s3 | (nT)2/2! | 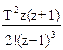
| ... |
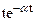
| 1/(s+a)2 | 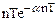
| 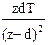 (d=
(d=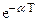 ) )
| ... |
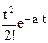
| 1/(s+a)3 | 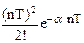
| 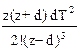 (d=
(d=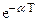 ) )
| ... |
Для нахождения z-изображений решетчатых функций по заданному оригиналу и наоборот имеются специальные таблицы [2, 15, 17], фрагмент такой таблицы приведен выше. Необходимо отметить, что все функции времени, имеющие одинаковые значения в дискретные моменты времени, обладают одинаковыми z-преобразованиями и поэтому связь между функцией времени и ее z-изображением не является взаимно однозначной. Однако, семейство модифицированных z-преобразований решетчатой функции для всех s от 0 до 1 однозначно определяет непрерывную функцию.
Свойства z-преобразования изложены в [2], поэтому ограничимся рассмотрением некоторых из них, которые потребуются в дальнейшем.
1. Свойство линейности. Если F1(z,s)=Zs {f1(t)} и F2(z,s)=Zs {f2(t)}, то
Zs {a1f1(t) + a2f2(t)}= a1 F1(z,s) + a2 F2(z,s). (1.31)
2. Теорема сдвига (смещения). Если Zs {f(t)} = F(z,s) и t - произвольное положительное число, тогда
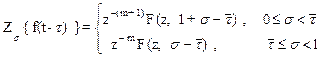 (1.32)
(1.32)
где 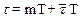 , m - целая,
, m - целая, 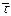 - дробная часть числа t/T;
- дробная часть числа t/T;
если t = mT, тогда
Zs {f(t-mT)}=z-mF(z,s). (1.33)
3. Изображение обратных разностей
Z{Ñkf[nT]}= (1 - z-1)kF(z). (1.34)
4. Изображение конечных сумм:
полных 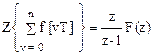 , (1.35)
, (1.35)
неполных  . (1.36)
. (1.36)
5. Предельные значения. Если дискретные значения функции в установившемся режиме существуют, то они могут быть найдены путем следующего предельного перехода:
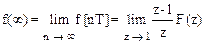 , (1.37)
, (1.37)
начальное значение функции оригинала:
 . (1.38)
. (1.38)
6. Свертка функций. Если F1(z) = Z{f1(t)} и F2(z) = Z{f2(t)}, то
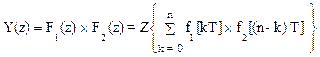 (1.39)
(1.39)
и
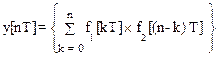 (1.40)
(1.40)
7. Формула обращения. Дискретные значения функции по ее z-преобразованию определяют следующим контурным интегралом:
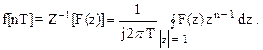 (1.41)
(1.41)
8. Изображение разностных уравнений. Пусть разностное уравнение, связывающее выходную координату y[nT] импульсной системы с ее входным воздействием f[nT], имеет следующий вид:
a0y[n]+a1y[n-1]+...+amy[n- m ] = b0f[n]+b1f[n-1]+...+b l f[n- l ], (1.42)
при m ³ l и y[n] º 0, f[n] º 0 для всех n < 0.
Подвергнув исходное уравнение z-преобразованию, получим
a0Y(z)+a1 z-1Y(z)+...+am z- m Y(z) = b0F(z)+b1 z-1F(z)+...+b l z- l F(z),
которое можно переписать в виде
A(z)Y(z)=B(z)F(z), (1.43)
где полиномы
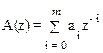 и
и 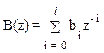 . (1.44)
. (1.44)
Из (1.43) находим изображение выходной координаты
Y(z)=W(z)F(z), (1.45)
где  . (1.46)
. (1.46)
По аналогии с определением передаточной функции непрерывных систем выражение W(z) называется дискретной передаточной функцией импульсной системы.
Данная запись отличается от передаточной функции для непрерывных систем тем, что переменная z в полиномах имеет отрицательные степени. Для того, чтобы была полная аналогия с передаточными функциями непрерывных систем, степень переменной z делают положительной путем домножения числителя и знаменателя выражения (1.46) на zm. Тогда получим формулу, которая полностью аналогична записи для непрерывной функции
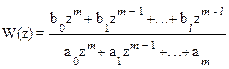 . (1.47)
. (1.47)
Задача получения разностного уравнения по дискретной передаточной функции решается в обратной последовательности.
Пример. Написать разностное уравнение, связывающие выходную координату у[nT] и входное воздействие f[nT] импульсной системы, заданной передаточной функцией
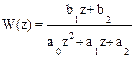 .
.
Решение. Домножим числитель и знаменатель W(z) на z-2. В результате получим
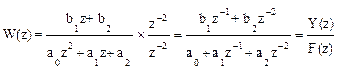 .
.
На основании последнего выражения разностное уравнение будет
a0y[n] + a1y[n-1] + a2y[n-2] = b1f[n-1] + b2f[n-2].
Его решение при нулевых начальных условиях y[n] º 0, f[n] º 0 для всех n < 0:
y[n] = [1/a0]´{b1f[n-1] + b2f[n-2] - a1y[n-1] - a2y[n-2]}.
Полученному решению соответствует структурная схема, приведенная на рис. 1.5.
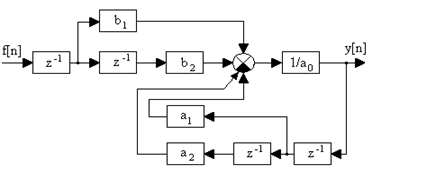
Рис. 1.5. Структурная схема импульсной системы
Комплексный спектр решетчатой функции времени. Комплексный спектр решетчатой функции времени f[n,s] представляет собой комплексную функцию вещественного переменного w, определяемую следующим выражением:
 при -¥ < w < ¥. (1.48)
при -¥ < w < ¥. (1.48)
Таким образом, для получения комплексного спектра необходимо в изображении решетчатой функции произвести замену z = ejwT, откуда следует, что функция z является периодической функцией w с периодом, равным 2p/T. По этой причине комплексный спектр решетчатой функции также является периодической функцией w того же самого периода:
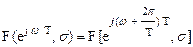 (1.49)
(1.49)
и, следовательно, может рассматриваться на любом интервале значений w, длина которого равна 2p/T. В качестве такого интервала принят интервал
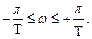 (1.50)
(1.50)
Подобно любой комплексной функции спектр (1.48) может быть представлен в показательной или алгебраической форме записи:
F(ejwT,s) = А(w, s)´ejy(w, s) = U(w, s) + jV(w, s), (1.51)
где A(w, s), y(w, s), U(w, s), V(w, s) называются соответственно амплитудным, фазовым, вещественным и мнимым спектрами решетчатой функции f[n,s]. При фиксированном значении w спектр (1.51) изображается вектором в плоскости (U, jV); при изменении w от -p/T до +p/T, конец вектора F(ejwT,s) прочерчивает некоторую кривую, которая является графическим изображением спектра.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 791; Нарушение авторских прав?; Мы поможем в написании вашей работы!