Виды равновесия твердого тела

Условия равновесия системы тел

Для равновесия1 тела человека (системы тел) необходимо, чтобы главный вектор и главный момент внешних сил были равны нулю, а все внутренние силы обеспечивали сохранение позы (формы системы).

Если главный вектор и главный момент равны нулю, тело не сдви­нется и не повернется, его линейное и угловое ускорения равны нулю. Для системы, тел эти условия также необходимы, но уже недоста­точны. Равновесие тела человека как системы тел требует еще сохра­нения позы тела. Когда мышцы достаточно сильны и человек умеет использовать их силу, он удержится в очень трудном положении. А ме­нее сильному человеку такой позы не удержать, хотя по расположе­нию и величине внешних сил равновесие возможно. У разных людей существуют свои предельные позы, которые они еще в состоянии со­хранять.

Вид равновесия твердого тела определяется по действию силы тяжести в случае сколь угодно малого отклонения: а) безразлич­ное равновесие — действие силы тяжести не изменяется; б) ус­тойчивое — оно всегда возвращает тело в прежнее положение (возникает момент устойчивости); в) неустойчивое — действие силы тяжести всегда вызывает опрокидывание тела (возникает момент опрокидывания); г) ограниченно-устойчивое — до потен­циального барьера положение тела восстанавливается (возникает момент устойчивости), после него тело опрокидывается (возникает момент опрокидывания).

В механике твердого тела различают три вида равновесия: безраз­личное, устойчивое и неустойчивое. Эти виды различаются по поведе­нию тела, незначительно отклоняемого от уравновешенного положе­ния. Когда тело человека полностью сохраняет позу («отвердение»), к нему применимы законы равновесия твердого тела.

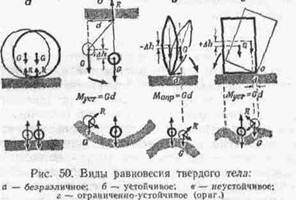
Безразличное равновесие характерно тем, что при любых отклоне­ниях сохраняется равновесие. Шар, цилиндр, круговой конус на го­ризонтальной плоскости (нижняя опора) можно повернуть как угодно, и они останутся в покое. Линия действия силы тяжести (G) в таком теле (или, как говорят, короче линия тяжести) всегда проходит через точку опоры, совпадает с линией действия силы опорной реакции (R); они уравновешивают друг друга. В спортивной технике безразличного равновесия ни на суше, ни в воде практически не встречается.

Устойчивое равновесие характерно возвратом в прежнее положение при любом отклонении. Оно устойчиво при сколь угодно малом от­клонении по двум причинам; а) центр тяжести тела под­нимается выше (Dh), создается запас потенциальной энергии в поле земного тяготения; б) линия тяжести (G) не про­ходит через опору, появляется плечо силы тяжести (d) и возникает момент силы тяжести (момент устойчивости М уст=Gd), возвращающий тело (с уменьшением потенциальной энергии) в прежнее положение. Такое равновесие встречается у человека при верхней опоре. Например, гимнаст в висе на кольцах; рука, свободно вися­щая в плечевом суставе. Сила тяжести тела сама возвращает тело в прежнее положение.

Неустойчивое равновесие характерно тем, что сколь угодно малое отклонение вызывает еще большее отклонение и тело само в прежнее положение вернуться не может. Таково положение при нижней опоре, когда тело имеет точку или линию (ребро тела) опоры. При отклонении тела: а) центр тяжести опускается ниже (—Dh), убывает потенциальная энергия в поле земного тяготения; б) линия тяжести (G) с отклонением тела удаляется от точки опоры, увеличиваются плечо (d) и момент силы тяжести (момент опрокидывания М_опр. =Gd ); он все дальше отклоняет тело от прежнего положения. Неустойчивое равновесие в природе практически почти не осуществимо.

В физических упражнениях чаще всего встречается еще один вид равновесия, когда имеется площадь опоры, расположенная внизу (нижняя опора). При незначительном от­клонении тела центр его тяжести поднимается (+Dh) и появляется момент устойчивости (M_уст=Gd). Налицо признаки устойчивого равно­весия; момент силы тяжести тела вернет его в прежнее положение. Но это продолжается лишь при отклонении до определенных границ, пока линия тяжести не дойдет до края площади опоры. В этом положе­нии уже возникают условия неустойчивого равновесия: при дальней­шем отклонении тело опрокидывается; при малейшем отклонении в обратную сторону — возвращается в прежнее положение. Границе площади опоры соответствует вершина «потенциального барьера» (максимум потенциальной энергии). В пределах между противополож­ными барьерами («потенциальная яма») во всех направлениях осуществ­ляется ограниченно-устойчивое равновесие.

2.4. Устойчивость твердого тела и системы тел

Устойчивость объекта характеризуется его способностью, про­тиводействуя нарушению равновесия, сохранять положение. Различают статические показатели устойчивости как способность сопротивляться нарушению равновесия и динамические как спо­собность восстановить равновесие.

Статическим показателем устойчивости твердого тела служит (в ограниченно-устойчивом равновесии) коэффи­циент устойчивости. На рис. 51, а опрокидывающий момент создается опрокидывающей силой (F_опр), приложенной на плече (h) относи­тельно линии опрокидывания (О), вокруг которой происходит отклоне­ние тела. Момент устойчивости относительно той же линии опрокиды­вания возникает с начала приложения силы F_опр. Наибольшим он становится в начале опрокидывания (предельный момент устойчиво­сти), далее плечо силы тяжести G уменьшается и момент устойчивости уменьшается до нуля (в граничном положении — ОЦТ над линией опрокидывания).

а — коэффициент устойчивости тела; б, в — угол устойчивости (a};г — ста­тическая и динамическая устойчивость системы тел; д — поверхность опоры (пунктир) и площадь эффективной опоры (заштрихована) (ориг.)

Коэффициент устойчивости равен отношению предельного момента устойчивости к моменту опрокидывающему. Когда коэффициент устой­чивости покоящегося тела равен единице и больше нее, опрокидывания нет. Если же он меньше единицы, равновесие не может быть сохра­нено.

Однако сопротивление только этих двух механических факторов (двух моментов сил) для системы тел, если она может изменять конфи­гурацию, не исчерпывает действительной картины. Предположим, что сопротивляющийся борец (рис. 51, г), согнув ноги, опустит строго вертикально центр тяжести своего тела. От этого ни сила тяжести его тела, ни ее плечо, а значит, и момент устойчивости не изменятся. Но понизится точка приложения F_onp плечо этой силы уменьшится, меньше станет ее момент. Таким способом борец может увеличить коэф­фициент устойчивости своего тела путем уменьшения опрокидывающего момента. Отклонив назад тело, он не изменит опрокидывающий момент, но увеличит плечо силы тяжести своего тела и момент устойчивости. Здесь он тоже выиграет в статической устойчивости. Борец, напрягая мышцы и упираясь в ковер, создает еще внешнюю горизонтальную силу (силу трения), направленную в его сторону, уменьшая этим дей­ствие опрокидывающей тяги. Последнее зависит также от готовности мышц борца противодействовать внезапному ее приложению. Обман­ными действиями можно резко ухудшить их готовность и малой тягой вызвать опрокидывание. Самое существенное для биомеханической системы не в пассивном использовании силы тяжести тела, а в активных мышечных тягах, сохраняющих и изменяющих позу тела. В системе тел каждое звено должно быть в равновесии, сохраняя ее конфигура­цию (позу тела человека).

Следовательно, коэффициент устойчивости тела и зафиксированной системы тел характеризует статическую устойчивость как способность сопротив­ляться нарушению равновесия. У человека при определении устойчивости всегда надо еще учитывать активное противо­действие мышечных тяг и готовность к сопротивлению.

Динамическим показателем устойчивости твердого тела служит угол устойчивости. Это угол, образованный ли­нией действия силы тяжести и прямой, соединяющей центр тяжести с соответствующим краем площади опоры (см. рис. 51, б, в). Станем отклонять тело, пока линия тяжести не дойдет до границы площади опоры (граничное положение тела — вершина потенциального барьера). У тела, поставленного стоймя (рис. 51, б), база устойчивости (/i) меньше, чем у того же тела, лежащего плашмя (/2) (см. рис. 51, в). Значит, линия тяжести ближе к границе, за которой начнется опроки­дывание. Центр тяжести надо поднять для опрокидывания в первом случае на меньшую высоту (Dh₁), чем во втором (Dh₂) Угол устойчи­вости в первом случае (a₁) явно меньше, чем во втором (a₂).

Физический смысл угла устойчивости состоит в том, что он равен углу поворота (<р), на который надо повернуть тело для начала его опрокидывания. Угол устойчивости показывает, в каких пределах еще восстанавливается равновесие. Он характеризует степень динамиче­ской устойчивости: если угол больше, то и устойчивость больше. Этот показатель удобен для сравнения степени устойчивости одного тела в разных направлениях (если площадь опоры не круг и линия силы тя­жести не проходит через его центр).

Сумма двух углов устойчивости в одной плоскости рассматривается как угол равновесия в этой плоскости. Он характеризует запас устой­чивости в данной плоскости, т. е. определяет размах перемещений центра тяжести до возможного опрокидывания в ту или другую сто­рону (например, у слаломиста при спуске на лыжах, гимнастки на бревне, борца в стойке).

В случае равновесия биомеханической системы дляприменения динамических показателей устойчивости нужно учесть существенные уточнения.

Во-первых, площадь эффективной опоры человека не всегда совпа­дает с поверхностью опоры. У человека, как и у твердого тела, поверх­ность опоры ограничена линиями, соединяющими крайние точки опоры (или внешние края нескольких площадей опоры) (см. рис. 51, д). Но у человека часто граница площади эффективной опоры расположена внутри контура опоры, так как мягкие ткани (стопа босиком) или сла­бые звенья (концевые фаланги пальцев в стойке на руках на полу) не могут уравновесить нагрузку. Поэтому линия опрокидывания сме­щается кнутри от края опорной поверхности, площадь эффек­тивной опоры меньше площади опорной по­верхности.

Во-вторых, человек никогда не отклоняется всем телом относительно линии опрокидывания (как кубик), а перемещается относительно осей каких-либо суставов, не сохраняя полностью позы (например, при положении стоя —движения в голеностопных суставах).

В-третьих, при приближении к граничному положению нередко ста­новится трудно сохранить позу и наступает не просто опрокидывание «отвердевшего тела» вокруг линии опрокидывания, а изменение позы с падением. Это существенно отличается от отклонения и опрокиды­вания твердого тела вокруг грани опрокидывания (кантование).

Таким образом, углы устойчивости в ограниченно-устой­чивом равновесии характеризуют динамическую устой­чивость как способность восстановить рав­новесие. При определении устойчивости тела человека необходимо также учитывать границы площади эффективной опоры, надежность сохранения позы до гранич­ного положения тела и реальную линию опрокидывания.

В физических упражнениях часто встречается удерживающая связь (жесткая). Тогда условия сохранения равновесия требуют учета двусторонней связи путем рассмотрения соответствующих реактивных сил, вызванных такой связью.

3.СОХРАНЕНИЕ И ВОССТАНОВЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА ЧЕЛОВЕКА

Человек может не только сохранять равновесие, но и восстанавли­вать его в случаях нарушения. Отличие равновесия биомеханических систем от равновесия твердых физических тел заключается не в наличии особых законов механики для живых систем, а в более сложном их использовании благодаря особенностям живых систем.

Дата добавления: 2014-01-15