
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие положения. Одними из основных фильтрационных характеристик являются объемный расход флюида (Q) вектор скорости фильтрации
|
|
|
|
Лекция № 6
Одними из основных фильтрационных характеристик являются объемный расход флюида (Q) вектор скорости фильтрации 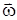 .
.
Объемный расход-это объем флюида, проходящего в единицу времени через произвольную площадку DS.
Определим скорость фильтрации как вектор, проекция которого на любое направление, равна отношению объемного расхода (потока) флюида к площадке DS, перпендикулярной к этому направлению.
|
Поэтому, различают еще одну скоростную характеристику – среднюю скорость фильтрации. Она получается путем деления расхода не на всю площадь, а на суммарную площадь активных пор:
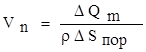 ,
,
отсюда 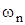 = mVn, где m – пористость. Поскольку m<1, следует, что Vn>
= mVn, где m – пористость. Поскольку m<1, следует, что Vn>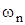 .
.
Основное соотношение теории фильтрации - закон фильтрации. Закон устанавливает связь между скоростью фильтрации и тем полем давления, которое вызывает фильтрационное течение.
Первые экспериментальные наблюдения за движением воды в трубах, заполненных песком, провели французские инженеры Дарси и Дюпюи. Этими работами положено начало теории фильтрации. Именем Дарси назван линейный закон фильтрации, который он установил, создавая первую совершенную систему водоснабжения в Европе.
В результате тщательно проверенных экспериментов установлена, получившая широкую известность, экспериментальная формула, имеющая несколько форм (вариантов) записи:
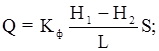
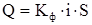 ;
; 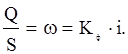
где: Кф – коэффициент, названный коэффициентом фильтрации, зависящий от структуры пористости и свойств флюида; Н1 и Н2 – напоры воды на верхнем и нижнем сечениях трубы; Q - объемный расход жидкости; i – градиент напора; L - длина и S - площадь сечения трубы с песком (рис. 6.2).
Последняя формула читается так: скорость фильтрации пропорциональна градиенту напора.
|
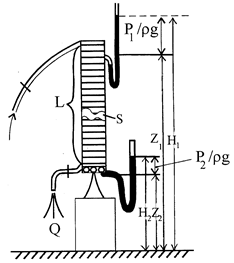
Рис.6.2
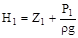 , rgH1 = P*1 = rgZ1+P1; , rgH1 = P*1 = rgZ1+P1;
| 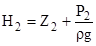 rgH2 = P*2 = rgZ2+P2 rgH2 = P*2 = rgZ2+P2
|
где: P*1 и P*2 – приведенные давления, обычно равные соответственно P1 и P2 при малых rgZ.
Коэффициент фильтрации Кф используют обычно в гидротехнических расчетах, где приходится иметь дело с одной жидкостью - водой.
При исследовании фильтрации сложных флюидов (смеси нефти, газа и воды) необходимо разделить влияние свойств пористой среды и флюида, заключенных в Кф. Поэтому используют формулу Дарси в несколько ином виде, где вместо Кф фигурирует k - коэффициент проницаемости, зависящий только от структуры пористой среды, а свойства жидкости задаются динамически вязкостью (m) и плотностью (r)
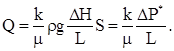
или вторую форму уравнения Дарси,
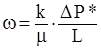 ,
,
где: m - коэффициент вязкости; Р* = rgH = Р+rgz - приведенное давление, совпадающее с истинным при z = 0; k - коэффициент проницаемости, который не зависит от свойств жидкости и характеризует пористую среду. Он имеет размеренность площади [k]си = м2. При этом проницаемость большинства горных пород выражается весьма малыми числами. Так, например: проницаемость крупнозернистых песчаников составляет 10-12-10-13 м2 (1-0,1 мкмм2); проницаемость плотных песчаников 10-14-10-15м2. [k]си = м2 – очень крупная единица измерения проницаемости. Распространена единица Дарси 1D = 1.02×10-12 м2. Размерность [Кф]си - м/с Размерность [m]си=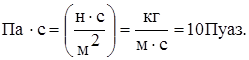
Далее будем считать, что приведенное давление совпадает с истинным, тогда 1-я и 2-я формулы уравнения Дарси запишутся:
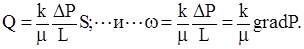
Скорость фильтрации прямо пропорциональна проницаемости и градиенту давления и обратно пропорциональна вязкости жидкости.
Закон Дарси можно записать еще в 3-ей форме выражения
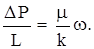
Закон читается так: потеря давления при фильтрации идет на преодоление сил вязкого трения и пропорциональна скорости фильтрации w.
В лабораторных условиях коэффициент фильтрации Кф или проницаемости k определяют при помощи пермеаметра – прибора, похожего на установку Дарси (рис. 6.3).
Зная параметры установки (S, L), поддерживая постоянный расход Q и измеряя разность напоров DН, вычисляют:
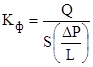 ;
; 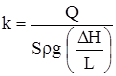 .
.
В природных условиях коэффициент k определяют в результате исследования скважин путем установления зависимости между изменением давления в скважине и ее дебитом.
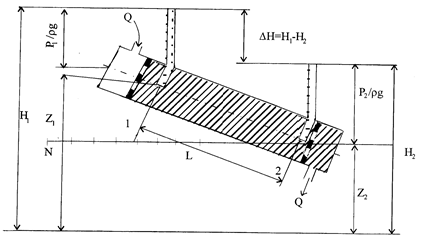
Рис.6.3
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 919; Нарушение авторских прав?; Мы поможем в написании вашей работы!
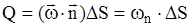 ;
; 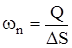 ;
или через массовый расход (Qm):
;
или через массовый расход (Qm):
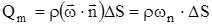 ;
; 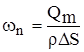 ,
где: Q – объемный расход флюида, м3/с; Qm – массовый расход флюида, к г /с; r – плотность, кг /м3;
,
где: Q – объемный расход флюида, м3/с; Qm – массовый расход флюида, к г /с; r – плотность, кг /м3; 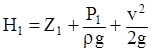 ;
; 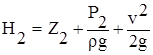 ,
где: Р1 и Р2 – давления замеренные на верхнем и нижнем срезе образца в трубе.
Скорости фильтрации – величины малые, поэтому
,
где: Р1 и Р2 – давления замеренные на верхнем и нижнем срезе образца в трубе.
Скорости фильтрации – величины малые, поэтому 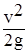 = 0 и поэтому:
= 0 и поэтому: