Лекция № 15

Интерференция скважин.

3.8.1 Общие положения

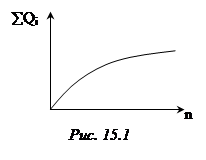Явление интерференции (взаимодействия) скважин заключается в том, что под влиянием пуска, останова или изменения режима работы одной группы скважин, изменяются дебиты и забойные давления других групп скважин, эксплуатирующих этот же пласт. Именно из-за интерференции суммарный дебит нефти по мере ввода новых скважин растет медленнее, чем их число (рис. 15.1).

Введем некоторые новые понятия:

- точечный сток – точка на плоскости пласта, поглощающая жидкость; сток можно рассматривать как гидравлически совершенную скважину бесконечно малого радиуса в пласте единичной мощности (рис. 15.2 (а));

- точечный источник – точка, выделяющая жидкость (модель нагнетательной скважины) (рис. 15.2 (б)).

Найдем потенциал Ф точечного стока на плоскости. Т.к. точечный сток является моделью добывающей скважины и течение вокруг него плоскорадиальное, то скорость фильтрации можно выразить через удельный дебит (дебит скважины на единицу мощности)

,

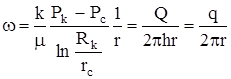где: w - скорость фильтрации; Q- объемный дебит; q = Q/h - удельный дебит жидкости.

Связь потенциала скорости фильтрации с вектором скорости

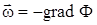, где: ^.

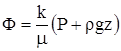Если направление касательной 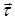к траектории движения совпадает с направлением скорости фильтрации и градиента давления, тогда:

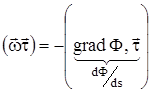или ,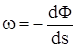

но для плоскорадиального течения .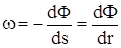

Отсюда 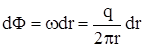и после интегрирования .

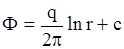Потенциал в точке r = 0 и r = ¥ теряет смысл. Эквипотенциальные линии представляют собой семейство окружностей r = const.

Для точечного источника выражение потенциала аналогичное, но q<0.

Найдем теперь потенциал точки стока не в плоскости, а в пространстве. Рассуждения аналогичные, что и для стока на плоскости, но движение вблизи такого рода стока радиально-сферическое, поэтому

, .

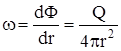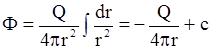Для потенциала точечного источника знак дебита меняется на противоположный.

Модель точечного стока в пространстве будет в дальнейшем использована для решения различных задач притока жидкости к гидравлически совершенным и несовершенным скважинам.

Отметим, что метод стоков и источников находит применение не только для решения задач фильтрации, но также задач теплопроводности, электричества и магнетизма.

Вернемся к вопросам интерференции. Математический смысл метода суперпозиции заключается в том, что если имеется несколько источников фильтрационных потоков от скважин с потенциалами Ф₁(x, y, z), Ф₂ (x, y, z) … Ф_n (x, y, z), каждый из которых удовлетворяет уравнению Лапласа DФ_i = 0, то сумма их 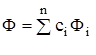- также является его решением. Подбирая с_i можно удовлетворить всем граничным условиям.

Гидродинамический смысл метода суперпозиции состоит в том, что давления (потенциалы) в любой точке пласта, вызванные работой каждой скважины (добывающей и нагнетательной) алгебраически суммируется, а вектор суммарной скорости фильтрации частицы жидкости в данной точке находится как геометрическая сумма векторов скоростей, вызванных работой каждой скважины.

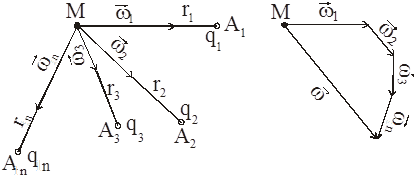
Пусть на неограниченной плоскости расположены n стоков, потенциал каждого из них в точке М равен Ф⁽ⁱ⁾_M, где: i = 1,2….n (рис. 15.3).

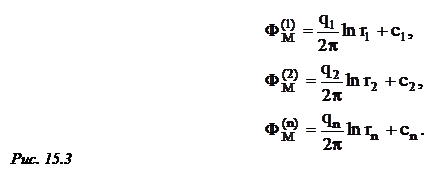
Каждая из функций потенциалов Ф⁽ⁱ⁾_M удовлетворяет уравнению Лапласа, тогда и суммарный потенциал в точке М

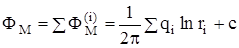, где ,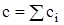

также является его решением. Физически это означает, что фильтрационные потоки накладываются друг на друга. В этом и заключается принцип интерференции. Вектор суммарной скорости фильтрации 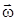в точке М равен геометрической сумме векторов скоростей (рис. 15.3).

,

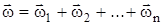где:.

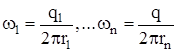Метод суперпозиции можно использовать не только в пластах, имеющих круговой контур питания, или бесконечно больших пластах, но и имеющих контур питания или непроницаемую границу иной формы. В этом случае для выполнения граничных условий приходится вводить фиктивные точечные стоки и источники. При этом решение задач в таких пластах сводится к учету одновременной работы и реальных и фиктивных источников. Метод называется методом отображения стоков и источников.

Рассмотрим, изложенные здесь принципы суперпозиции, при решении некоторых задачах, имеющих практическое применение в разработке нефтегазовых месторождений.

3.8.2. Приток жидкости к группе скважин в пласте с удаленным контуром питания.

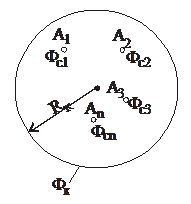Пусть в горизонтальном пласте толщиной h расположена группа скважин А₁, А₂… А_n, c радиусами r_ci, работающими с различными забойными потенциалами Ф_ci:

,

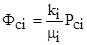где: 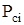- давление на забое скважин.

Рис. 15.4

Так как контур питания достаточно удален от всех скважин, можно приближенно считать, что их расстояния до точек контура одинаковы и

равны R_k (рис. 15.4).

Потенциал в любой точке пласта, в том числе на забое любой скважины (Ф_сi), определяется как сумма потенциалов всех источников:

,

,

………………………………………………………….

.

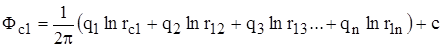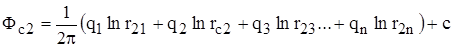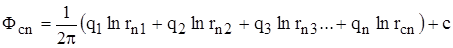Система состоит из n уравнений и содержит n+1 неизвестных (n дебитов и постоянную интегрирования с). Дополнительное уравнение получим, поместив точку М на контур питания:

.

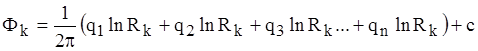Вычитая почленно уравнения системы из последнего уравнения (исключая тем самым с), получим новую систему из n неизвестных относительно q_i:

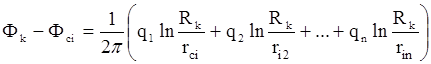, i = 1, 2... n..

На основании этих уравнений можно также определить неизвестные потенциалы по известным дебитам.

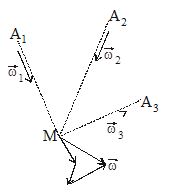
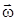Скорость фильтрации в любой точке пласта М определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины (рис.15.5).

; .

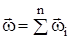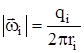Рис. 15.5

3.8.3. Приток жидкости к скважине с прямолинейным контуром питания.

Пусть в полубесконечном пласте на расстоянии a от прямолинейного контура питания с контурным потенциалом Ф_k, работает в точке А одна добывающая скважина забойным потенциалом Ф_с. Требуется найти удельный дебит (q), скорость фильтрации (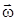) и потенциал (Ф) в любой точке пласта М (рис. 15. 6).

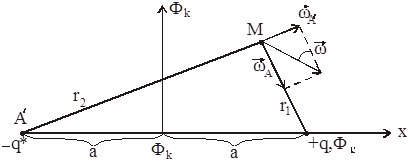
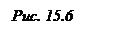
Формула потенциала точечного стока 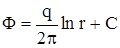справедлива, если скважина расположена в бесконечном пласте или в центре пласта с круговым контуром питания, когда обеспечено плоскорадиальное течение.

Условие постоянства контурного потенциала Ф_k здесь не выполняется из-за конечного расстояния до контура питания. Для решения задачи используем рассмотренный метод отображения стоков и источников.

Влияние прямолинейного контура приводит к появлению фиктивного зеркального источника – q^* в точке А ^/ на расстоянии aот прямолинейного контура питания.

Потенциал в любой точке М пласта определяется как сумма потенциалов от двух источников:

,

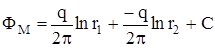где: q – действительный сток; -q – фиктивный источник.

Потенциал на контуре получим, полагая r₁ = r₂:

Ф_k = С = const.

Постоянство потенциала свидетельствует о корректности применяемого метода. Для вычисления дебита скважины найдем ее забойный потенциал, переместив точку М на забой скважины, т.е. положив r₁ = r_с и r₂ = 2a:

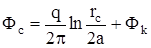, отсюда .

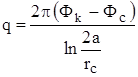Формула совпала с формулой Дюпюи при условии R_к = 2а.

В реальных условиях форма контура питания неизвестна, но вероятней всего она располагается между окружностью радиуса а и прямой, которой соответствует R_к =2а (рис. 15.7).

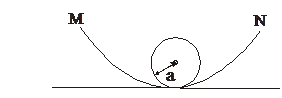
Поэтому удельный дебит q определяется из неравенства:

.

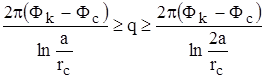Уравнение линии равного потенциала можно поучить из выражения потенциала в любой точке М (х, у) пласта

.

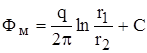Положив этот потенциал постоянной величине и представив радиусы-векторы r₁ и r₂ в координатой форме, найдем уравнение линии равного потенциала, проходящей через точку М:

.

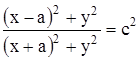Это уравнение можно преобразовать к уравнению семейства окружностей с центрами, лежащими на оси x:

.

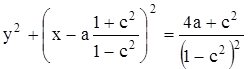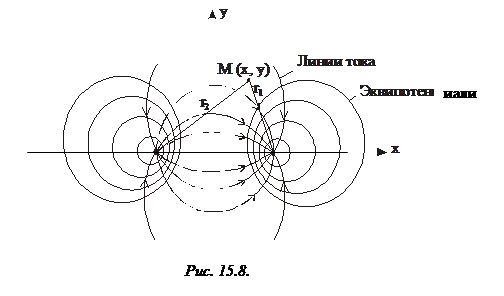
Аналогично можно показать, что семейство линий тока также будет представлять окружности, но с центрами на оси у. Окружности будут перпендикулярными к эквипотенциалям и проходить через сток и фиктивный источник (рис.15.8).

3.8.4. Приток жидкости к скважине, расположенной вблизи непроницаемой прямолинейной границы.

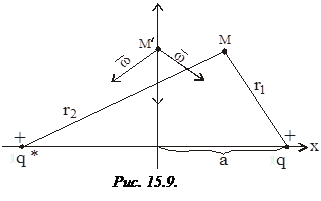Такой модели соответствует геологическая ситуация, когда добывающая скважина расположена возле сброса или границы выклинивания продуктивного пласта. С помощью метода отображения стоков и источников скважину-сток зеркально отображают относительно непроницаемой границы, в скважину-сток такого же дебита и знака (рис. 15.9). Справедливость такого отображения подтверждается тем, что вектор скорости фильтрации при r₁ = r₂ будет направлен вдоль границы. Это означает, что граница является линией тока и фильтрация через нее отсутствует. Дебит скважины в такой модели можно определить из систем 2-х уравнений для модели с удаленным контуром питания:

,

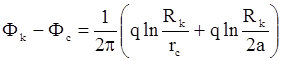где: 2а = r₁₂, отсюда

.

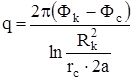Дата добавления: 2014-01-15