Лекция №16

3.8.5. Приток жидкости к скважине, эксцентрично расположенной в круговом пласте.

Пусть в плоском пласте мощностью h с круговым контуром питания радиуса R_к, на контуре которого поддерживается постоянный потенциал Ф_k, на расстоянии d от центра в т. A расположена скважина-сток в точке А, с забойным потенциалом Ф_с. Требуется определить дебит скважины и потенциал Ф_M (х, у) в любой точке пласта M (рис. 16.1).

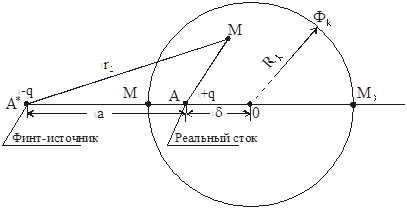
Рис. 16.1

Воспользуемся методом отображения стока в круге радиусом R_k. В этом случае отображением стока +q в т. A будет источник –q в т. A^*, расположенной на продолжении ОА на расстоянии «а» от т. А. Найдем это расстояние из условия постоянства Ф_k на круге, в частности в 2-х его точках М₁ и М₂:

;

;

; .

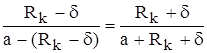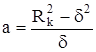Для того, чтобы определить дебит скважины в т. А запишем выражение ее забойного потенциала:

.

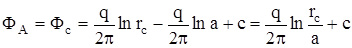Чтобы избавиться от константы вычтем полученное выражение забойного потенциала из выражения контурного потенциала в т. M₁:

.

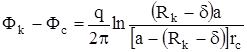Подставляя сюда значение а, получим:

,

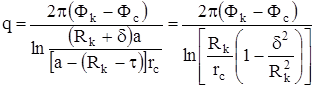при d = 0 формула переходит в формулу Дюпюи.

Выражение потенциала в любой точке М:

.

Вычитая из этого выражения уравнение Ф_М1=Ф_k и учитывая выражение для «а», получим:

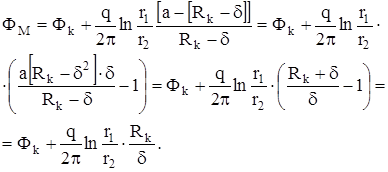
3.8.6. Приток жидкости бесконечным цепочкам и кольцевым батареям скважин.

На примере притока жидкости к нескольким рядам (плоскопараллельный поток) или кольцеобразным батареям скважин (плоскорадиальный поток) ознакомимся с широко применяемым на практике при проектировании разработки месторождений методом эквивалентных фильтрационных сопротивлений. Метод предложен Ю.А. Борисовым и основан на аналогии движения жидкости в пористой среде и электрического тока в проводниках.

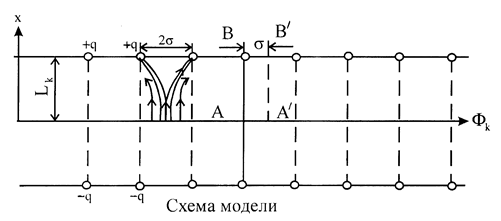
Рис. 16.2

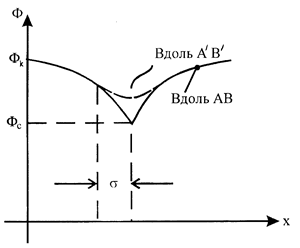Модель (L, Ф_к, Ф_с) – цепочка скважин на расстоянии 2s друг от друга и на расстоянии L от прямолинейного контура питания.

Рис. 16.3

При этом удельный дебит каждой скважины по методу отображения равен:

,

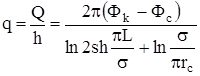где: 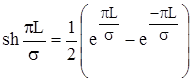, при L >> s, величина 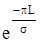очевидно малая и

,

,

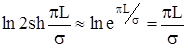где: 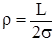- внешнее фильтрационное сопротивление; а 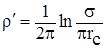- внутреннее фильтрационное сопротивление.

Введение фильтрационных сопротивлений r и r^/ позволяет записать удельный дебит в форме аналогичной закону Ома:

,

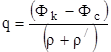где: q ® J; (Ф_k - Ф_c) ® U_k - U_c.

Суммарный дебит всей прямолинейной цепочки из n скважин:

,

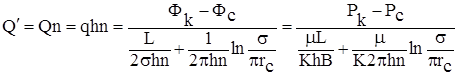где: 2sn = В – длина цепочки скважин.

Аналогично суммарный дебит круговой батареи из n скважин определяется выражением

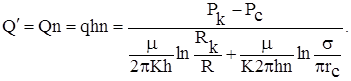, где: R_k-радиус контура питания; R-радиус круговой батареи; s- половина расстояния между скважинами на контуре.

Введем аналогию между гидродинамическими характеристиками фильтрационного потока и характеристиками электрического тока: Q₁^/® I; (P_k-P_c)®DU; 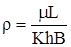- внешнее фильтрационное сопротивление и 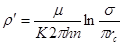- внутреннее фильтрационное сопротивление. Тогда электрогидравлическая схема для одной цепочки (батареи) скважин будет иметь вид (рис. 16.4):

Сопротивление r представляет гидравлическое сопротивление потоку жидкости шириной В на пути L от контура питания до галереи, а r^/ - отражает сопротивление потоку при подходе непосредственно к скважинам в зоне

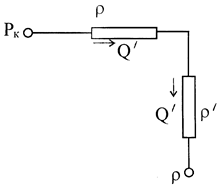
Рис. 16.4

Пусть теперь в полубесконечном пласте с прямолинейным контуром питания работают три параллельных цепочки добывающих скважин с числом n₁, n₂, n₃ соответственно. Скважины в каждой цепочке имеют одинаковые радиусы 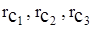и забойные давления Р_С1, Р_С2, Р_С3, а суммарные дебиты цепочек равны, соответственно Q₁^/, Q₂^/, Q₃^/.

Электрогидравлическая схема будет состоять из трех цепочек фильтрационных сопротивлений и будет выглядеть (рис. 16.5):

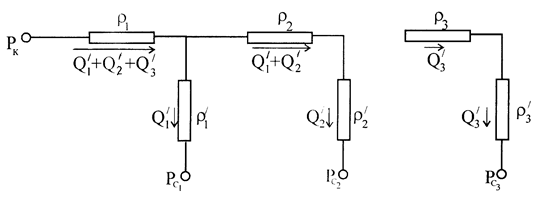
Рис. 16.5

Расчет схемы производится аналогично расчету разветвленных электрических цепей по законам Ома и Кирхгофа. Составляются алгебраические линейные уравнения по числу неизвестных: дебитов Q₁^/, Q₂^/, Q₃^/ (токов), если известны забойные давления (потенциалы), или наоборот.

Внешние сопротивления рассчитываются по формуле

,

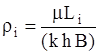где: 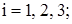L_i – расстояние от контура питания до i-й цепочки.

Внутренние сопротивления будут

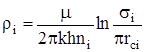, i = 1, 2, 3….

Отметим, что приток жидкости к трем кольцевым батареям скважин с круговым контуром питания рассчитывается по такой же схеме электрических сопротивлений; при этом сохраняются и формулы расчета внутренних фильтрационных сопротивлений, а внешние сопротивления рассчитываются по формуле

, i = 1, 2, 3…..

При расчете фильтрационных сопротивлений следует учитывать, что номера прямолинейных или кольцевых батарей отсчитываются от контура питания. Контур питания первой батареи совпадает с истинным контуром, а каждой последующей, совпадает с положением линии предыдущей батареи (рис. 16.6).

Расстояния L_i для расчета внешних фильтрационных сопротивлений плоскорадиального потока показаны на рисунке 16.6-а, а для расчета ана-

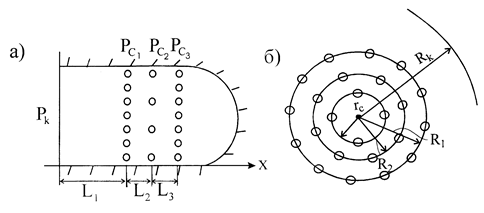
Рис. 16.6

логичных сопротивлений круговых батарей соотношение 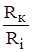будет следующим: для первой батареи 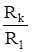, для второй 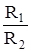, для третьей 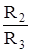и т.д.

Дата добавления: 2014-01-15