Лекция № 17. Приток жидкости к несовершенным скважинам

Приток жидкости к несовершенным скважинам.

Скважина называется гидродинамически совершенной, если она вскрывает пласт на всю его мощность и на этом интервале скважина не обсажена (открыта), так что вскрытая поверхность забоя является фильтрующей.

Скважина называется несовершенной по следующим условиям:

- по степени вскрытия пласта (пласт вскрыт не на всю мощность), при этом ђ = b/h – называется относительным вскрытием пласта, где b – вскрытая мощность;

- по характеру вскрытия; скважина обсажена (или в ней находится специальный фильтр) и она сообщается с пластом через перфорационные отверстия в трубе (цементе) или отверстия в фильтре.

Встречаются скважины с двойным несовершенством. Гидродинамическое несовершенство скважин оценивается коэффициентом d = Q/Q_сов.

Приток жидкости к несовершенной скважине даже в бесконечном горизонтально - однородном пласте перестает быть плоскорадиальным. Строгие математические решения задач притока жидкости к несовершенным скважинам представляют большие трудности. Существует несколько подходов к решению таких задач:

1. Расчетный. Задача о притоке жидкости к несовершенным скважинам по степени вскрытия пласта математически исследовалась М. Маскетом. При этом получена следующая формула для дебита:

,

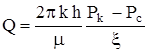где: , .

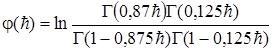Здесь - интеграл 2-го ряда Эйлера (Гамма-функция, для которой имеются таблицы в математическом справочнике).

График j (ђ) имеет вид (рис 17.1).

	Нетрудно видеть, что при ђ = 1 формула Маскета переходит в формулу Дюпюи для плоско-радиального потока.

Рис. 17.1

Иногда для расчета дебитов несовершенных по вскрытию пласта скважин используют формулу И. Козени:

; при ђ = 1 формула переходит в формулу Дюпюи.

Формула Козени удобна тем, что для рассчета не требует справочных данных Гамма-функции.

2. Электрическое моделирование, основанное на электрогидродинамической аналогии фильтрационных процессов.

Ванна заполняется электролитом. В электролит помещается кольцевой электрод, имитирующий контур питания, а в центре его погружается штыревой электрод-скважина на глубину, соответствующую степени вскрытия пласта скважиной. К обоим электродам подается разность потенциалов тока. Возникающий ток является аналогом дебита скважины.

Дебит гидравлически несовершенной скважины подсчитывается по формуле:

,

где: C = с₁+с₂ – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия (с₁) и характеру вскрытия (с₂).

Измеряя разность потенциалов и силу тока, можно подсчитать по закону Ома общее сопротивление, сделать пересчет и определить дополнительные фильтрационные сопротивления.

Такие экспериментальные исследования проведены В.И. Щуровым. Им определены:

с₁ = с₁(а = h D_c, ħ = b/h) и с₂ = с₂ (n D_c, l = l^/ /D_c, α = d^/ /D_c),

где: n – число перфорационных отверстий на метр; D_c – диаметр скважины; l^/ - глубина проникновения перфорационных пуль в породу; d^/ - диаметр отверстий.

Составлены номограммы Щурова для определения с₁ и с₂ , первая из них показана на рис. 17.2.

.

3. И.А. Чарный предложил оценочный метод определения дебита, если величина b вскрытия пласта мала (b << h).

Область движения условно разбивается на две зоны: 1-я зона, где преимущественно плоскопараллельное движение от контура питания до зоны радиуса R₀; 2-я зона, где движение можно считать сферически- радиальным до расстояния R₀ от скважины (рис. 17.3).

Тогда дебит в первой зоне на ее границе со 2-й можно записать через формулу Дюпюи

.

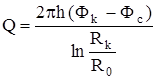Дебит во второй зоне на ее границе с 1-й, учитывая сферически-радиальный характер фильтрации, можно определить по формуле:

Приравнивая эти дебиты, в виду неразрывности потока, и применяя правило преобразования пропорции, получаем формулу обобщенного дебита для скважины, вскрывшей пласт на малую глубину:

,

принимая R₀ = 1,5 h, получаем окончательную формулу:

.

Задачи притока жидкости к скважинам, несовершенным по характеру вскрытия и с двойным несовершенством, еще сложнее.

На практике удобно рассчитывать дебит гидравлически несовершенной скважины также по формуле Дюпюи, но в этом случае в ней фигурирует не истинный радиус скважины, а приведенный:

,

где: 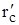- приведенный радиус. Найдем его, приравняв дебиты скважины, выраженные через приведенный радиус и через фильтрационные сопротивления:

.

Приравнивая, получим: , .

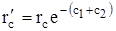Этот прием позволяет рассчитать дебит несовершенных скважин по известной формуле Дюпюи, но с приведенным радиусом.

Иногда гидродинамическое несовершенство учитывается при помощи коэффициента несовершенства d, вычислив который как отношение дебита несовершенной скважины к дебиту совершенной, можно определить коэффициент C=с₁ +с₂, выражающий сумму дополнительных фильтрационных сопротивлений

;

;

.

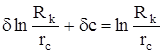3.10. Решение плоских задач фильтрации методом теории комплексного переменного

Дата добавления: 2014-01-15