
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Парабола
|
|
|
|
Вступ.
План.
5. Рівняння площини у просторі (*).
6. Рівняння прямої у просторі (*).
7. Кут між прямою і площиною (*).
8. Окремі випадки завдання площини у просторі (*).
5.1 Рівняння площини у просторі
5.1.1 Загальне рівняння площини
 Нехай задана площина
Нехай задана площина 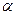 ,
,  - вектор, перпендикулярний (нормальний) до площини
- вектор, перпендикулярний (нормальний) до площини 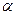 ,
, 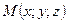 - довільна точка площини,
- довільна точка площини,  - фіксована точка площини.
- фіксована точка площини.

Так як 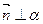 , то
, то 
 Þ
Þ 

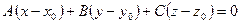 - рівняння площини, що має нормальний вектор.
- рівняння площини, що має нормальний вектор.
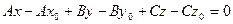
 позначимо
позначимо  , тоді
, тоді
 - рівняння площини в загальному вигляді.
- рівняння площини в загальному вигляді.
Дослідження:
1) 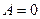 ,
,  - рівняння площини, паралельної осі Ох;
- рівняння площини, паралельної осі Ох;
2)  ,
, 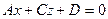 - рівняння площини, паралельної осі Оу;
- рівняння площини, паралельної осі Оу;
3)  ,
,  - рівняння площини, паралельної осі Оz;
- рівняння площини, паралельної осі Оz;
4)  ,
,  - рівняння площини, що проходить через початок
- рівняння площини, що проходить через початок
системи координат;
5) 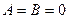 ,
, 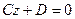 - рівняння площини, паралельної площині ХОУ;
- рівняння площини, паралельної площині ХОУ;
6)  ,
,  - рівняння площини, паралельно площині ХОZ;
- рівняння площини, паралельно площині ХОZ;
7)  ,
, 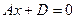 - рівняння площини, паралельно площині УОZ;
- рівняння площини, паралельно площині УОZ;
5.1.2 Рівняння площини у відрізках на осях





позначимо  , тоді
, тоді
 - рівняння площини у відрізках на осях.
- рівняння площини у відрізках на осях.
5.1.3 Рівняння площини, що проходить через три точки
Точки  ,
,  ,
,  - фіксовані точки площини,
- фіксовані точки площини,  - довільна точка площини.
- довільна точка площини.
З цих чотирьох точок утворимо три вектори
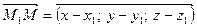

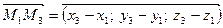
Ці вектори лежать в одній площині, якщо їх змішаний добуток дорівнює нулю.
 - рівняння площини, що
- рівняння площини, що
проходить через три точки.
5.1.4 Взаємне розміщення двох площин.
Нехай дві площини 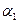 і
і 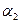 задані загальними рівняннями
задані загальними рівняннями
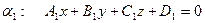

Дві площини паралельні, якщо 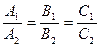
Дві площини перпендикулярні, якщо скалярний добуток їх нормальних векторів 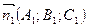 ,
, 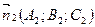 дорівнює нулю:
дорівнює нулю:  .
.
Кут між двома площинами знаходиться як кут між нормальними векторами цих площин 
Відстань від точки  до площини
до площини  обчислюється за формулою
обчислюється за формулою 
5.2 Рівняння прямої у просторі.
5.2.1 Загальне рівняння прямої у просторі можна задати як перетин двох площин

 (1)
(1)
Напрямний вектор прямої, заданої системою (1) обчислюється за формулою

5.2.2 Канонічне рівняння прямої
 Нехай
Нехай  - довільна точка прямої,
- довільна точка прямої,  - напрямний вектор прямої, координати якого обчислюються з системи (1)
- напрямний вектор прямої, координати якого обчислюються з системи (1) 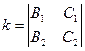


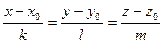 - канонічне рівняння
- канонічне рівняння
5.2.3 Параметричні рівняння прямої


 Þ
Þ 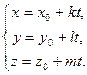 - параметричні рівняння, де
- параметричні рівняння, де  - задана точка, що належить прямій,
- задана точка, що належить прямій,  - напрямний вектор прямої.
- напрямний вектор прямої.
5.2.4 Рівняння прямої, що проходить через дві точки
Якщо пряма проходить через дві точки у просторі  ,
,  , то:
, то:

5.3 Кут між прямою і площиною.
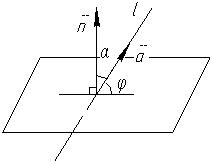 Нехай
Нехай 
 - кут між прямою
- кут між прямою  і площиною
і площиною  ,
, 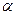 - кут між нормальним вектором
- кут між нормальним вектором  площини
площини  і напрямним вектором
і напрямним вектором  прямої
прямої 
Кут між прямою 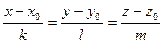 і площиною
і площиною  знаходять за формулою
знаходять за формулою
Умова паралельності прямої 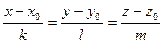 і площини
і площини  :
:

Умова перпендикулярності прямої 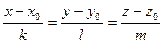 і площини
і площини  :
:
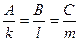
5.4 Окремі випадки завдання площини у просторі
5.4.1 Рівняння площини, яка проходить через задану пряму, перпендикулярно до заданої площини.
Нехай пряма  задана рівнянням
задана рівнянням 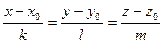 , а площина
, а площина 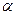 задана рівнянням
задана рівнянням  причому
причому  . Тоді рівняння має вигляд:
. Тоді рівняння має вигляд:

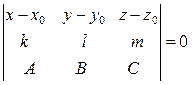
5.4.2 Рівняння площини, яка проходить через дві паралельні прямі.
Дві паралельні прямі  і
і 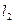 задані відповідно рівняннями
задані відповідно рівняннями


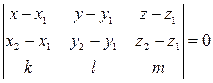 - рівняння шуканої площини.
- рівняння шуканої площини.
5.4.3 Рівняння площини, яка проходить через дві прямі, що перетинаються.
Дві прямі, що перетинаються  і
і 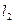 задані відповідно рівняннями
задані відповідно рівняннями
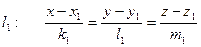

 Тоді:
Тоді:
 - рівняння
- рівняння
шуканої площини.
5.4.4 Рівняння площини, яка проходить через задану пряму і задану точку.
Дана пряма  задана рівнянням
задана рівнянням 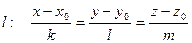 і точка
і точка  (
(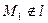 ).
).
Тоді:
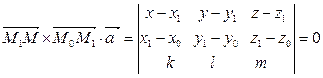 - рівняння шуканої площини.
- рівняння шуканої площини.
Контрольні запитання.
5. Запишіть загальне рівняння площини. Зробіть його досліження.
6. Які умови паралельності та перпендикулярності площин?
7. Запишіть рівняння площини, що проходить через три точки.
8. Запишіть види рівнянь прямої у просторі.
9. Як знайти кут між прямою і площиною?
10. Запишіть рівняння площини, яка проходить через дві паралельні прямі.
11. Запишіть рівняння площини, яка проходить через дві прямі, що перетинаються.
12. Запишіть рівняння площини, яка проходить через задану пряму і задану точку.
Лекція 6. Криві другого порядку. Поверхні другого порядку
План.
1. Вступ.
2. Еліпс (*).
3. Гіпербола (*).
4. Парабола (*).
5. Поверхні другого порядку (*).
Кривою другого порядку називається множина М точок площини, координати яких задовольняють рівняння другого степеня
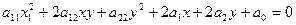 , де
, де  - дійсні числа.
- дійсні числа.
До кривих другого порядку відносяться: коло, еліпс, гіпербола, парабола.
Коло – це геометричне місце точок, кожна з яких рівновіддалена від даної точки, яка називається центром кола.
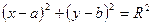 , точка
, точка  - центр кола.
- центр кола.
6.2 Еліпс.
Еліпс – це геометричне місце точок площини, сума відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина стала і дорівнює 2а.

Точка - належить еліпсу,
- належить еліпсу,  і
і 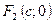 - фокуси,
- фокуси,  і
і  - фокусні радіуси точки М.
- фокусні радіуси точки М.
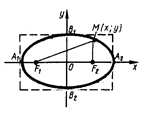
За означенням 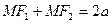

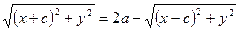
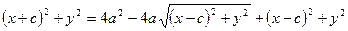
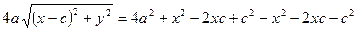
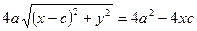
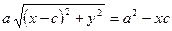


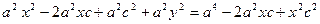



Позначимо 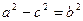 , тоді
, тоді 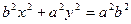 .
.
Поділимо обидві частини цієї рівності на  , тоді
, тоді

 - канонічне рівняння еліпса.
- канонічне рівняння еліпса.
2а – велика вісь, 2в – мала вісь, 2с – фокусна вісь, 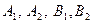 - вершини еліпса
- вершини еліпса
 зв’язок між фокусною відстанню та осями еліпса (
зв’язок між фокусною відстанню та осями еліпса (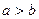 ).
).
Ексцентриситетом еліпса називається відношення фокусної відстані до більшої осі:  . Ексцентриситет вказує на форму еліпса.
. Ексцентриситет вказує на форму еліпса.
Директрисами еліпса називаються прямі, що задаються рівнянням:  .
.
 - рівняння еліпса із зміщеним центром,
- рівняння еліпса із зміщеним центром,  - центр.
- центр.
| 
| |
| Канонічне рівняння | 
| 
|
| Розташування фокусів Координати фокусів Співвідношення між a і b Велика вісь Мала вісь Фокусна відстань Ексцентриситет Співвідношення між a,b,c | F1 ; F2 Î Ox F1(-c;0), F2(c;0) a>b |A1A2|=2a |B1B2|=2b |F1F2|=2c e=c/a a2 - b2 = с2 | F1 ; F2 Î Oy F1(0;c), F2(0;-c) a<b |B1B2|=2b |A1A2|=2a |F1F2|=2c e=c/b b2 - a2 = с2 |
6.3 Гіпербола.
Гіпербола – це геометричне місце точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина стала і дорівнює 2а.

За означенням 
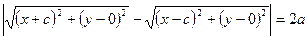
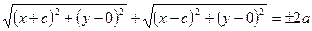

Піднесемо обидві частини рівності до квадрату
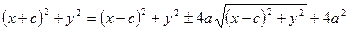

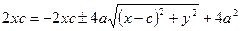

 , піднесемо обидві частини рівності до квадрату
, піднесемо обидві частини рівності до квадрату
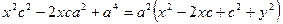

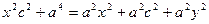
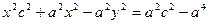

Позначимо  , тоді
, тоді 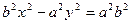 .
.
Поділимо обидві частини цієї рівності на  , тоді
, тоді
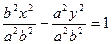
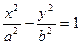 - канонічне рівняння гіперболи.
- канонічне рівняння гіперболи.
2а – дійсна вісь, 2в – уявна вісь, 2с – фокусна вісь, 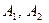 - вершини гіперболи
- вершини гіперболи
 зв’язок між фокусною відстанню та осями гіперболи (
зв’язок між фокусною відстанню та осями гіперболи (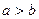 ).
).
Ексцентриситетом гіперболи називається відношення відстані між фокусами до відстані між вершинами: 
Директрисами гіперболи називаються прямі, що задаються рівнянням:
 .
.
Діагоналі прямокутника є асимптотами гіперболи. Асимптоти гіперболи задаються рівняннями: 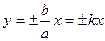
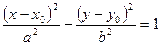 - рівняння гіперболи із зміщеним центром,
- рівняння гіперболи із зміщеним центром,  - центр.
- центр.
Якщо 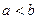 , то
, то 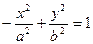
Гіперболи 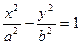 та
та 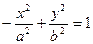 називаються спряженими.
називаються спряженими.

| 
| |
| Канонічне рівняння | 
| 
|
| Розташування фокусів Координати фокусів Дійсна вісь Уявна вісь Фокусна відстань Ексцентриситет Співвідношення між a,b,c | F1 ; F2 Î Ox F1(-c;0), F2(c;0) |A1A2|=2a |B1B2|=2b |F1F2|=2c e=c/a с2 = a2 + b2 | F1 ; F2 Î Oy F1(0;c), F2(0;-c) |B1B2|=2b |A1A2|=2a |F1F2|=2c e=c/b c2 = a2 + b2 |
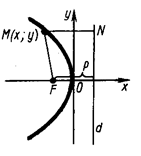
Парабола – це геометричне місце точок площини, рівновіддалених від фіксованої точки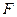 , та фіксованої прямої
, та фіксованої прямої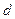 (
(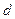 не проходить через
не проходить через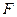 ).
).
Точка 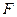 називається фокусом, пряма
називається фокусом, пряма 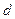 називається директрисою.
називається директрисою.
Розмістимо систему координат так, щоб точка 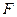 знаходилась на осі Ох, директриса була перпендикулярною до осі Ох, а точка
знаходилась на осі Ох, директриса була перпендикулярною до осі Ох, а точка  ділила відстань між фокусом і директрисою пополам:
ділила відстань між фокусом і директрисою пополам:  .
.
 Позначимо
Позначимо 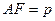 , тоді
, тоді  тому
тому  ,
, 
Директриса задається рівнянням: 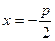
За означенням параболи 


Піднесемо обидві частини рівності до квадрату


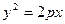 - канонічне рівняння параболи, симетричної відносно осі Ох.
- канонічне рівняння параболи, симетричної відносно осі Ох.
 - канонічне рівняння параболи, вершина якої знаходиться в
- канонічне рівняння параболи, вершина якої знаходиться в
точці 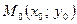

| 
| |
| Канонічне рівняння | 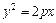
| 
|
| Розташування фокуса | На додатній піввісі Ox | На від’ємній піввісі Ox |
| Координати фокуса | 
| 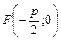
|
| Рівняння директриси | 
| 
|
 |
6.5 Поверхні другого порядку
Пове́рхня — геометричне поняття, при логічному уточненні якого, в різних розділах геометрії йому надається різний зміст.
У елементарній геометрії - це площина, багатогранник, а також деякі «криві поверхні». При цьому кожна поверхня визначається спеціальним способом, без загального означення, найчастіше як множина точок, котрі задовольняють певні умови. Наприклад, сфера — множина точок, котрі знаходяться на однаковій відстані від однієї точки, котру називають центром сфери.
Поняття «поверхні» лише пояснюється, а не визначається. Наприклад, кажуть, що поверхня є границею тіла чи слідом рухомої лінії.
У сучасній геометрії поверхнею називають двовимірну множину, двовимірну підмножину, але інколи навіть так означають довільну множину точок.
Означення Поверхнею другого порядку називається множина точок, прямокутні координати яких задовольняють рівняння виду:
ах2 + by2 + cz2 + dxy + exz + fyz + gx + hy + kz + l = 0,
де принаймні один з коефіцієнтів а, b, c, d, e, f відмінний від нуля. Це рівняння називається загальним рівнянням поверхні другого порядку.
| Еліпсоїд— замкнута центральна поверхня другого порядку. Еліпсоїд має центр симетрії та три осі, які називаються осями еліпсоїда. Точки перетину координатних осей з еліпсоїдом називаються його вершинами. Січення еліпсоїду площинами є еліпсами (зокрема, завжди можна вказати кругові січення еліпсоїду). |
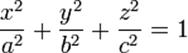
| 
|
| Сфе́ра -замкнута поверхня, геометричне місце точок рівновіддалених від даної точки, що є центром сфери. | 
| 
|
| Еліптичний параболоїд виглядає як овальна чашка й може мати точку максимуму або мінімуму. |
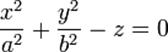 де a, b, с- дійсні півосі
де a, b, с- дійсні півосі
|

|
| Гіперболічний параболоїд (не плутати з гіперболоїдом) — це двічі лінійчаста поверхня, що має вигляд сідла. | 
|

|
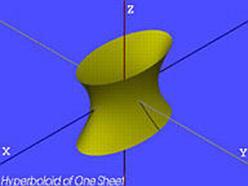
| Гіперболоїд однолистовий | 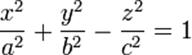 де a і b- дійсні півосі, а c- уявна піввісь;
де a і b- дійсні півосі, а c- уявна піввісь;
| 
|
| Гіпеболоїд дволистовий |
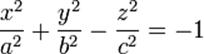 де a і b - уявні півосі, а c- дійсна піввісь. де a і b - уявні півосі, а c- дійсна піввісь.
| 
|
| Конус |

| 
|
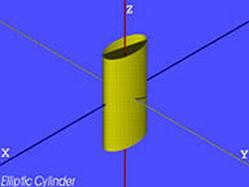
| Еліптичний циліндр |

| 
|
| Гіперболічний циліндр |

| 
|
| Параболічний циліндр |

| 
|
Контрольні запитання  .
.
1. Що називається лінією другого порядку?
2. Що називається колом? Запишіть його рівняння.
3. Що називається еліпсом? Виведіть його рівняння.
4. Що називається ексцентриситетом, директрисами еліпса?
5. Що називається гіперболою? Виведіть її рівняння.
6. Що називається ексцентриситетом, директрисами, асимптотами гіперболи?
7. Що називається параболою? Виведіть її рівняння.
8. Яке рівняння параболи, симетричної відносно осі Ох, Оу?
9. Які поверхні другого порядку можете вказати, які їх рівняння?
Лекція 7. Числові функції та числові послідовності, їх
властивості. Границя функції в точці.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2433; Нарушение авторских прав?; Мы поможем в написании вашей работы!