Приклади обчислення границь

План.

4. Границя функції при умові (*).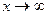

5. Нескінченно малі та нескінченно великі функції (*).

6. Важливі границі (**).

7. Приклади обчислення границь (***).

8.1 Границя функції при умові .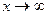

На малюнку показано функцію, для якої виконується умова: якщо значення аргумента необмежено зростають, то значення функції f (x)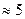. В подальшому той факт, що значення аргумента необмежено зростають будемо записувати тиким чином: x 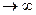. Тоді число 5 будемо називати границею даної функції при умові, що x .

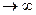Означення. Число А називається границею даної функції при х, що прямує до плюс нескінченності, якщо для любого числа існує таке додатнє число М, що при всіх значеннях аргумента х з області визначення, таких, що x > M, виконується нерівність | f (x) – А| < .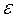

Використовують таку форму запису: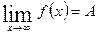

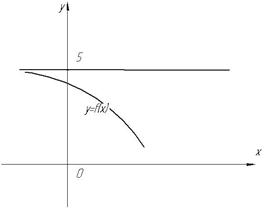На малюнку показано функцію, для якої виконується умова: якщо значення аргумента необмежено ззменьшується, то значення функції f (x)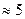. В подальшому той факт, що значення аргумента необмежено зменьшується будемо записувати тиким чином: x 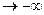. Тоді число 5 будемо називати границею даної функції при умові, що x .

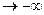Означення. Число А називається границею даної функції при х, що прямує до мінус нескінченності, якщо для любого числа існує таке додатнє число М, що при всіх значеннях аргумента х з області визначення, таких, що x < –M, виконується нерівність | f (x) – А| < .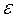

Використовують таку форму запису: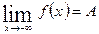

8.2 Нескінченно великі та нескінченно малі функції.

Означення. Функція 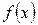називається нескінченно великою величиною при

, якщо .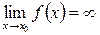

Властивості нескінченно великих функцій.

1. Якщо при функція f(x) має скінченну границю 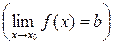, а функція j(x) – нескінченно велика 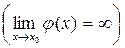, то сума цих функцій – нескінченно велика функція, тобто 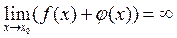; а границя відношення f(x) до j(x) дорівнює нулю:

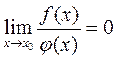
2. Добуток двох нескінченно великих функцій – функція нескінченно велика,

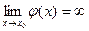тобто, якщо і , то

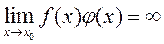
Означення. Функція називається нескінченно малою величиною при 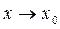, якщо .

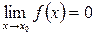Властивості нескінченно малих функцій:

1. Якщо функція f(x) нескінченно мала при , то і функція 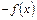також є нескінченно малою при .

2. Якщо функції f(x) і j(x) нескінченно малі при , то їх сума і різниця f(x)+j(x), f(x)-j(x) також є нескінченно малими функціями при .

3. Якщо при функція f(x) нескінченно мала, а функція j(x) – обмежена, то їх добуток f(x)j(x) – нескінченно мала функція.

Зв’язок між нескінченно малими і нескінченно великими функціями.

1. Якщо f(x) при - нескінченно велика функція, то функція - нескінченно мала.

2. Якщо при функція j(x) - нескінченно мала, то функція 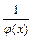- нескінченно велика, при цьому функція j(x) не перетворюється на нуль в околі точки x ₀ .

Правила порівняння нескінченно малих величин.

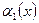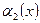Нехай і нескінченно малі величини при , тоді:

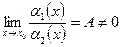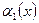1) якщо , то і 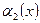називаються нескінченно малими одного порядку;

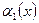2) якщо , то називається нескінченно малою вищого порядку, ніж ;

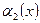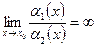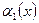3) якщо , то називається нескінченно малою нижчого порядку, ніж ;

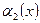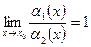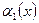4) якщо , то і 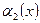називаються еквівалентними нескінченно малими ();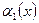

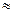
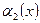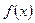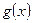Приклад. Довести, що функції і при 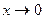є нескінченно малими одного порядку, якщо і .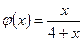

Тоді: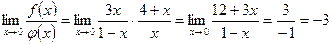

Основні пари еквівалентних нескінченно малих функцій.

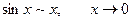
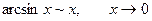
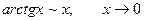
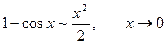
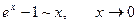
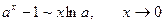
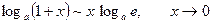
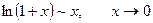
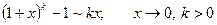
Приклад. Користуючись основними еквівалентностями, обчислити границю.

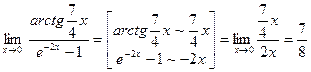
8.3 Важливі границі.

При обчисленні границь часто використовують такі границі:

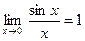- перша важлива границя

Наслідки:

1)

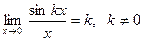
2)

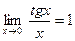
3)

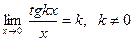
4)

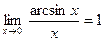
5)

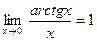
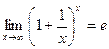- друга важлива границя

Наслідки:

1)

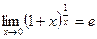
2)

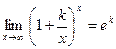
Приклади. Обчислити границі.

1. Границя функції, яка представляє собою многочлен, при 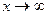є нескінченність.

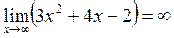
2. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника і знаменника однакові дорівнює відношенню коефіцієнтів при старших членах.

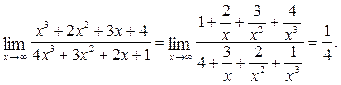
3. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника менша за степінь знаменника, дорівнює нулю.

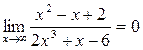
4. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника більша за степінь знаменника, дорівнює нескінченності.

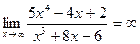
5.

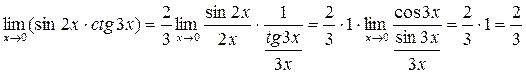
6.

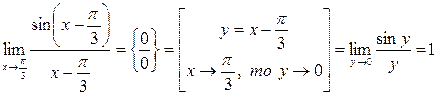
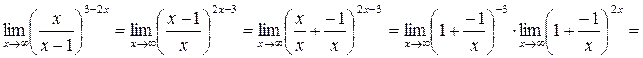
7.

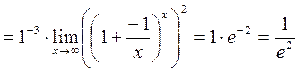
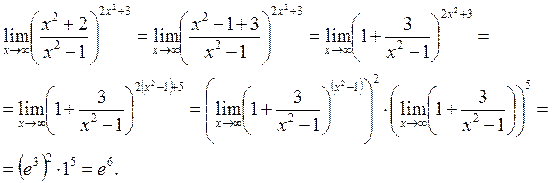
8.

Контрольні запитання.

6. Яка функція називається нескінченно малою, нескінченно великою?

7. Сформулюйте властивості нескінченно малих величин.

8. Сформулюйте правила порівняння нескінченно малих величин.

9. Назвіть основні пари еквівалентних нескінченно малих функцій.

10. Запишіть першу та другу важливі границі.

Лекція 9. Неперервність функції.

Дата добавления: 2014-01-15