
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади обчислення границь
|
|
|
|
План.
1. Поняття числової послідовності та її границі. Число e (*).
2. Функція. Границя функції в точці. Правила обчислення границь (**).
3. Приклади обчислення границь (*).
7.1 Поняття числової послідовності та її границі. Число e.
Означення. Числова функція 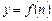 , область визначення якої є множина натурального ряду чисел, називається числовою послідовністю, або просто послідовністю, і позначається
, область визначення якої є множина натурального ряду чисел, називається числовою послідовністю, або просто послідовністю, і позначається  , надалі писатимемо
, надалі писатимемо 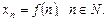
Значення  називаються членами послідовності. Послідовність вважається заданою, якщо задано n -й член послідовності.
називаються членами послідовності. Послідовність вважається заданою, якщо задано n -й член послідовності.
Приклад. Записати три перші члени послідовності 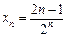 . Маємо
. Маємо 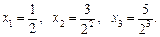
Приклад. За заданими трьома першими членами послідовності  знайти формулу n -го члена.
знайти формулу n -го члена.
Задача розв’язується методом добору з наступною перевіркою  .
.
Означення. Число а називається границею послідовності 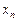 , якщо для будь-якого
, якщо для будь-якого 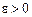 , яке б мале воно не було, існує номер N такий, що для всіх номерів
, яке б мале воно не було, існує номер N такий, що для всіх номерів  виконується нерівність
виконується нерівність  .
.
Позначення 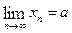 .
.
Для стислого запису означення границі використаємо квантори:
" — для будь-якого, будь-який;
$—існує,знайдеться;
: = дорівнює за означенням, означає.
Тоді означення границі послідовності за допомогою цих символів запишеться так:
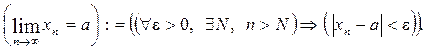
Розглянемо геометричну інтерпретацію границі послідовності. На числовій осі побудуємо e-окіл числа а, тобто інтервал (а – e; а + e), і покажемо, як розміщуватимуться точки, які відповідають членам послідовності  , при
, при 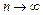 .
.
Таким чином, число а називається границею послідовності xn, якщо для будь-якого e-околу точки а існує номер N такий, що, починаючи з номерів  , усі члени послідовності перебувають в e-околі точки а.
, усі члени послідовності перебувають в e-околі точки а.
Означення. Послідовність називається збіжною, якщо вона має границю (скінченну). Послідовність, яка не має границі, називається розбіжною.
Збіжні послідовності мають властивості:
Теорема 1. (Єдиність границі послідовності). Якщо послідовність має границю, то вона єдина.
Теорема 2. (Необхідна умова збіжності послідовності). Якщо послідовність збіжна, то вона обмежена.
Розглянемо послідовність 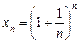 . Можна довести, що ця послідовність монотонно зростає і обмежена
. Можна довести, що ця послідовність монотонно зростає і обмежена  .
.
Існує границя цієї послідовності, яку позначають так: 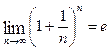 .
.
Зазначимо, що число е = 2,7183... є основою натуральних логарифмів 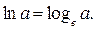 Взагалі, число е, як і число p = 3,14..., широко застосовують при розв’язку різноманітних задач з різних галузей знань.
Взагалі, число е, як і число p = 3,14..., широко застосовують при розв’язку різноманітних задач з різних галузей знань.
7.2 Функція. Границя функції в точці. Правила обчислення границь.
Означення. Функцією y = f (x) називається така відповідність між множинами D i E, за якої кожному значенню змінної х відповідає одне й тільки одне значення змінної у.
При цьому вважають, що:
х — незалежна змінна, або аргумент;
у — залежна змінна, або функція;
f — символ закону відповідності;
Е —область визначення функції;
D — множина значень функції.
Розрізняють три способи завдання функції: аналітичний, графічний і табличний.
Означення. Функція у = F (u), де u = j(x), називається складною (складеною) функцією, або суперпозицією функцій F (u) та j(х), і позначається y = F (j (x)).
Нехай функція 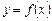 визначена у деякому околі точки х = x0 за винятком, хіба що, самої точки х = x0.
визначена у деякому околі точки х = x0 за винятком, хіба що, самої точки х = x0.
Означення. Число А називається границею функції 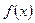 при
при  , якщо для довільного
, якщо для довільного  існує число
існує число 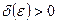 таке, що для всіх
таке, що для всіх , які задовольняють нерівність:
, які задовольняють нерівність: 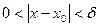 , виконується нерівність
, виконується нерівність 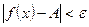 .
.
 Пишуть:
Пишуть: 
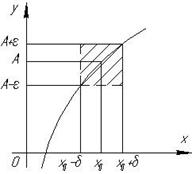
На малюнку показано:
 -
- 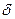 - окіл точки
- окіл точки 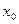
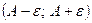 -
- 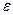 - окіл точки А
- окіл точки А
Тоді геометрично це означає: що будь – якій точці з
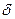 - околу відповідає деяка точка з
- околу відповідає деяка точка з 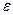 - околу.
- околу.
Функція f(x) не може мати двох різних границь в одній точці.
Розглянемо основні властивості границь при умові, що кожна з функцій 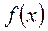 і
і 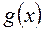 має скінченну границю при
має скінченну границю при 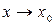 :
:
1) 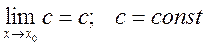
2) 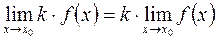
3) 
4) 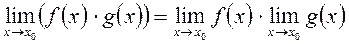
5) 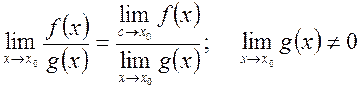
Наслідки:
1. Постійний множник можна виносити за знак границі 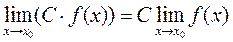 для будь-якого постійного числа С.
для будь-якого постійного числа С.
2. Якщо 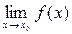 існує, то для довільного натурального m має місце формула:
існує, то для довільного натурального m має місце формула:

Приклад 1: Знайти 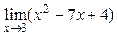 .
.
Розв’язок.
Функція 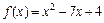 - ціла раціональна. Замінимо в аналітичному виразі функцію x його граничним значення і отримаємо
- ціла раціональна. Замінимо в аналітичному виразі функцію x його граничним значення і отримаємо
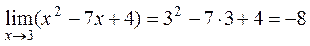 .
.
Приклад 2: Знайти 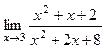 .
.
Розв’язок.
Будемо шукати границю дробово-раціональної функції. Перш ніж підставляти граничне значення x, перевіримо, чи не обертається в нуль знаменник дробу при x = 3.
Перевіряємо: 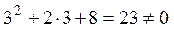
Тоді:
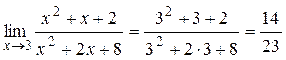 .
.
Приклад 3: Якщо чисельник функції – стала величина, а границя знаменника дорівнює нулю, то границя такої функції є нескінченність.
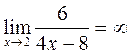
Приклад 4: Якщо функція дробово – раціональна, то для знаходження границі чисельник і знаменник розкладають на множники, які потім скорочують, причому скоротитись повинен той множник, який обертається в нуль
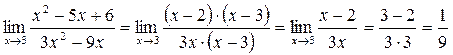
Приклад 5: Якщо функція містить знаки радикалів, то чисельник і знаменник помножають на вираз, спряжений до чисельника (знаменника), а потім застосовують формулу різниці квадратів. Вирази 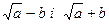 та
та 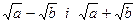 називаються спряженими.
називаються спряженими.
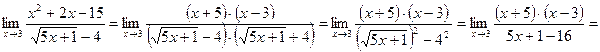
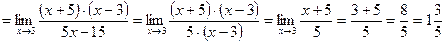
Приклад 5: Якщо функція містить корінь третього степеня, то чисельник і знаменник помножають на неповний квадрат суми або різниці, а потім застосовують формулу суми або різниці кубів.
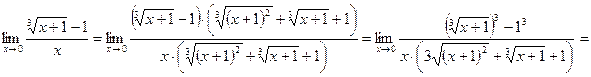
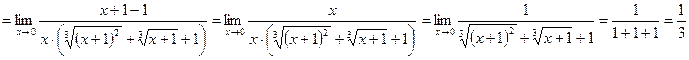
Контрольні запитання.
1. Що називається послідовністю?
2. Що називається границею числової послідовності?
3. Що називається границею функції?
4. Сформулюйте властивості границь.
5. Сформулюйте та покажіть на прикладах правила обчислення границь.
Лекція 8. Нескінченно малі та нескінченно великі функції.
Важливі границі.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 6675; Нарушение авторских прав?; Мы поможем в написании вашей работы!