Приклад. 36. Інтегрування виразів, що містять квадратний тричлен (**)

План.

36. Інтегрування виразів, що містять квадратний тричлен (**).

37. Інтегрування раціональних функцій (**).

15.1. Інтегрування виразів, що містять квадратний тричлен.

1. Розглянемо інтегрування інтеграла вигляду: .

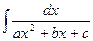Даний інтеграл шляхом виділення повного квадрата у знаменнику можна звести до знаходження інтегралів більш простого виду:

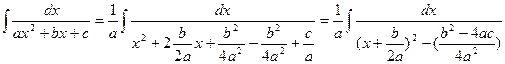
Позначимо: і .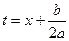

Тоді інтеграл набирає вигляду:

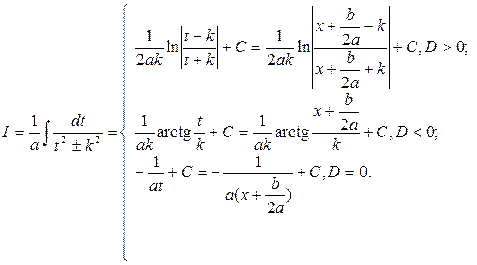
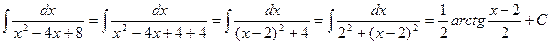
2. Розглянемо інтегрування інтеграла

.

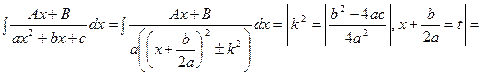
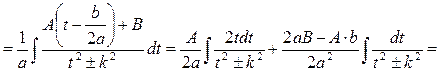
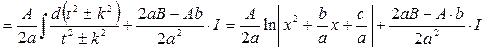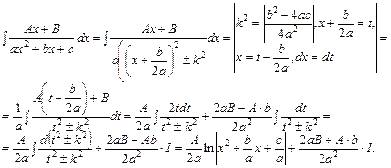
Інтеграл І залежно від знака дискримінанта 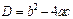буде таким:

Приклад.

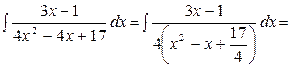
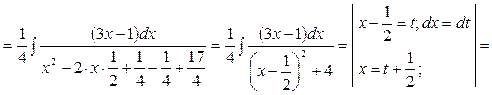
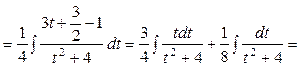
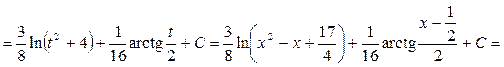
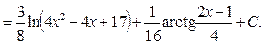
3. 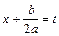Інтеграли виду 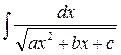можна за допомогою підстановки 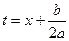привести до інтегралу вигляду .

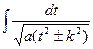При цьому для a>0 маємо:

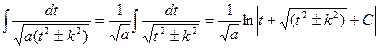
Якщо a<0:

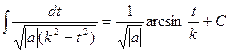
Приклад:

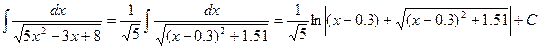
4. Розглянемо . Аналогічно попередньому можна показати:

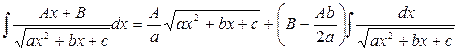
Приклад:

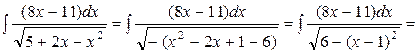
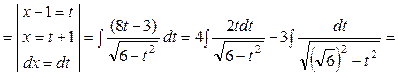
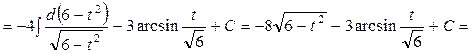
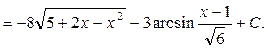
5. Розглянемо 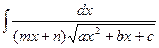. За допомогою підстановки

та 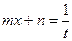можна отримати 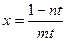; ; 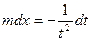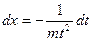, що дасть змогу звести інтеграл до раніше розглянутих.

6. Розглянемо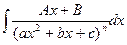

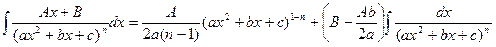
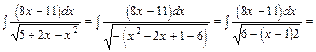
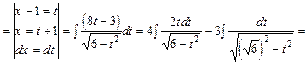
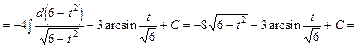
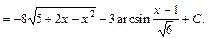
15.2 Інтегрування раціональних функцій

Означення. Відношення двох многочленів 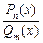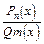називаєть­ся раціональним дробом.

Означення. Раціональний дріб 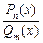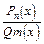називається правильним, якщо степінь многочлена в чисельнику менший від степеня многочлена в знаменнику, тобто n < m; якщо n ³ m, то дріб називається неправильним.

Теорема. Будь-який неправильний раціональний дріб можна подати у вигляді суми многочлена (цілої частини) та правильного раціонального дробу.

Означення. За домовленістю найпростішими раціональними дробами називаються такі дроби чотирьох типів:

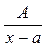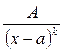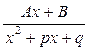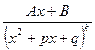І.; ІІ. ; ІІІ. ; IV. , де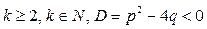

Інтеграли від вказаних дробів мають вигляд:

І. ;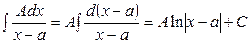

ІІ. ;

ІІІ. 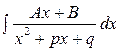— розглянуто в попередньому пункті;

IV. — інтегрується за допомогою рекурентних формул.

Теорема 6. Будь-який правильний раціональний нескоротний дріб 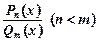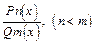можна подати у вигляді скінченної кількості найпростіших дробів, використовуючи такі правила:

1). Якщ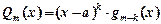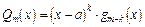о , , то:

;

2). Якщ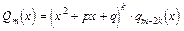о , то:

,

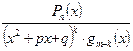
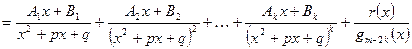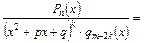
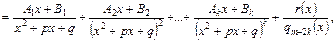
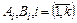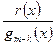
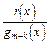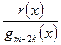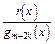де А_і, В_і, і = — деякі коефіцієнти, та — правильні раціональні дроби.

Методика інтегрування раціональних функцій:

- якщо підінтегральна функція — неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена та правильного раціонального дробу;

- знаменник правильного раціонального дробу розкладають на множники. За виглядом знаменника правильний раціональний дріб подають у вигляді суми найпростіших дробів, використовуючи метод невизначених коефіцієнтів;

- інтегрують цілу частину та найпростіші дроби.

Приклад. Знайти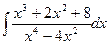

Степінь чисельника меньше ніж степінь знаменника, тому підінтегральна функція є правильним раціональним дробом.

Тоді:

Зводимо до спільного знаменника праву частину і знаменники не розглядаємо.

.

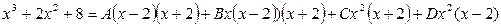У правій частині розкриємо дужки та згрупуємо за степенями х.

Прирівнюючи коефіцієнти при однакових степенях х, отримаємо систему:

; ; ; .

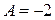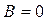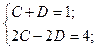
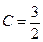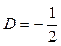Отже, .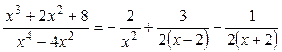

Тоді:

Приклад Знайти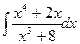

Степінь чисельника більше ніж степінь знаменника, тому підінтегральна функція є неправильним раціональним дробом.

Тоді поділемо чисельник на знаменник:

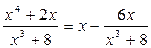
Далі:

;

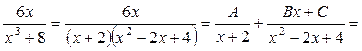
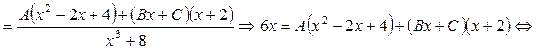
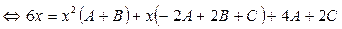Маємо систему рівнянь:

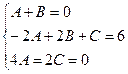звідки А=-1, В=1, С=2

Тоді:

.

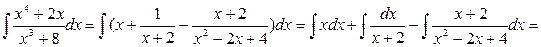
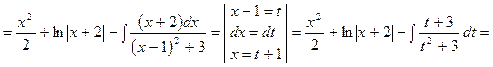
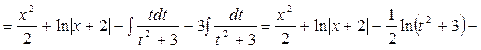
Контрольні запитання.

29. Які випадки інтегрування функцій, що містять квадритний тричлен можна вказати? Наведіть приклади знаходження інтегралів

30. Які раціональні дроби відносяться до правильних і неправильних? Наведіть приклади.

31. В чому сутність методу невизначених коефіцієнтів? Наведіть приклади.

Лекція 16. Інтегрування різних функцій.

Дата добавления: 2014-01-15