
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Ейлера
|
|
|
|
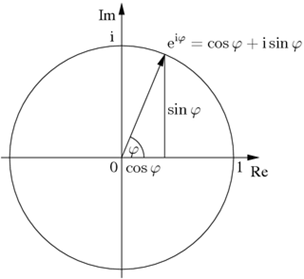
Формула Ейлера:
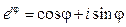 ,
,  ,
,
 ,
, 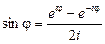 .
.
В загальному випадку:

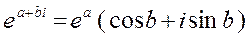
За допомогою формули Ейлера можна дістати показникову форму комплексного числа: 
Контрольні запитання.
1. Які числові множини можна вказати?
2. Які існують форми запису комплексних чисел? Наведіть приклади.
3. Які дії над комплексними числами можна виконувати? Наведіть приклади.
4. Як здійснити перехід від алгебраічної до тригонометричної форми комплексного числа? Наведіть приклади.
5. Як виконати дії над комплексними числами в тригонометричній формі? Наведіть приклади.
6. Запишіть формулу Ейлера для комплексного числа. Поясніть її елементи.
Лекція 23. Основні поняття теорії диференціальних рівнянь.
Диференціальні рівняння першого порядку.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 696; Нарушение авторских прав?; Мы поможем в написании вашей работы!