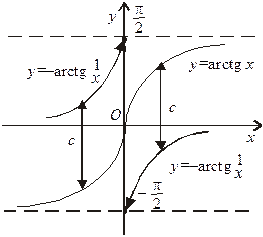Адаптивные рулевые

Типовые аналоговые авторулевые.

План.

64. Основні поняття.

65. Диференціальне рівняння першого порядку (*).

66. Диференціальне рівняння з відокремленими та відокремлюваними змінними (**).

67. Однорідне диференціальне рівняння (**).

68. Лінійні диференціальні рівняння (**).

69. Рівняння Бернуллі (**).

23.1 Основні поняття.

Означення. Звичайним диференціальним рівнянням називається рівняння, яке зв’язує незалежну змінну, функцію та її похідні.

Порядок диференціального рівняння визначає найвища похідна, яка входить у рівняння.

У загальному випадку диференціальне рівняння n -го порядку має вигляд:

Далі замість слів «диференціальні рівняння» будемо використовувати скорочення ДР.

При вивченні ДР будемо розглядати лише диференціальні рівняння, в яких шукана функція залежить лише від одного аргументу. Такі рівняння називаються звичайними.

Загальним розв’язком диференціального рівняння є всяка функція, яка при підстановці її у рівняння перетворює його у тотожність. Якщо сталі, що входять до загального розв’язку, можна знайти виходячи з певних початкових умов, то буде знайдено частинний розв’язок ДР.

23.2 Диференціальне рівняння першого порядку.

Диференціальне рівняння першого порядку має вид 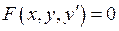або .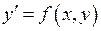

Загальним розв’язком цього рівняння є функція виду y = f (x,C), яка при довільних значеннях сталої величини 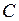є розв’язком цього рівняння. Для знаходження частинного (єдиного) розв’язку необхідно знати початкові умови, які для рівняння першого порядку записують у вигляді або .

Тоді задача пошуку розв’язку y = f (x,C), що задовольняє умови y = y₀ при x = x₀ називається задачею Коші. Геометрично функція y = f (x,C) описує множину інтегральних кривих на числовій площині.

Означення. Множина кривих, залежних від параметра, називається сім’єю кривих.

Таким чином, задачу інтегрування ДР пер­шого порядку можна розглядати як задачу пошуку рівняння сім’ї кривих y = f (x,C) за ДР, яке описує цю сім’ю.

Для наближеного знаходження сім’ї інтегральних кривих використовується графічний метод. ДР першого порядку задає кутовий коефіцієнт дотичної до інтегральної кривої в кожній точці (х, у).

Якщо в кожній точці (х, у) визначений напрям деякого век­тора, то кажуть, що задано поле напрямів. ДР задає поле напрямів дотичних. Ці лінії, на яких дотичні мають однаковий нахил, називаються ізоклінами. Рівняння ізоклін Побудував­ши графіки ізоклін, можна наближено провести інтегральні криві.

Не існує єдиного універсального методу, за допомогою якого можна розв’язати диференціальні рівняння першого порядку. Існує певний клас рівнянь, які можна розв’язати (проінтегрувати). Розглянемо такі рівняння.

23.3 Диференціальне рівняння з відокремленими та відокремлюваними змінними.

Означення. ДР виду M(x)dx + N(y)dy = 0 називається ДР з відокремленими змінними.

Загальний розв’язок ДР подається так:

а розв’язок задачі Коші з початковими умовами має вигляд

ДР з відокремленими змінними зводиться до до знаходження інтегралів.

Приклад. Знайдемо загальний розв’язок ДР

Інтегруючи, дістаємо інтеграл ДР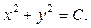

Інтегральними кривими є концентричні кола з центром у почат­ку координат.

Означення. Диференціальне рівняння виду

називається ДР з відокремлюваними змінними, тобто рівнянням, що зводяться до ДР з відокремленими змінними.

Поділивши вказане рівняння на 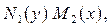дістанемо ДР з відокремленими змінними:

Рівняння має розв’язок 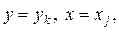де 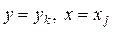є розв’язками рівнянь

Аналогічно ДР виду є ДР з відокремлюваними змінними. Його можна записати у вигляді:

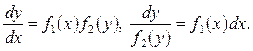
Рівняння має розв’язок виду де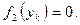

Приклад. Знайдемо загальний розв’язок ДР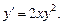

Запишемо рівняння у вигляді

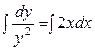
або

23.4 Однорідне диференціальне рівняння.

Означення. Диференціальне рівняння називається однорідним, якщо його можна подати у вигляді

Воно за допомогою заміни змінної зводиться до ДР з відокремлюваними змінними 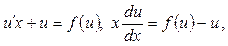а знаходження розв’язку зводиться до інтегрування:

Приклад. Знайдемо загальний розв’язок ДР .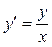

Узявши 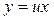, дістанемо ДР і його загальний розв’язок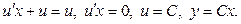

Приклад. Знайдемо загальний розв’язок ДР .

Візьмемо 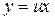і одержимо ДР для змінної

.

Інтегруючи ДР з відокремленими змінними, знаходимо загальний розв’язок: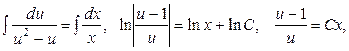

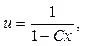
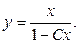
23.5 Лінійні диференціальні рівняння.

Означення. Диференціальні рівняння виду називається лінійним ДР.

Якщо Q (x) = 0, то ДР є однорідним. Якщо Q (x) 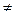0, то ДР називається неоднорідним.

Лагранж запропонував загальний метод розв’язування неоднорідних лінійних ДР. Спочатку розв’язується однорідне ДР. У загальний розв’язок входять довільні сталі. Потім шукається загальний розв’язок неоднорідного ДР і при цьому довільні сталі стають новими шуканими функціями.

Шукатимемо розв’язок неоднорідного ДР у два етапи. Спочатку розв’яжемо однорідне ДР .

,

.

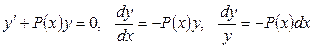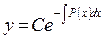Таким чином, загальний розв’язок має вигляд .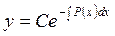

Далі шукаємо розв’язок неоднорід­ного ДР у вигляді 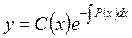, вважаючи С функцією від х. Підставляючи в початкове ДР, дістаємо рівняння:

.

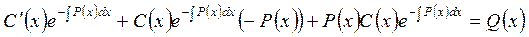Приходимо до простого ДР

Загальний розв’язок неоднорідного ДР запишемо у вигляді:

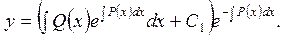
Метод Лагранжа часто називають методом варіації довільної сталої.

23.6 Рівняння Бернуллі.

Означення. Рівняння виду

,

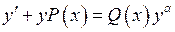де 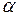– довільне число і яке називають рівнянням Бернуллі.

Рівняння такого типу також можна розв’язати методом варіації довільної сталої.

Контрольні запитання.

47. Що називається диференціальним рівнянням?

48. Що називається рішенням диференціального рівняння?

49. Що називається порядком диференціального рівняння?

50. Які типи диференціальних рівняннь І порядку можете назвати? Покажіть на прикладах.

51. Поясніть методи розв’язування різних типів диференціальних рівняннь І порядку.

Дата добавления: 2014-01-15