События. Алгебра событий

Тема 1. Случайные события

Одним из наиболее важных понятий в теории вероятностей является понятие эксперимента.

Эксперимент состоит в том, что производится испытание при выполнении некоторого ком­плекса условий, которые либо создаются искусственно, либо осуще­ствляются независимо от воли экспериментатора.

Эксперимент задан, если определены его условия и указаны события, наступление или не наступление которых следует наблюдать.

Эксперименты можно разделить на два класса: детерми­нированные и случайные.

В детерми­нированных экспериментах результаты экспериментов заранее предсказуемы на основании есте­ственнонаучных законов.

В случайных (стохастиче­ских) или вероятностных экспериментах при одних и тех же условиях возможно наступление исключающих друг друга событий. Теоретическое изучение таких экспериментов и составляет предмет теории вероятностей.

Примеры случайных экспериментов.

1. Изделия выпускаются партиями по n штук. Проверка качества изделий приводит к их разрушению. Поэтому для проверки партии на качество отбирают m изделий (m < n). Эксперимент заключается в выборе m изделий из партии и их проверке. Результат экспери­мента — число обнаруженных дефектных изделий.

2. Розыгрыш лотереи можно рассматривать как случайный экс­перимент, результатом которого является выпадение выигрышей на определенные лотерейные билеты.

3. В биологическом опыте самоопыления растение, полученное перекрестным опылением двух сортов, наследует по каждому при­знаку гены обоих родителей. Нельзя сказать заранее, как эти гены скомбинированы в том или ином семени, полученном в результате самоопыления: по каждому гену (если он различен в материнском и отцовском сорте) возможны три комбинации: доминантный — до­минантный, доминантный — рецессивный, рецессивный — рецессивный. Следовательно, такой опыт можно рассматривать как случайный эксперимент.

4. Взвешенная в жидкости частица движется в результате столкновений с молекулами жидкости, находящимися в хаотическом тепловом движении. Опыт, в котором наблюдается движение такой частицы, можно рассматривать как случайный эксперимент, резуль­татом которого является траектория движения броуновской частицы.

Рассмотрим множество W событий, кото­рые можно наблюдать в некотором стохастическом эксперименте. События обозначаются буквами A,B,C ….

Выделим два специальных события:

достоверное со­бытие U, 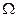, которое обязательно происходит в эксперименте,

невозможное событие V, 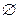, которое не может произойти в эксперименте.

Элементарным событием 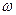называется каждый неразложимый исход опыта.

Множество всех элементарных событий обозначим .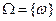

Пример. При бросании монеты

При бросании игральной кости

Событием A назовем любое подмножество 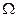: A 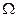(рис.1, а).

Пример. Выпадение нечетного числа при бросании игральной кости -

Суммой (или объединением) A + В (A U В) событий А и В называется событие, состоящее из тех элементарных событий, которые входят в событие А или в событие В или в то и другое (рис.1,б).

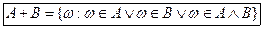
Произведением (или пересечением) АB (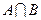) событий A и B называется событие, состоящее из элементарных событий, входящих в событие A и B (рис. 1, в).

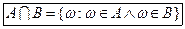
Разностью AB событий A и B называется событие,

состоящее из элементарных событий, входящих в событие

Рис.1 A и не входящих в В (рис. 1,г) AВ = .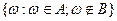

Симметричной разностью называется событие, состоящее из элементарных событий, входящих в событие A и не входящих в В или входящих в событие В и не входящих в А

.

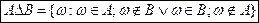Пример. Пусть 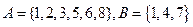. Тогда

Два события A и B несовместимы, если 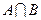, (рис. 1,д).

Для каждого события A 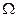введем противоположное собы­тие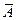(дополнение), которое состоит в том, что событие A не произошло (рис.1,е).

События 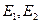, …, 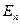образуют полную группу событий, если они попарно несовместимы 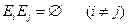и их сумма есть достоверное событие 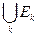= 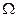, то есть из этих событий происходит одно и только одно (рис. 1, ж).

События A и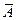образуют полную группу событий

A +=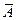

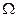
Событие A влечет событие B (A В), если событие B наступает всегда, когда насту­пает A (рис. 1,з).

Случайный эксперимент называется конечным, если имеется полная группа элементарных событий. В теории вероятностей рассматри­ваются лишь такие случайные эксперименты, в которых каждое со­бытие является суммой всех элементарных событий, влекущих это событие. Такой случайный эксперимент описывается множеством элементарных событий 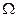(его элементы обозначают буквой 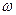с раз­личными индексами, например ) и некоторым классом его подмножеств 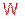, называемых случайными событиями или просто событиями. Этот класс подмножеств должен удовлетворять следующим условиям:

A1. ;

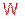A2. ;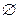

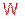A3. A , ;

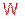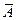
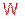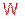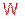A4 A, В , А + В 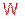, А В , А В .

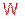Класс подмножеств 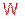, удовлетворяющий условиям 1)—4), называется алгеброй множеств или алгеброй событий.

В том случае, когда 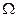конечно, 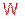совпадает с классом всех подмножеств 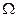. Если 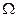содержит n элементов, то количество всех подмножеств 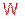равна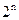

Пример. Пусть , тогда

Если алгебра событий такова, что с бесконечной последовательностью событий 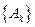она содержит и события 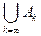и 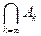, то такая алгебра называется 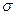- алгеброй (сигма- алгеброй). Событие 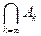обозначает, что все события 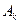происходят одновременно, а событие 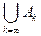состоит в том, что происходит, по крайней мере, одно событие.

Важным примером случайного эксперимента является эксперимент, в котором измеряется некоторая величина 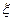. В качестве эле­ментарных событий здесь можно взять события вида (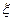= x), где x — некоторое фиксированное значение. Поэтому множество элемен­тарных событий естественно отождествить с множеством точек на прямой. Если априори известно, что 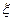может принимать лишь зна­чения из некоторого множества М, то это множество и следует рас­сматривать как множество элементарных событий.

В процессе изме­рения естественно предполагать возможность наблюдения события { а 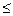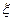< b, а < b }, где a, b — произвольные числа. Всевозможные ко­нечные суммы таких полуинтервалов (а и b могут принимать и бес­конечные значения) можно рассматривать как алгебру событий, связанных с экспериментом.

Таким образом, множество элементарных событий может быть дискретным или непрерывным.

Дата добавления: 2014-01-15