Анализ уравнения движения

Преобразуем уравнение движения (7.15). Приведенный момент в правой части обычно для удобства представляют в виде двух слагаемых: M_Д^ПР – приведенный момент сил движущих, M_С^ПР – приведенный момент сил сопротивления.

(7.16)

Такое разделение вызвано тем, что эти моменты обычно зависят от разных параметров. Например, для машин, приводящихся в движение асинхронными электродвигателями, движущий момент M_Д ими развиваемый, а следовательно и M_Д^ПР является функцией угловой скорости: M_Д = f(w_Д), M_Д^ПР = f(w₁). Силы сопротивления, например, у технологических машин обычно зависят от положения, т.е. M_C^ПР = f(j₁). Возможны и другие случаи.

Рассмотрим физический смысл слагаемых в левой части уравнения (7.16). Первое слагаемое представляет собой инерционный момент, действующий на тело, имеющее угловое ускорение:

Второе слагаемое – это момент, возникающий в том случае, если приведенный момент инерции J^ПР

переменен[1]:

(7.17)

Уравнение (7.16) является обыкновенным в общем случае нелинейным дифференциальным уравнением второго порядка с произвольной правой частью. В общем случае такое уравнение аналитического решения не имеет и, тогда, решается численно, например, одним из методов Рунге-Кутта.

Решением уравнения (7.16) являются функции: w₁(t) и j₁(t). Исключая t как параметр, можно получить функцию w₁(j₁) за цикл движения, например, за один оборот главного вала.

Однако выше была сформулирована задача не только моделирования движения, но и обеспечения требуемой плавности хода. Самый простой способ уменьшить коэффициент неравномерности хода – это установка маховика, который при разгоне машины аккумулирует кинетическую энергию, а при торможении отдает ее. Момент инерции маховика входит составной частью в J^ПР. Например, для машины рассмотренной в подразделе 7.1 общий приведенный момент инерции машины состоит из четырех частей:

J^ПР = J_ГМ^ПР(j₁) + J_ЗМ^ПР + J_РД^ПР + J_М^ПР (7.18)

где J_ГМ^ПР(j₁) – приведенный момент инерции главного механизма,

J_ЗМ^ПР – приведенный момент инерции зубчатого механизма,

J_РД^ПР – приведенный момент инерции ротора двигателя,

J_М^ПР – приведенный момент инерции маховика.

В выражении (7.18) все слагаемые могут быть определены так, как это описано в подразделе 7.4, кроме J_М^ПР. Его значение надо подобрать в процессе решения уравнения движения так, чтобы выполнилось условие (7.3).

При моделировании установившегося режима работы возникает еще одна проблема – определение начальных условий.

Обе этих задачи решаются с помощью алгоритма, представленного на рис. 7.3.

Для обеспечения требуемой плавности хода уравнение (7.16) решается многократно. При этом варьируется значение момента инерции маховика J_М^ПР и контролируется стационарность режима работы. Процесс идет до тех пор, пока не будет найден вариант, удовлетворяющий заданному коэффициенту неравномерности хода.

В блок-схеме приняты обозначения: w₀, w_n – это значения w₁ в начале и конце цикла.

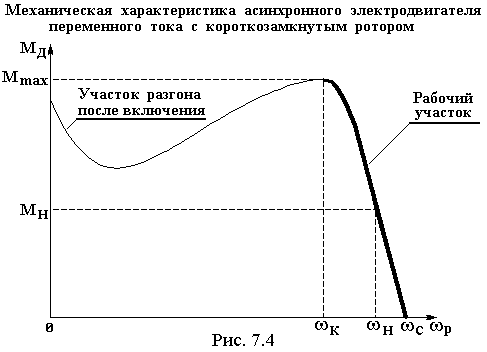
В качестве примера рассмотрим механический пресс, рассмотренный в подразделе 7.1 (см. рис. 7.1). Такие машины чаще всего имеют привод от асинхронного электродвигателя переменного тока. Момент, развиваемый такими двигателями, зависит от многих факторов, но в первом приближении его можно считать зависящим только от угловой скорости ротора. Вид статической механической характеристики асинхронного электродвигателя переменного тока представлен на рис. 7.4.

Характеристика состоит из двух участков. Тонкой линией показан характер изменения момента, развиваемого двигателем в процессе разгона сразу после включения. Рабочая часть характеристики расположена между значениями скорости ротора: w_К – критическая скорость, w_С – синхронная скорость. В этом промежутке находится w_Н – номинальная угловая скорость. В пределах рабочего участка асинхронные двигатели до некоторой степени обладают свойством саморегулирования, т.к. при разгоне ротора момент, развиваемый двигателем уменьшается, а при торможении – увеличивается. Но пределы этого довольно узки.

Характер изменения технологической силы F_T, действующей на пуансон пресса, может быть различен. На рис. 7.5 показан один из возможных вариантов, где s – ход пуансона, s_П – величина его полного хода, s_Р – величина рабочего хода.

На рис. 7.6 представлены решения дифференциального уравнения движения с подбором момента инерции маховика, т.е. результаты работы алгоритма показанного на рис. 7.3.

На рис. 7.6а – графики приведенных моментов, методика вычисления которых рассмотрена выше, где j_Н, j_К – углы поворота кривошипа, соответствующие началу и концу технологической операции. На рис. 7.6б – результаты моделирования движения главного вала. На этой зависимости можно выделить шесть участков. Рассмотрим каждый из них.

Участок 1. Главный вал тормозится т.к. M_Д^ПР < M_С^ПР + M_J^ПР. M_J^ПР на этом участке является моментом сопротивления.

Участок 2. Главный вал разгоняется т.к. M_Д^ПР + M_J^ПР > M_С^ПР. M_J^ПР на этом участке является моментом движущим.

Участок 3. Главный вал резко тормозится т.к. началась технологическая операция и M_С^ПР существенно больше всех остальных моментов.

Участок 4. Главный вал разгоняется т.к. из-за торможения в соответствии с механической характеристикой (см. рис. 7.4) возрос M_Д^ПР и стал больше чем M_С^ПР. M_J^ПР на этом участке существенного влияния на движение не оказывает.

Участок 5. Главный вал тормозится т.к. возрос M_J^ПР, который на этом участке является моментом сопротивления.

Участок 6. Главный вал разгоняется т.к. во-первых M_Д^ПР > M_С^ПР, а кроме того M_J^ПР изменил знак и стал движущим.

Таким образом, колебания угловой скорости главного вала машины в данном случае вызываются двумя причинами:

1. В каждый данный момент времени, приведенный к главному валу момент сил движущих не равен приведенному моменту сил сопротивления.

2. Возникновением дополнительного динамического момента M_J^ПР, вызванного переменностью приведенного момента инерции.

В заключение отметим, что маховик часто не только играет роль выравнивателя скорости. Часто он позволяет уменьшить требуемую мощность двигателя, а, следовательно, и удешевить машину.

В рассмотренном только что примере механический пресс работает в циклическом режиме. Двигатель на каждом обороте главного вала должен восполнить энергию, затраченную на проведение технологической операции. Если бы не было маховика, то двигатель должен был бы восполнить энергию за время технологической операции, которая и производилась бы непосредственно моментом двигателя. При наличии маховика технологическая операция производится в большей степени за счет инерции маховика, а не только моментом двигателя. Двигатель же восполняет потерю энергии в течение всего оборота главного вала. Поэтому и требуется двигатель меньшей мощности. Более того, реальные прессы часто имеют циклом работы не один, несколько оборотов. На первом обороте цикла производится технологическая операция, а потом несколько оборотов идет восстановление скорости.

[1] Действие этого момента можно наблюдать при выполнении фигуристками упражнения “волчок”. Фигуристка начинает вращение с раскинутыми руками, а потом их сводит и при этом резко увеличивается ее скорость вращения. Когда фигуристка сводит руки – уменьшается момент инерции ее тела. Уравнение (7.16) и показывает, что при уменьшении момента инерции возникающий при этом момент M_j^ПР является движущим, а при увеличении – тормозящим.

Дата добавления: 2014-01-15