Параметрический корреляционный анализ

Лабораторная работа №10. Технологии статистических расчетов в MS EXCEL.

Цель: научиться использовать возможности MS Excel для проведения статистических расчетов.

Задачи:

1. Расчет коэффициента корреляции Пирсона и t-статистики Стьюдента.

2. Построение модели регрессии различными способами.

3. Выбор наиболее точной модели связи между двумя величинами.

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятност­ный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей разли­чают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя слу­чайными величинами X и Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин X и Y.

Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффи­циент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.

1. Линейный коэффициент корреляции — параметр, который характеризует степень линей­ной взаимосвязи между двумя выборками, рассчитывается по формуле:

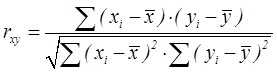
где х_i — значения, принимаемые в выборке X,

y_i — значения, принимаемые в выборке Y;

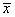— средняя по X, 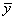— средняя по Y.

Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя вы­борками нет.

Знак коэффициента корреляции очень важен для интерпре­тации полученной связи. Если знак ко­эффициента линейной корреляции — плюс, то связь между кор­релирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина дру­гого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно уве­личивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.

Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе гово­ря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой пере­менной. Такая зависимость носит название обратно пропорцио­нальной зависимости.

Дата добавления: 2014-01-15