Проблема обеспечения точности и достоверности результатов

Проблема обеспечения точности и достоверности результатов можно решить следующим образом. Обозначают точность оценки величиной Е. Из-за наличия стохастичности ограниченности числа опытов N получают оценку 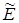. Задаются неравенством

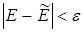(4.72)

и вероятностью P, что неравенство (4.72) выполняется

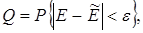(4.73)

где Q – называют достоверностью оценки. Вводят относительную точность оценки

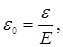(4.74)

с учетом которой достоверная оценка будет равна

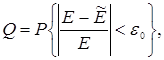(4.75)

Если известен закон распределения 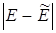, то с помощью анализа формулы (4.73) или (4.75) можно определить количество реализаций N.

В тех случаях, когда закон распределения 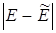найти не удается, то выдвигают предположение о характере закона распределения случайной величины Е.

Рассмотрим взаимосвязь точности и достоверности, когда в качестве показателей эффективности Е, выступают вероятность Р, математическое ожидание а и дисперсия s².

Пусть вероятность появления некоторого события А, которое определяется состояниями процесса функционирования исследуемой системы, равна

Р=Р(А)

В качестве оценки вероятности Р в данном случае выступает

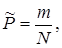
где m - число положительных исходов. Тогда соотношение (4.73), связывающее точность и достоверность оценок с количеством реализаций, будет иметь вид

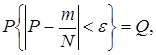
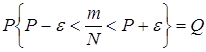(4.76)

Для ответа на вопрос о законе распределения величины представим эту частность в виде

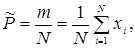
так как количество наступлений события А в данной реализации из N реализаций является случайной величиной x, принимающей значения х₁=1 с вероятностью Р и х₂=0 с вероятностью (1-P).

Математическое ожидание и дисперсия случайной величины x будут равны

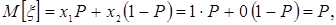
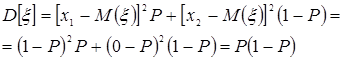
Тогда

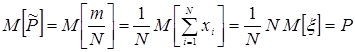
Это соотношение говорит о несмещенности оценки 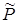для вероятности Р.

С учетом независимости значений величины 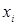получаем

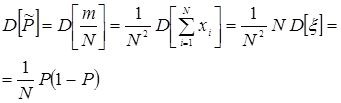
В силу центральной предельной теоремы теории вероятностей при достаточно больших N можно рассматривать частность 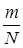как случайную величину, с нормальным законом распределения вероятностей с математическим ожиданием Р и дисперсией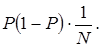

С учетом квантиля нормального распределения вероятностей 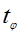точность оценки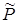

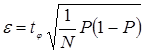(4.77)

Количество реализаций для получения оценки 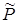с точностью e и достоверностью 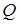будет равно

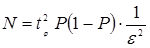(4.78)

Квантиль 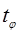порядка 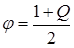находится из специальных таблиц.

Пример. Необходимо рассчитать количество реализаций N при статистическом моделировании системы S, когда в качестве показателя эффективности используется вероятность P при достоверности 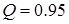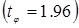и точности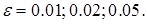

Ввиду того, что значения P до проведения эксперимента неизвестны, то вычисляют множество оценок N для диапазона возможных значений P, т.е. от 0 до 1 с дискретностью 0.1. Результаты расчетов с использованием выражения (4.78) представлены в таблице 4.17.

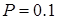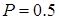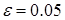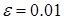Из таблицы 4.17 видно, что при переходе от (0.9) и количество реализаций N возрастает примерно в 2,5 раза, а при переходе от и количество реализаций возрастает примерно в 25 раз.

Таблица 4.17

Вероятность Р	Точность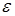
0.05	0.02	0.01
0.1 (0.9)
0.2 (0.8)
0.3 (0.7)
0.4 (0.6)
0.5 (0.5)

При тактическом планировании машинных экспериментов, когда значение P неизвестно, поступают следующим образом. Берут произвольно значение N₀, определяют по формуле 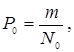а затем по формуле (4.78) проводят вычисления, в которой вместо P подставляют P₀. Такая процедура оценки N может выполняться многократно.

Если отсутствует возможность получения каких-либо априорных сведений о вероятности P, то в таких случаях целесообразно задавать относительную точность результатов моделирования .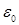

Для этих случаев формула (4.78) принимает вид

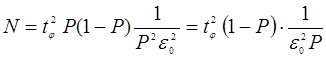(4.79)

Оценку показателя эффективности Е модулируемой системы можно дать по результатам определения среднего значения некоторой случайной величины. Если случайная величина x имеет математическое ожидание а и дисперсию s² и принимает в i -той реализации значение 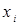, то в качестве оценки математического ожидания а принимают

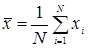
При больших значениях N в силу предельной центральной теоремы теории вероятностей среднее арифметическое 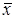будет иметь распределение, близкое к нормальному с математическим ожиданием а и дисперсией .

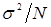Точность оценки для математического ожидания равна 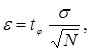а количество реализаций

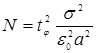(4.80)

Если же в качестве показателя эффективности Е выступает дисперсия s², а в качестве ее оценки используется выборочная дисперсия S², то математическое ожидание и дисперсия будут

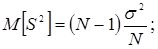
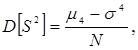
где 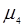– центральный момент четвертого порядка случайной величины.

Для частного случая, когда случайная величина имеет нормальное распределение, когда 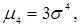получаем

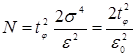(4.81)

Для дисперсии s² точность оценки

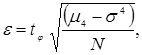
отсюда количество реализаций

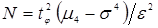или .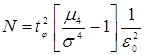

Из выражений (4.79¸4.81) видно, что количество реализаций существенно зависит от дисперсии оцениваемой случайной величины. Поэтому выгодно выбирать те оцениваемые показатели эффективности Е, которые имеют малые дисперсии.

Дата добавления: 2014-01-15