Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе

Самые слабые - номинальные шкалы, а самые сильные - абсолютные.
Выделяют три основных характеристики измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории:
1. Упорядоченность данных в измерительной шкале означает, что один элемент шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому элементу этой шкалы;

> Y_{j +1} (x_j+1)

Y_i (x_i) → } < Y_{j -1} (x_j-1)

= Y_j (x_j)

2. Интервальность элементов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел;

> Y_i+1 (x_i+1) - Y_j+1 (x_j+1)

[Y_j (x_j) - Y_i (x_i)] →} < Y_{j -1} (x_j-1) - Y_j-1 (x_j-1)

= Y_{j –I} (x_j-i) - Y_j-i (x_j-i)

3. Нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства (нет измеряемого свойства – нет измерения - нет обозначения).

Пример: годовой счет времени - летоисчисление

Выделяют следующие группы шкал:
- неметрические или качественные шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы);
- количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала).

Ниже представлена классификационная структура измерительных шкал.

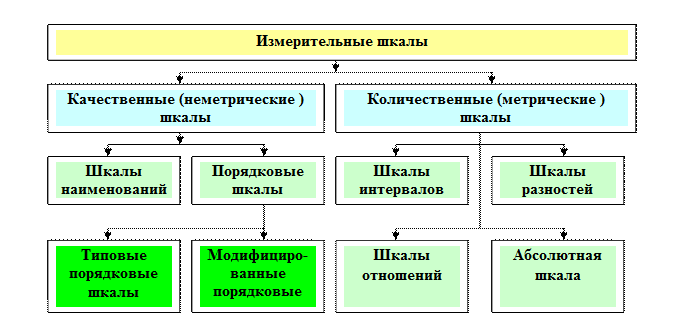
Рис.1 Классификация измерительных шкал

Виды шкал

- Шкалы номинального типа (шкалы наименований)

- Шкалы порядка (порядковые шкалы)

- Шкалы интервалов

- Шкалы отношений

- Шкалы разностей

- Абсолютные шкалы

Качественные шкалы

1. Шкала наименований
Шкала наименований (номинальная или классификационная) представляет собой конечный набор обозначений состояний (свойств) объекта, никак не связанных между собой (рис. 2).
Здесь отсутствуют все главные атрибуты измерительных шкал, а именно упорядоченность, интервальность, нулевая точка.

Рис. 1. Номинальная шкала.

Измерение будет состоять в том, чтобы, проведя эксперимент над объектом, определить принадлежность результата к тому или иному состоянию и записать это с помощью символа (набора символов), обозначающего данное состояние. Это самая простая шкала из тех, что могут рассматриваться как измерительные, хотя фактически эта шкала не ассоциируется с измерением и не связана с понятием «величина».

Она используется только с целью отличить один объект от другого.
Если классифицируются дискретные по своей природе объекты и явления, то естественнее всего использовать шкалу наименований.

Шкалы наименований - отражают качественные свойства. Их элементы характеризуются только соотношениями эквивалентности (равенства) и сходства конкретных качественных проявлений свойств.

Примеры:
Для обозначения в номинальной шкале могут быть использованы:
- слова естественного языка (например, географические названия, собственные имена людей и т. д.);
- произвольные символы (гербы и флаги государств, эмблемы родов войск, всевозможные значки и т. д.);
- номера (регистрационные номера автомобилей, официальных документов, номера на майках спортсменов);
- их различные комбинации (например, почтовые адреса, экслибрисы личных библиотек, печати и пр.)

- различные коллекции (марок, монет, картин и т.д.).
Однако необходимость классификации возникает и в тех случаях, когда классифицируемые состояния образуют непрерывное множество (или континуум).

Задача сводится к предыдущей, если все множество разбить на конечное число подмножеств, искусственно образуя тем самым классы эквивалентности; тогда принадлежность состояния к какому-либо классу снова можно регистрировать в шкале наименований. Однако условность введенных классов (не их шкальных обозначений, а самих классов) рано или поздно проявится на практике.
Примеры:
1. Например, возникают трудности точного перевода с одного языка на другой при описании цветовых оттенков: в английском языке голубой, лазоревый и синий цвета не различаются.
2. Названия болезней также образуют шкалу наименований. Психиатр, ставя больному диагноз «шизофрения», «паранойя», «маниакальная депрессия» или «психоневроз», использует номинальную шкалу; и все же иногда врачи не зря вспоминают, что «нужно лечить больного, а не болезнь»: название болезни лишь обозначает класс, внутри которого на самом деле имеются различия, так как эквивалентность внутри класса носит условный характер.
Необходимо понимать, что обозначения классов — это только символы, даже если для этого использованы номера. С этими номерами нельзя обращаться как с числами — это только цифры.
Пример. Если у одного спортсмена на спине номер 1, а другого — 2, то никаких других выводов, кроме того, что это разные участники соревнований, делать нельзя: например, нельзя сказать, что «второй в два раза лучше».
При обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию проверки их совпадения или несовпадения.

Примерами таких шкал еще является

шкала классификации (оценки) цвета объектов по наименованиям (красный, оранжевый, желтый, зеленый и т.д.), опирающаяся на стандартизованные атласы цветов, систематизированные по сходству. В таких атласах, выполняющих роль своеобразных эталонов, цвета могут обозначаться условными номерами (координатами цвета). Измерения в шкале цветов выполняются путем сравнения при определенном освещении образцов цвета из атласа с цветом исследуемого объекта и установления эквивалентности их цветов.

В шкале наименований допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются лишь как метки. Примерно так же, как при сдаче белья в прачечную, т.е. лишь для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Номера страховых свидетельств государственного пенсионного страхования, медицинского страхования, ИНН (индивидуальный номер налогоплательщика), штрих-коды товаров измерены в шкале наименований. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения - мужской, женский. Раса, национальность, цвет глаз, волос - номинальные признаки. Номера букв в алфавите - тоже измерения в шкале наименований. Никому в здравом уме не придет в голову складывать или умножать номера телефонов, такие операции не имеют смысла. Сравнивать буквы и говорить, например, что буква П лучше буквы С, также никто не будет. Единственное, для чего годятся результаты измерений в шкале наименований - для различения объектов.

В шкалах наименований нельзя ввести понятия единицы измерения; в них отсутствует и нулевой элемент.

Шкалы наименований, по существу, качественны; однако возможны некоторые статистические операции при обработке результатов измерений в этих шкалах, например, можно найти модальный или наиболее многочисленный класс эквивалентности.

2. Порядковые шкалы
Следующей по силе за номинальной шкалой идет порядковая, шкала (ординальная, ранговая). Она применяется в тех случаях, когда наблюдаемый (измеряемый) признак состояния имеет природу, не только позволяющую отождествить состояния с одним из классов эквивалентности, но и дающую возможность в каком-то отношении сравнивать разные классы.
Порядковая шкала не имеет определенной количественной меры. При этом присутствует упорядоченность, но отсутствуют атрибуты интервальности и нулевой точки.
Единственными типами отношений между неколичественными значениями шкалы могут быть:
а) равенство одинаковых значений порядковых переменных величин, соответствующих объектам одной категории,
б) неравенство разных значений переменных величин, соответствующих объектам одной категории;
в) отношения «больше» или «меньше» между разными значениями переменных величин, соответствующих объектам одной категории.
Измерение в шкале порядка может применяться, например, в следующих ситуациях:
- когда необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих объектов;
- когда нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение;
- когда какое-либо качество в принципе измеримо, но в настоящий момент не может быть измерено по причинам практического или теоретического характера.

В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся.Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно - неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается "нечисловой" характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго возрастающие преобразования.

2.1. Типовые порядковые шкалы

Обозначив такие классы символами и установив между этими символами отношения порядка, мы получим шкалу простого порядка: А → В → C → D → E → F.
Примеры:
Нумерация очередности, призовые места в конкурсе, социально-экономический статус («низший класс», «средний класс», «высший класс»).
Разновидностью шкалы простого порядка являются оппозиционные шкалы. Они образуются из пар антонимов (например, сильный-слабый), стоящих на разных концах шкалы, где за середину берется позиция, соответствующая среднему значению наблюдаемой сущности. Как правило, остальные позиции никак не шкалируются.
Иногда оказывается, что не каждую пару классов можно упорядочить по предпочтению: некоторые пары считаются равными — одновременно А ≥ В и В≤ А, т. е. А = В.
Шкала, соответствующая такому случаю, называется шкалой слабого порядка.
Иная ситуация возникает, когда имеются пары классов, несравнимые между собой, т. е. ни А≥ В, ни В ≤ А. В таком случае говорят о шкале частичного порядка. Шкалы частичного порядка часто возникают в социологических исследованиях субъективных предпочтений. Например, при изучении покупательского спроса субъект часто не в состоянии оценить, какой именно из двух разнородных товаров ему больше нравится (например, клетчатые носки или фруктовые консервы, велосипед или магнитофон и т. д.); затрудняется человек и упорядочить по предпочтению любимые занятия (чтение литературы, плавание, вкусная еда, слушание музыки).
Характерной особенностью порядковых шкал является то, что отношение порядканичего не говорит о дистанции между сравниваемыми классами. Поэтому порядковые экспериментальные данные, даже если они изображены цифрами, нельзя рассматривать как числа..
Пример.

Рассматривается испытание умственных способностей группы людей, при котором измеряется время, затрачиваемое испытуемым на решение тестовой задачи. В таких экспериментах время хотя и измеряется в числовой шкале, но как мера интеллекта принадлежит порядковой шкале.
Порядковые шкалы определяются только для заданного набора сравниваемых объектов, у этих шкал нет общепринятого, а тем более абсолютного стандарта.
Примеры:
1. При определенных условиях правомерно выражение «первый в мире, второй в Европе» - просто чемпион мира занял второе место на европейских соревнованиях.
2. Само расположение шкал является примером порядковой шкалы.

Дата добавления: 2014-01-15