КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условия энтропии и ее свойства
|
|
|
|
Подключение к компьютеру поставщика услуг Интернет
Браузеры
Поисковые системы
Некоторые географические домены 1 уровня
fr - Франция
de - Германия
ru - Россия
se - Швеция
tm – Туркменистан
Принцип действия поисковых систем напоминает работу обычных баз данных. Вы вводите какой-то запрос, например набор ключевых слов и в результате получаете список документов содержащих заданные слова. Отличие заключается в способе наполнения такой «базы». Для этого в поисковых системах используется периодическое сканирование содержимого серверов с помощью специальных программ – роботов. На основе деятельности этих специальных программ составляются файлы-индексы, которые имеют огромные размеры и используются для поиска задаваемых вами ключевых слов. Помимо простого запроса обычно существует возможность указания различных логических операций, логических групп, использования шаблонов, поиска в названиях, заголовках, задания расстояний между словами.
Отображение информации происходит посредством специальной программы – браузера. Браузер может быть графическим или текстовым. Для того чтобы браузеры могли интерпретировать документы, они должны быть оформлены специальным образом – размечены в соответствии со спецификацией языка HTML. В основе языка HTML версии 1.2 лежала логическая разметка, это позволят текстовым браузерам выделять заголовки либо строчными буквами, либо пустыми строками сверху и снизу.
Для подключения к компьютеру поставщика услуг Интернет надо правильно настроить программу Удаленный доступ к сети. При настройке программы необходимы данные, которые должен сообщить поставщик услуг:
· номер соединения, по которому производится соединение;
· имя пользователя (login);
· пароль (password);
· IP-адрес сервера DNS.
Определим энтропию двух статистически связанных ансамблей U и V. Объединение ансамблей характеризуется матрицей P (UV) вероятностей P (u i v j) всех возможных комбинаций состояний 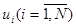 ансамбля U и
ансамбля U и 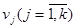 ансамбля V:
ансамбля V:
 (11)
(11)
Суммируя столбцы и строки матрицы (11) получим информацию об ансамблях U и V исходных источников u и v:

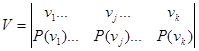
Вероятности P (u i v j) совместной реализации равны
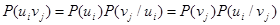 (12)
(12)
где 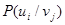 и
и  - условные вероятности:
- условные вероятности:
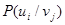 - вероятность реализации состояний u i ансамбля U при условии, что реализовалось состояние v j ансамбля V,
- вероятность реализации состояний u i ансамбля U при условии, что реализовалось состояние v j ансамбля V,  - определяется аналогично. Тогда выражение (8) для энтропии объединения принимает вид
- определяется аналогично. Тогда выражение (8) для энтропии объединения принимает вид
 (13)
(13)
Обозначим и назовем сумму
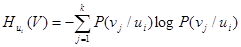 (14)
(14)
частной условной энтропией ансамбля. Оно представляет собой случайную величину, характеризующую неопределенность, приходящуюся на одно состояние ансамбля V при условии, что реализовалось конкретное состояние u i ансамбля U.
При усреднении по всем состояниям ансамбля U получаем среднюю неопределенность, приходящуюся на одно состояние ансамбля V при известных состояниях ансамбля U:
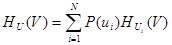 (15)
(15)
или

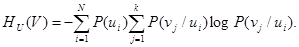 (16)
(16)
Величину H U(V) называют полной условной или просто условной энтропией ансамбля V по отношению к ансамблю U. 
Подставляя(16) в (13) получим
 (17)
(17)
Выражая в (8) P (u i v j)через другую условную вероятность в соответствии с (12), найдем
 (18)
(18)
где
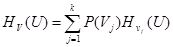 (19)
(19)
и
 (20)
(20)
Т.о. энтропия объединения двух статистически связанных ансамблей U и V равна безусловной энтропии одного ансамбля условная энтропия другого относительно первого.
Распространяя правило (17) на объединение любого числа зависимых ансамблей, получим
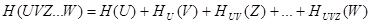 (21)
(21)
В объединении ансамблей и условная энтропия любого ансамбля всегда меньше или равна безусловной энтропии этого же ансамбля.
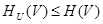 (22)
(22)
 (очевидно) (23)
(очевидно) (23)
Тогда
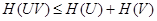 (24)
(24)
Для нескольких ансамблей
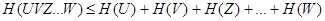 (25)
(25)
Наличие сведений о результатах реализации состояний одного ансамбля никак не может увеличить неопределенность выбора состояния из другого ансамбля. Эта неопределенность может только уменьшаться, если существует связь в реализациях состояний из обоих ансамблей.
В случае отсутствия статистической связи

 (26)
(26)
Если связь однозначна, то

 (27)
(27)
т.к. условные вероятности 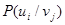 и
и  в этом случае принимают значения равные нулю или единице.
в этом случае принимают значения равные нулю или единице.
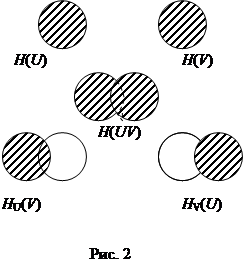
Уяснению соотношений между рассмотренными энтропиями дискретных источников информации (ансамблей) способствует их графическое отображение (рис. 2).
 |
ЛЕКЦИЯ 12
Количество информации как мера снятой неопределенности.
Передача информации диктуется желанием устранить неопределенность относительно последовательности состояний, реализуемых некоторым источником информации.
Информация проявляется всегда в форме сигналов. Сигналы Z, поступающие с выхода первичного преобразователя источника информации на вход сигнала связи, принято называть сообщениями в отличие от сигнала “ u ”, формирующегося на входе линии связи.
Отдельные первичные сигналы с выхода источника дискретных сообщений называют элементами сообщений. Каждому элементу сообщения соответствует определенное состояние источника информации.
Основное понятие теории информации – количество информации – рассмотрим применительно к передаче отдельных статистически несвязанных элементов сообщения. Дискретный источник сообщений при этом полностью характеризуется ансамблем

Передача информации от дискретного источника.
Выясним на сколько изменится неопределенность относительно состояния источника сообщения при получении адресатом элемента сообщения с выхода канала связи. Алфавиты передаваемых и принимаемых элементов сообщений считаем идентичными.
Вследствие воздействия помех полученный (сигнал) элемент сообщения в общем отличается от переданного, поэтому принимаемые элементы сообщения обозначим другими буквами: w 1, w 2, …, w i, …, w N.
Априорная неопределенность (неопределенность до получения элемента сообщения) относительно источника сообщений не является полной. Предполагается, сто адресату известен алфавит элементов сообщения, а из прошлого опыта он знает вероятности их появления. Считая, что состояние источника реализуется независимо, априорная частотная неопределенность появления элемента сообщения Z i
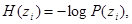
где  априорная вероятность появления элемента сообщения Z i.
априорная вероятность появления элемента сообщения Z i.
Предполагаются также известными некоторые сведения относительно помехи в канале связи. Обычно считают, что между элементами сообщения и помехой статистические связи отсутствуют, искажения отдельных элементов сообщения являются событиями независимыми и адресату известна совокупность условных вероятностей 
 того, что вместо элемента сообщения Z i будет принят сигнал w j, т.е., что при получении сообщения w j исходной его причиной была передача сообщения Z i.
того, что вместо элемента сообщения Z i будет принят сигнал w j, т.е., что при получении сообщения w j исходной его причиной была передача сообщения Z i.
При получении w j адресату становится известно значение условной вероятности  , называемой апостериорной вероятностью реализации источником элемента сообщения Z i. Это позволяет найти апостериорную частную неопределенность, остающуюся у адресата относительно выдачи источников элемента сообщения w j
, называемой апостериорной вероятностью реализации источником элемента сообщения Z i. Это позволяет найти апостериорную частную неопределенность, остающуюся у адресата относительно выдачи источников элемента сообщения w j

 (28)
(28)
Поскольку получение информации связывается с уменьшением неопределенности, естественно определить частное количество информации I (Z i), получаемое при приеме элемента сообщения w j относительно реализованного источником элемента сообщения Z i, как разность частных неопределенностей, имевшихся у адресата до и после получения элемента сообщения (априорной и апостериорной)
 (29)
(29)
Анализ (29) показывает
1. Частное количество информации растет с уменьшением априорной увеличением апостериорной вероятностей реализации элемента сообщения источником.
2. Частное количество информации может быть как положительным, так и отрицательным, а так же нулем. Если вероятность реализации источником элементов сообщения Z i увеличилась после приема элемента сообщения w j, т.е. 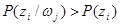 , то полученное количество информации положительно. Если эта вероятность не изменилась, т.е.
, то полученное количество информации положительно. Если эта вероятность не изменилась, т.е. 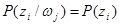 , то имевшая место неопределенность тоже не изменилась и I (z i)=0. Cлучай
, то имевшая место неопределенность тоже не изменилась и I (z i)=0. Cлучай  соответствует увеличению неопределенности относительно реализации Z i после получения элемента сообщения w j и, следовательно, частое количество информации отрицательно, т.е. величина дезинформации, внесенной помехами, превышает величину информации, которую несет переданное сообщение.
соответствует увеличению неопределенности относительно реализации Z i после получения элемента сообщения w j и, следовательно, частое количество информации отрицательно, т.е. величина дезинформации, внесенной помехами, превышает величину информации, которую несет переданное сообщение.
3. В случае отсутствия помехи апостериорная вероятность 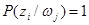 . При этом частное количество информации численно совпадают с частной априорной неопределенностью реализации данного элементе сообщения Z i:
. При этом частное количество информации численно совпадают с частной априорной неопределенностью реализации данного элементе сообщения Z i:

Это максимальное частное количество информации, которое можно получить от элементов сообщения Z i;
4. Частное количество информации относительно реализации источником элемента сообщения Z i, содержащееся в элементе сообщения w j, равно частному количеству информации относительно w j, содержащемуся в элементе сообщения Z i.
По теории Байеса вероятность совместного поступления событий Z i и w j
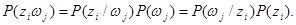
Разделив все части уравнения на произведение  имеем
имеем

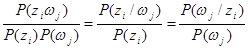
Поэтому можно записать
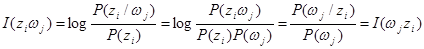 (30)
(30)
Найдем среднее количество информации, содержащееся в любом принятом элементе сообщений относительно переданного (реализованного) источником. До получения конкретного элемента сообщения средняя неопределенность, имеющаяся у адресата, относительно реализации источником любого элемента сообщения равна энтропии источника. Ее называют априорной энтропией источника.
Средняя неопределенность относительно любого состояния источника, остающаяся у адресата после получения конкретного элемента сообщения w j, характеризуется частной условной энтропией H w j ( z ):
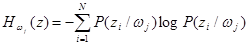 (31)
(31)
Это случайная величина, зависящая от того, какой конкретно элемент принят.
Средняя неопределенность по всему ансамблю принимаемых элементов сообщений равна условной энтропии источника H W(Z):
 (32)
(32)
Эту энтропию называют апостериорной энтропией источника информации.
Таким образом, при наличии помех среднее количество информации, содержащееся в каждом принятом элементе сообщения, относительно любого переданного равно разности априорной и апостериорной энтропий источника:
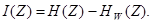 (33)
(33)
Подставив выражения H (Z) и H W(Z) из (6) и (32) в (33) и проведя несложные преобразования, получим формулу для количества информации непосредственно через вероятности:



(34)

Справка. Учитывая, что сумма условных вероятностей P (z i/ w j) отвечает условию нормирования, т.е. 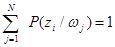 , можем записать:
, можем записать:

|

В общем случае H W(z) есть величина дезинформации вносимой помехами (шумами).
Можно показать, что справедливо и другое выражение
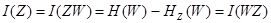 (35)
(35)
Доказано, что  , т.е. среднее количество информации не может быть отрицательным.
, т.е. среднее количество информации не может быть отрицательным.
При подсчете количества информации удобно применение двоичных логарифмов. Пусть объект имеет два возможных состояния. Тогда для передачи сообщений о состоянии объекта можно применить элементарный двухпозиционный сигнал. Если вероятности обоих состояний объекта равны между собой, т.е. P i=1/2, то при пользовании двоичными логарифмами энтропия источника H (Z)=1. Этой же величине равно количество информации I, если в канале нет помех. В данном случае один элементарный сигнал несет одну двоичную единицу информации.
С помощью k элементарных двоичных сигналов можно передать сообщение об объекте, имеющем 2k возможных состояний. Если все эти состояния равновероятны, то каждое сообщение из k символов имеет количество информации, равное k двоичным единицам. Этим объясняется удобство применения двоичных логарифмов. Двоичная единица информации называется битой.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1210; Нарушение авторских прав?; Мы поможем в написании вашей работы!