Паутинообразная модель 1

Экономические модели

Существует много различных вариантов фирм, но все они обладают определенными сходными свойствами. [4,10] Обычно в них предполагается, что спрос на некоторый продукт на заданном отрезке времени зависит от его цены (и других факторов) на этом отрезке. Что касается предложения, то оно определяется ценами предыдущего периода времени. И далее считают, что рынок всегда находится в условиях локального равновесия. Одна из разновидностей экономических моделей является паутинообразная, представляющая собой простейшую динамическую модель взаимодействия фирмы и рынка.

Представляет из себя вероятностную модель. Условия локального равновесия рынка в вероятностной модели описывается следующим уравнением:

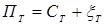(5.1)

где: 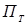- предложение на Т -ом отрезке времени; 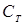- спрос на Т -ом отрезке времени; 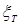- случайная величина с заданным законом распределения с математическим ожиданием 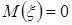и дисперсией .

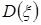Уравнение функционирования фирмы имеют вид:

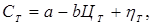(5.2)

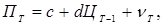(5.3)

где: 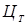- цена на Т -ом отрезке времени; 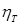- случайная величина с заданным законом распределения с математическим ожиданием 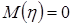и дисперсией 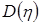; 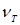- случайная величина с заданным законом распределения с математическим ожиданием 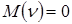и дисперсией 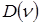; 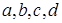- константы, которые определяются с помощью стандартных эконометрических методов.

Из формулы (5.2) видно, что спрос 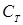на Т -ом отрезке времени линейно зависит от текущей цены и случайной величины 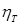, которая характеризует непредвиденные колебания предпочтений и доходов потребителей, а также другие случайные факторы, влияющие на величину спроса.

Уравнение (5.3) также является линейным: предложение 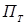на Т -ом отрезке времени зависит от цены на (Т-1) -ом отрезке времени и от значения случайной величины 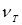. Здесь случайная величина может быть обусловлена погодой, если рассматривается сельскохозяйственная продукция, или от колебания технологии, от эффективности производственного процесса и т.д. (даже от политических нюансов).

Условие локального равновесия рынка означает совпадение спроса и предложение с точностью до случайной величины .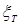

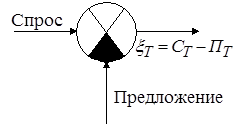
Рис. 5.1. Условие локального равновесия рынка

Подставим выражение 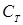и 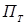в (5.1) и разрешим уравнение относительно :

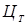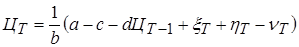(5.4)

Это отношение с учетом заданного начального значения цены 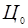и законов распределения случайных величин 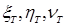может быть принята как имитационная модель. На ЭВМ с помощью прогонов можно получить траектории переменных ,,.

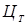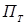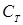Блок-схему имитационной модели можно представить в следующем виде:

Предположим, что в идеальном случае

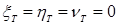
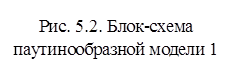В этом случае вид траектории 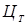полностью определяется соотношением параметров 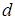и 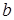. В зависимости от этого отношение колебания цены 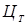могут быть раскачивающимися, с постоянной амплитудой или затухающими:

- если 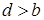, амплитуда колебаний неограниченно растет;

- если 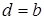, колебания имеют постоянную амплитуду;

- если 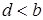, колебания затухают.

Дата добавления: 2014-01-15