Введение в теорию нелинейных систем

Лекция 12

Вопросы и задачи для самопроверки

1. Как определяется статический и дифференциальный параметр нелинейных элементов.

2. Нарисовать вольт-амперную характеристику в одной из точек которой статическое и дифференциальное сопротивление одинаково.

3. Объяснить принцип действия мостового выпрямителя и выпрямителя с выводом средней точки трансформатора.

4. Объяснить принцип построения эквивалентных схем нелинейной катушки и конденсатора.

Система называется (является) линейной, если для неё выполняется принцип суперпозиции, а именно, линейной комбинации любых входных воздействий соответствует та же линейная комбинация соответствующих выходных функций:

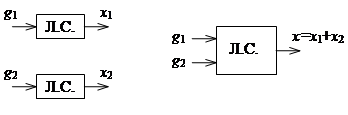
Системы, для которых принцип суперпозиции не выполняется, называются нелинейными. Динамические процессы в нелинейных системах, как правило, разнообразнее и сложнее процессов в линейных системах.

Что характерно для линейных систем?

Общее решение уравнения линейного дифференциального уравнения движения

,

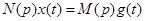описывающего динамику линейной системы, представляет собой сумму свободного (собственного) и частного вынужденного движений

,

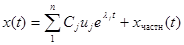где

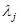- собственные числа, определяемые только параметрами системы,

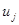- собственные векторы, определяемые параметрами системы,

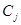- коэффициенты, определяемые начальными условиями,

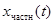- частное решение неоднородного уравнения (вынужденное движение).

Собственные движения линейных систем характерны тем, что

- вид движений системы (гармонические колебания, затухающие колебания, расходящиеся колебания, апериодический процесс), определяемый величинам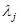и и 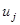, зависит только от параметров системы (коэффициентов уравнений движения);

- изменение начальных условий, определяющих величины С_j, приводит только к количественным изменениям в движении, без изменения его вида;

- чисто колебательное движение (т.е. нахождение на границе устойчивости) за счёт небольшого изменения параметров системы превращается либо в сходящийся, либо расходящийся процесс;

- резонанс возможен только на частоте периодического входного воздействия,

- точность, устойчивость и качество переходных процессов не зависит от величины внешнего воздействия. Изменение величины входного воздействия вызывает только пропорциональное изменение выходной величины, не изменяя характера движения.

Вынужденные движения линейных систем характерны тем, что в силу принципа суперпозиции реакция системы на произвольное внешнее воздействие (возмущение) g (t) может быть выражена через реакции системы на определённый вид элементарных возмущений, из которых складывается возмущение g (t). Иными словами, любая линейная система полностью характеризуется её реакцией на какой-нибудь стандартный тип возмущений.

Например, если 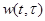- весовая функция, то

.

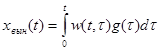В зависимости от выбора стандартного входного воздействия мы получаем разные характеристики линейной системы. Каждая из этих характеристик будет исчерпывающей, т.к. знание её достаточно для нахождения реакции системы на любое возмущение.

Дата добавления: 2014-01-15