Логические операции

Элементы математической логики

Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно в данный момент времени.

Пример

1. Курица – птица. – высказывание

2. Пейте томатный сок. – не высказывание.

В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний. Истинностные значения – истина и ложь – будем обозначать И и Л соответственно. Множество {И, Л} называется множеством истинностных значений.

Высказывание называют простым (элементарным), если оно рассматривается как неделимое целое (аналогично элементу множества). Сложным (составным) называется высказывание, составленное из простых с помощью логических связок.

Рассмотрим логические операции (связки) над высказываниями.

Отрицанием высказывания называется новое высказывание, истинное только тогда, когда исходное высказывание ложно.

Отрицание определяется следующей таблицей истинности.

№ набора	a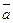
0	0	1
1	1	0

Отрицание обозначается через 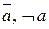и читается как «не а», «неверно, что а».

Конъюнкцией двух высказываний называется новое высказывание, которое истинно только тогда, когда оба исходных высказывания истинны.

№ набора	a	b	aÙb
0	0	0	0
1	0	1	0
2	1	0	0
3	1	1	1

Конъюнкция обозначается 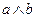или a&b или 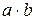или ab и читается как «a и b», «a, но b», «a, а b».

Дизъюнкцией двух высказываний называется новое высказывание, которое ложно только тогда, когда оба исходных высказывания ложны.

№ набора	a	b	aÚb
0	0	0	0
1	0	1	1
2	1	0	1
3	1	1	1

Дизъюнкция обозначается через 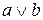или 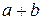и читается как «a или b».

Импликацией двух высказываний называется новое высказывание, которое ложно только тогда, когда первое истинно, а второе – ложно.

№ набора	a	b	a®b
0	0	0	1
1	0	1	1
2	1	0	0
3	1	1	1

Импликация обозначается a® b или aÉb и читается как «если a, то b»; «из а следует b». При этом a называется посылкой (условием), b – следствием (заключением).

Эквиваленцией (или эквивалентностью) двух высказываний является новое высказывание, которое считается истинным, когда оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.

№ набора	a	b	a»b
0	0	0	1
1	0	1	0
2	1	0	0
3	1	1	1

Эквивалентность обозначается a» b или a «b и читается как «a эквивалентно b»; а тогда и только тогда, когда b.

Приоритет операций:

Ø, Ù, Ú, ®, ~

Область действия логической связки определяется частью формулы, ограниченной скобками, между которыми находится данная связка.

Введем в рассмотрение еще три операции: сумма по модулю два (Å), штрих Шеффера (ï), стрелка Пирса (¯). Для них таблица истинности имеет следующий вид:

№ набора	a	b	aÅb	aïb	a¯b
0	0	0	0	1	1
1	0	1	1	1	0
2	1	0	1	1	0
3	1	1	0	0	0

Дата добавления: 2014-01-15