Формулы логики высказываний

Алфавитом называется любое непустое множество. Элементы этого множества называются символами данного алфавита. Словом в данном алфавите называется произвольная конечная последовательность символов (возможно пустая).

Алфавит логики высказываний содержит следующие символы:

· высказывательные переменные;

· логические символы;

· символы скобок.

Слово в алфавите логики высказываний называется формулой, если оно удовлетворяет следующему определению:

1) любая высказывательная переменная – формула;

2) если А и В – формулы, то Ø А, А Ù В, АÚ В, А® В, АÅ В, А»В, А ï В, А ¯ В – формулы;

3) только те слова являются формулами, для которых это следует из 1) и 2).

Подформулой формулы А называется любая ее часть, которая сама является формулой.

Примеры

1) «Завтра будет снег или дождь».

Высказывание состоит из двух простых, соединенных связкой «или»:

а – «завтра будет снег»;

b – «завтра будет дождь».

Логическая формула имеет вид: аÚb.

2) «Сегодня понедельник или вторник» состоит из двух простых:

а – «сегодня понедельник»;

b – «сегодня вторник».

Т.к. одновременное выполнение условий не допускается, то данное высказывание представимо логической формулой: a Å b.

Формула называется выполнимой (опровержимой), если существует такой набор значений переменных, при которых эта формула принимает значение 1 (0).

Формула называется тождественно-истинной, или тавтологией (тождественно-ложной или противоречием), если эта формула принимает значение 1 (0) при всех наборах значений переменных.

Только И	Хотя бы одна И и хотя бы одна Л	Только Л
общезначимая	нейтральная	невыполнимая
общезначимая	необщезначимая
выполнимая	невыполнимая

Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу переменных. Равносильность формул обозначается A º B.

Рассмотрим основные равносильности логики высказываний.

1. Идемпотентность
А Ù А = А	А Ú А = А
2. Коммутативность
А Ù В = В Ù А	А Ú В = В Ú А
3. Ассоциативность
А Ù (В Ù С) = (А Ù В) Ù С	А Ú (В Ú С) = (А Ú В) Ú С
4. Правила поглощения
А Ù (А Ú В) = А	А Ú (А Ù В) = А
5. Дистрибутивность
А Ù (В Ú С) = (А Ù В) Ú (А Ù С)	А Ú (В Ù С) = (А Ú В) Ù (А Ú С)
6. Правила де Моргана
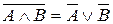
7. Свойства констант
А Ù 1 = А А Ù 0 = 0	А Ú 0 = А А Ú 1 = 1
8. Закон исключения третьего и закон противоречия
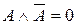
9. Снятие двойного отрицания
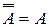
10. Формулы расщепления (склеивания)
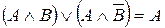
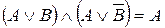
11. Связь дизъюнкции, конъюнкции, отрицания и импликации
12. Выражение эквивалентности

Любая из этих равносильностей легко может быть доказана с помощью таблицы истинности.

Пример.

Рассмотрим правило поглощения А Ù (А Ú В) = А.

А	В	АÚВ	АÙ(АÚВ)

Результирующий столбец и столбец А совпадают на все наборах. Значит формулы равносильны.

Часто для доказательства равносильностей формул используют приведенные выше равносильности.

Пример

Утверждение. Каждой формуле логики высказываний соответствует некоторая булева функция.

Дата добавления: 2014-01-15