Опуклість і вгнутість кривої. Точка перегину

Означення. Крива на проміжку називається опуклою (угнутою), якщо всі точки кривої лежать нижче (вище) будь-якої її дотичної на цьому проміжку.

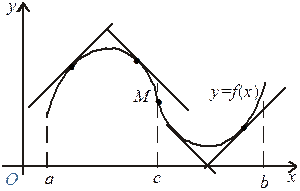
З графіка функції , який показано на малюнку бачимо: крива є опуклою на проміжку (а, с) і вгнутою на проміжку (с, b).

Означення. Точка, яка відокремлює опуклу частину кривої від вгнутої, називається точкою перегину.

На малюнку графіка функції, що наведено раніше, точка М — точка перегину.

Розглянемо дві теореми.

Теорема 1. 1) Якщо в усіх точках проміжку (с, b) для функ­ції 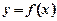друга її похідна додатна , то графік функ­ції вгнутий.

2) Якщо в усіх точках проміжку (а, с) друга похідна від’єм­на , то графік функції випуклий.

Теорема 2. Якщо для функції 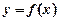друга похідна її у деякій точці х ₀ перетворюється на нуль або не існує й при переході через цю точку змінює свій знак на обернений, то точка 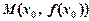є точкою перегину графіка функції.

Зауваження. Якщо у точці х ₀ друга похідна дорівнює нулю або не існує, але при переході через цю точку не змінює свого знака, то точка не є точкою перегину.

Приклад. Знайти інтервали опуклості та вгнутості графіка функції .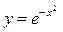

Маємо .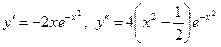

Друга похідна 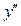перетворюється в нуль, коли

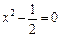, звідки .

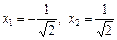При переході через точки х ₁ і х ₂ друга похідна змінює знак.

Таким чином, точки 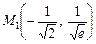і 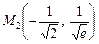є точками перегину графіка функції.

Результати дослідження заносимо в таблицю:

х
	+		–		+
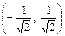
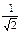
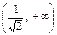
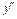
у	È	Перегин	Ç	Перегин	È

Із цієї таблиці бачимо, що графік функції на інтервалах і вгнутий, а на інтервалі 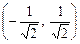— опуклий.

Дата добавления: 2014-01-15