Степень статической неопределимости

Разность между числом неизвестных, необходимых для расчёта заданного сооружения, и числом независимых уравнений равновесия, составленных для решения задачи, называется степенью статической неопределимости сооружения. Другими словами, эта разность определяет количество лишних связей в заданной расчётной схеме сооружения, усилия в которых требуется определить, не прибегая к уравнениям равновесия.

Степень статической неопределимости можно вычислить, преобразуя заданную статически неопределимую систему в статически определимую и параллельно подсчитывая число удалённых связей. Такой подход является наиболее общим, но часто у читателей вызывает определённые трудности. Поэтому в плоских стержневых системах на начальном этапе изучения этой и последующих тем степень статической неопределимости рекомендуется определять по формуле "контуров".

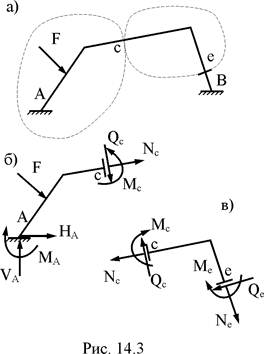Любой замкнутый плоский стержневой контур содержит три лишних связи, т.е. трижды статически неопределим. В этом можно убедиться, рассматривая определение внутренних усилий в сечении "с" рамы, представляющей собой вместе с диском "земля" замкнутый контур (рис. 14.3,а). Любая отсечённая часть этой рамы имеет шесть неизвестных: рис. 14.3,б – внутренние усилия в сечении "с" M_c, Q_c, N_c и реакции заделки V_A, H_A, M_A; рис. 14.3,в – внутренние усилия в сечениях "с" и "е" M_c, Q_c, N_c, M_е, Q_е, N_е. Равновесие рассматриваемых выше отсечённых частей описывается тремя уравнениями. Таким образом, разность между числом неизвестных, необходимых для описания напряжённо-деформированного состояния рамы, и числом уравнений равновесия равно трём.

Если сооружение состоит из К не накладывающихся друг на друга контуров, то общее число лишних связей в нём равно 3К.

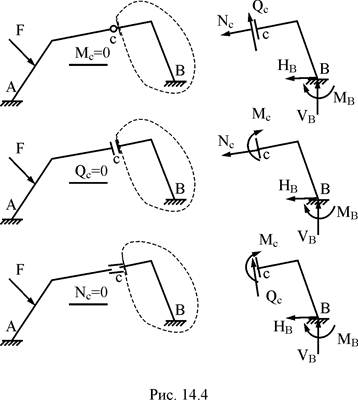
Наличие в одноконтурном сооружении одного простого цилиндрического или поступательного шарнира снижает степень статической неопределимости такого сооружения на единицу, так как любая отсечённая часть контура, включающая в себя сечение, расположенное на бесконечно близком расстоянии от шарнира, будет содержать теперь пять, а не шесть, неизвестных (рис. 14.4). Напомним читателям, что простой цилиндрический или поступательный шарнир связывает только два диска. Если шарнир соединяет n дисков, то он эквивалентен n–1 простому шарниру (см. п. 2.3 части 1 настоящего курса лекций).

В общем случае, если К контуров имеют Н простых цилиндрических или поступательных шарниров, то степень статической неопределимости сооружения равна

n_st = 3K – H. (14.1)

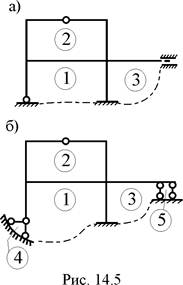
Число контуров и простых шарниров зависит от способа представления расчётной схемы сооружения. На рис. 14.5,а,б показано изображение расчётной схемы одной и той же рамы с различным количеством контуров и простых шарниров. Естественно, что степень статической неопределимости рамы не зависит от способа изображения её расчётной схемы. Действительно:

n_st = 3 × 3 – 3 = 6 (рис. 14.5,а),

n_st = 3 × 5 – 9 = 6 (рис. 14.5,б).

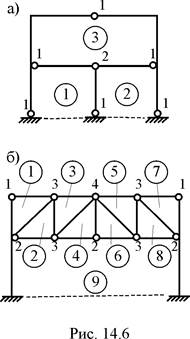
Пример 14.2.1. Используя формулу "контуров", вычислить степень статической неопределимости плоских стержневых систем, изображённых на рис. 14.6.

На рис. 14.6,а,б цифрами, объединёнными кружками, пронумерованы замкнутые контуры. Рядом с цилиндрическими шарнирами цифрами помечено количество простых шарниров.

n_st = 3 × 3 – 8 = 1 (рис. 14.6,а),

n_st = 3 × 9 – 24 = 3 (рис. 14.6,б).

14.3. Методы расчёта статически неопределимых систем

Для расчёта статически неопределимых систем используются следующие методы:

1. Метод сил.

2. Метод перемещений.

3. Комбинированный метод расчёта симметричных систем.

4. Смешанный метод.

5. Метод конечных элементов.

6. Приближённые методы (метод последовательных приближений и др.).

Подробное изложение сути этих методов дано ниже в настоящем (метод сил) и последующих изданиях лекций (остальные методы).

Дата добавления: 2014-01-15