Прямая в пространстве

Каноническое, параметрическое и векторное уравнения прямой.

Прямая l в про­странстве однозначно определяется заданием точки 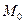, принад­лежащей l, и ненулевого вектора 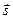, параллельного этой прямой. Вектор 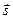называется направляющим вектором прямой l ( рис. 15.1 ).

рис. 15.1

Введем декартову систему координат и обозначим ко­ординаты точки 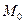через 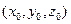, а координаты вектора 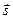через (m, n, p).

Для того, чтобы произвольная точка М(x,у,z) принадлежала прямой l, необходимо и достаточно, чтобы векторы 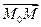и 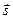были коллинеарными

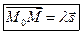(15.1)

Заметим, что для любого числа 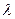, всякая точка М, удовлет­воряющая условию (15.1), принадлежит прямой l. Векторное равенство (15.1) равносильно трем скалярным равенствам:

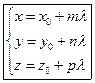. (15.2)

Эти уравнения называются параметрическими уравнениями прямой.

Если каждая из координат m, n, p вектора 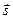отлична от нуля, то, исключая из системы (15.2) неизвестное 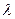, получим каноническое уравнение прямой

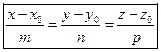. (15.3)

Если обозначить через 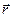и 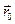радиус-векторы точек М и 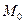соответственно, то равенство (15.3) можно записать в виде

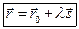(15.4)

Это уравнение называется векторным уравнением прямой l.

Замечание. Каноническое уравнение прямой получены при условии, что каждое из чисел m, n, p отлично от нуля. Однако в учебной литературе принято писать уравнение пря­мой в каноническом виде и в том случае, когда некоторые из чисел равны нулю. Эту запись не следует понимать как деление на нуль. Например, запись

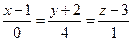
означает .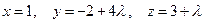

15.2 Общее уравнение прямой.

Рассмотрим систему ли­нейных уравнений

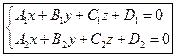(15.5)

Каждое из уравнений этой системы задает плоскость. Если эти плоскости пересекаются, то система (15.5) задает прямую - линию пересечения этих плоскостей. Условием пересечения плоскостей является непропорциональность коэффициентов при неизвестных. Таким образом, система (15.5) при условии непропорциональности коэффициентов задает прямую. Эти уравнения называются общим уравнением прямой.

Канонические уравнения прямой являют­ся частным случаем общих уравнений. Для этого достаточно записать канонические уравнения (15.3) в виде:

,

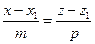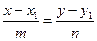
Каждое из уравнений системы задает плоскость, поскольку является уравнением первой степени. Особенность этих плоскостей состоит в том, что одна из них параллельна оси Оу, а другая — оси Oz.

Дата добавления: 2014-01-15